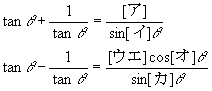
であり, これらを用いて tan 15° を求めると
tan 15° = [キ] - √[ク]
である。
第一問 (必答 30 点)
[1] (1) 0° < θ < 90° とする。
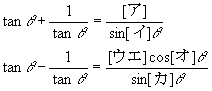
であり, これらを用いて tan 15° を求めると
tan 15° = [キ] - √[ク]
である。
(2) θ が 15° ≦ θ ≦ 60° の範囲を動くとき, tan θ + 1/tan θ
は
θ = [ケコ]° のとき最小値 [サ],
θ = [シス]° のとき最小値 [セ]
をとる。
[2] 方程式 ![]() の解 x を求めよう。
の解 x を求めよう。
![]() ………………
①
………………
①
と置くと, X の方程式
[ソ]X2 + [タ]X - 1 = 0
が得られる。
一方, ① より X > [チ] である。 従って X = [ツ]/[テ]
を得る。 これから求める x は x = [ト] log2[ナ]
となる。
第二問 (必答 30 点)
[1] 座標平面に於いて放物線 y = x2 を C とする。 第一象限の点 P(a, a2) における C の接線 l と y 軸との交点 Q の座標は (0, [ア]a[イ]) である。 l と y 軸の成す角が 30° となるのは a = (√[ウ])/[エ] のときである。 このとき線分 PQ の長さは √[オ] であり, Q を中心とし線分 PQ を半径とする円と放物線 C とで囲まれてできる二つの図形のうち小さい方の面積は π/[カ] - (√[キ])/[ク] である。
[2] 函数 y = 3sin θ - 2sin3 θ (0° ≦ θ
≦ 210°) の最大値と最小値を求めたい。 そのため sin θ = x
と置くと, y は
y = 3x - 2x3
と表される。 x の動く範囲は [ケコ]/[サ] ≦ x ≦ [シ]
であるから, y は x = 1/√[ス] のとき最大値 √[セ] をとり, x =
[ソタ]/[チ] のとき最小値 [ツテ]/[ト] をとる。
θ の函数としては, y は θ = [ナニ]° 及び [ヌネノ]° のとき最大, θ = [ハヒフ]° のとき最小である。
以下の第三問から第六問までは選択問題である。 2 問のみ選択して答えること。
第三問 (選択 20 点)
HP 管理者の注: 本問ではベクトルを太字の斜体で表している。
四面体の四つの頂点を O, L, M, N とする。 線分 OL を 2 : 1 に内分する点を P とし, 線分 MN の中点を Q とする。 a と b を 1 より小さい正の実数とする。 線分 ON を a : (1 - a) に内分する点を R とし, 線分 LM を b : (1 - b) に内分する点を S とする。 l = OL, m = OM, n = ON と置く。
(1) RS = ([ア] - [イ])l + [ウ]m
- [エ]n
RP = ([オ]/[カ])l - [キ]n
RQ = ([ク]/[ケ])m + ([コ]/[サ] - [シ])n
が成立する。
(2) 以下 l = (1, 0, 0), m = (0, 1, 0), n = (0, 0, 1) の場合を考える。
点 S が三点 P, Q, R の定める平面上にあるとする。
このとき, RS は実数 x, y を用いて RS = xRP
+ y RQ と表せる。 これより
x = ([ス]/[セ])(1 - b), y = [ソ]b
となり, a と b は
[タチ] + [ツ] - [テト] = 0
を満たすことが分かる。 更に, RP と RQ
が垂直になるのは
a = [ナ]/[ニ], b =[ヌ]/[ネ]
のときであり, このとき PQ と RS
の内積は PQ・RS = [ノハヒ]/[フヘ]
となる。
第四問 (選択 20 点)
(1) 方程式 z3 = 2 + 2i ……………… ① を解こう。
複素数 2 + 2i を極形式で表すと
2 + 2i = [ア]√[イ](cos [ウエ]° + i sin[ウエ]°)
となる。
z = r(cos θ + i sin θ)
と置き, ① を満たす r, θ (r > 0. 0° ≦ θ < 360°)
を求めると,
r = [オ], θ =[カキ]°, [クケコ]°, 255°
となる。 従って, 複素数平面上の第二象限にある ① の解は
-[サ] + i である。
(2) 次に方程式 z6 - 4z3 + 8 = 0 ……………… ② の解について考えよう。 ② は (z3 - 2)2 = -[シ], 即ち z3 = 2± [ス]i となるから, (1) と同様に考えると, 第二象限にある ② の解は (1) で求めた -[サ] + i と ([セ] - √[ソ])/[タ] + (([チ] + √[ツ])/[テ])i の二個であり, 他の解は第一象限に一個, 第三象限に [ト] 個, 第四象限に [ナ] 個存在する。
出題者の注: この問題において複素数平面の象限とは, 実軸を x 軸, 虚軸を y 軸とした座標平面に於ける象限のことをいう。
第五問 (選択 20 点)
一枚の硬貨を三回投げ, 表が出た回数を X とする。 次に骰子を X 回振る。 (例えば X = 2 ならば, 骰子を二回振ることになる。) そうして, 1 又は 2 の目が出た回数を Y とする。 但し, X = 0 の場合は, Y = 0 と決める。
(1) X = 2 のとき, Y の取り得る値は [ア] 通りである。
(2) X = 2 となる確率は [イ]/[ウ] である。 X = 2 という条件のもとで, Y = 1 となる条件付確率は [エ]/[オ] である。 従って, X = 2, Y = 1 となる確率は [カ]/[キ] である。 同様にして X = 1, Y = 1 となる確率は 1/8 であり, X = 3, Y = 1 となる確率は 1/18 である。 従って, Y = 1 となる確率は [クケ]/[コサ] である。
(3) (2) と同様に計算すると Y = 2 となる確率は 5/72 であり Y = 3 となる確率は 1/216 である。 従って, Y = 0 となる確率は [シスセ]/[ソタチ] である。
(4) Y の平均 (期待値) は [ツ]/[テ] である。
(5) Y = 0 という条件のもとで, X = 2 となる条件付確率は [トナ]/[ニヌネ] である。
第六問 (選択 20 点)
正の整数 a1, a2, c が与えられたときに, s1
= a1 とし,
si = si-1 + ai (i
= 2, 3, ...) …… ①
ai+2 = ai+1 + ((si/c)
の整数部分) (i = 2, 3, ...) ……
②
によって得られる数の列, a3, a4, ..., an
を表示させる為に, 次のようなプログラムを作ってみた。
以下のプログラムにおいて INT(X) は X を超えない最大の整数を与える函数である。
100 INPUT "a1, a2, c ="; A, B, C
110 INPUT "n ="; N
120 S = A
130 FOR J = 3 TO N
140 A = B + INT(S/C)
150 PRINT "a("; J; ") = "; A
160 B = A
170 S = S + A
180 NEXT J
190 END
このプログラムが意図通りに動作するかどうか確かめてみる。
(1) このプログラムを実行し, a1, a2, c = ? に対して 1, 1, 1
を入力し, n = ? に対して 6 を入力すると
a(3) = [ア] a(4) = [イ] a(5) = [ウエ] a(6) = 34
が表示される。 又, a(6) が表示される直前の S の値は [オカ]
である。
(2) 次に, 定義の式 ①,
② に従って計算してみる。 a1 = 1, a2 = 1, c =
1 とすると
a3 = [キ], a4 = [ク], a5 = [ケ], a6 = [コサ], ...
となる。
(3) (1), (2) よりプログラムのどこかに誤りがあることが分かった。 このプログラムの 160 行, 170 行を修正して, 初めに意図したように動かしたい。
130 FOR J = 3 TO N 140 A = B + INT(S/C) 150 PRINT "a("; J; ") = "; A 160[シ]170[ス]180 NEXT J
の [シ], [ス] に当てはまるものを, 次の 0~9 の内から一つずつ選べ。
0. A = B 1. B = A 2. A = A + 1 3. B = B +
1 4. S = S + A
5. S = S + B 6. S = A 7. S = A + B 8. S = S + 1 9. S =
B + 1
(4) (3) のように修正したプログラムを実行し, a1, a2, c = ? に対して 1, 1, 2 を, n = ? に対して 6 を入力するとき, a(6) が表示される直前の B の値は [セ] である。
解答へ
センター試験の目次に戻る。