第一問 (必答 40 点)
[1] a を定数とし, 二次函数
y = -4x2 + 4(a - 1)x - a2
のグラフを C とする。
(1) C が点 (1, -4) を通るとき, a = [ ア ] である。
(2) C の頂点の座標は
( (a-1)/[ イ ], [ ウエ ]a + [ オ ]) である。
(3) a > 1 とする。 x が -1 ≦ x ≦ 1 の範囲にあるとき, この二次函数の最大値, 最小値を調べる。 最大値は
1 < a ≦ [ カ ] ならば -2a + [ キ ]
a > [ カ ] ならば -a2 + 4a - [ ク ] である。 又,
最小値は
-a2 - [ ケ ] a である。 最大値と最小値の差が 12 になるのは
a = -1 + [ コ ] √[ サ ] の時である。
[2] 二つの箱 A, B がある。
A の箱には, 次のように 6 枚のカードが入っている。
0 の数字が書かれたカードが 1 枚
1 の数字が書かれたカードが 2 枚
2 の数字が書かれたカードが 3 枚
B の箱には, 次のように 7 枚のカードが入っている。
0 の数字が書かれたカードが 4 枚
1 の数字が書かれたカードが 1 枚
2 の数字が書かれたカードが 2 枚
A の箱から 1 枚, B の箱から 2 枚, 合わせて 3 枚のカードを取り出す。
(1) 3 枚のカードに書かれた数が全て 0 である確率は [ シ ]/[ スセ ] である。
(2) 3 枚のカードに書かれた数の積が 4 である確率は [ ソ ]/[ タチ ] である。
(3) 3 枚のカードに書かれた数の積が 0 である確率は [ ツテ ]/[ トナ ] である。
(4) 3 枚のカードに書かれた数の積の期待値は [ ニヌ ]/[ ネノ ] である。
第二問 (必答 40 点)
[1] a, b を実数とし, x の整式 A, B を
A = x2 + ax + b, B = x2 + x + 1
とする。 但し, A と B は等しくないものとする。
(1) 等式
A2 + B2 = 2x4 + 6x3 + 3x2 + cx + d
が成り立つとき, a = [ ア ], b = -[ イ ], c = -[ ウ ], d = [ エ ] である。
(2) 等式
A2 - B2 = (A - B)(A + B)
= {(a - 1)x + (b - 1)}{[ オ ]x2 + (a + [ カ ])x + b + 1}
を考える。 A - B が x - 1 で割り切れるのは [ キ ] の時であり, 又, A + B が x - 1 で割り切れるのは [ ク ] の時である。 よって A - B と A + B が同時に x - 1 で割り切れることはない。 但し, [ キ ], [ ク ] については, 次の 1. -- 4. の中から当てはまるものをそれぞれ一つずつ選べ。
0. a + b = 0, 1. a - b = 0, 2. a + b - 2 = 0, 3. a + b + 4 = 0, 4. a - b - 2 = 0.
従って, A2 - B2 が (x - 1)2 で割り切れるのは, A + B が (x - 1)2 で割り切れる場合である。 このとき
a = -[ ケ ], b = [ コ ], A2 - B2 = [ サシス ] x(x - 1)2
となる。
[2] 半径 R の円に内接する四角形 ABCD が
AB = (√3) - 1, BC = (√3) + 1, cos ∠ABC = -1/4
を満たしており, △ACD の面積は △ABC の面積の 3 倍であるとする。
このとき,
AC = [ セ ], R = ([ ソ ]√[ タチ ])/[ ツ ] である。
又, △ACD と △ABC の面積についての条件から,
AD×CD = [ テ ], AD2 + CD2 = [ トナ ]
となる。 従って, 四角形 ABCD の長さは
[ ニ ]√[ ヌ ] + 2√3 である。
第三問 (選択 20 点)
(1) 初項が 0 でない等比数列 {an} が a1 + 2a2 = 0 を満たしている。 このとき, 公比は [ アイ ]/[ ウ ] である。 a1 + a2 + a3 = 9/4 ならば, a4 + a5 + a6 = [ エオ ]/[ カキ ] であり, 1/a1 + 1/a2 + … + 1/an = 57 となるのは n = [ ク ] の時である。
(2) bn = pn + q で表される数列 {bn} に大して, 初項から第 n 項までの和を Sn とする。 b7 = 1, S12 = 10 ならば, p = [ ケ ]/[ コ ], q = [ サシ ]/[ ス ] であり, S1 + S1 + … + S12 = [ セソ ]/[ タ ] である。
第四問 (選択 20 点)
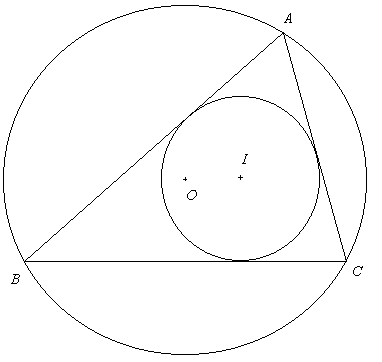
三角形 ABC の外心を O, 内心を I, 又, 外接円の半径を R, 内接円の半径を r とする。 O と I が一致しない場合に R, r と OI の関係を調べよう。 ア -- サ は A -- G の中からC 以外の当てはまる文字を選べ。 但し, エ と オ は解答の順序を問わない。
AI の延長と外接円の交点を D とし, DO の延長と外接円の交点を E とする。 又直線 OI と外接円の交点を F, G とし F, O, I, G がこの順に並ぶものとする。 I から AC へ垂線を引き, 交点を H とする。

△AHI と △EBD は ∠HAI = ∠[ アイ ]I = ∠BED, ∠AHI = ∠EBD = 90゜ であるから相似で, ED : [ ウ ]I = [ エオ ] : HI が成り立ち
[ ウ ]I・[ エオ ] = 2rR ……………… (1)
次に △DBI に於いて
∠DIB = ∠I[ カキ ] + ∠IBA, ∠DBI + ∠IBC
∠IBA = ∠IBC, ∠I[ カキ ] = ∠DAC = ∠DBC
であるから, ∠DIB = ∠[ クケ ]I で, △DBI
は二等辺三角形となり
[ エオ ] = ID ……………… (2)
△IFD と △IAG に於て ∠IFD = ∠GFD = ∠IAG, ∠FID = ∠AIG. 従って △IFD と △IAG は相似であり
AI・[ コ ]I = [ サ ]I・GI
= ([ サ ]O + OI)(GO - OI)
= R2 - OI2.
(1), (2), (3) から OI2 = R2 - [ シ ] が成り立つ。 但し, [ シ ] には次の 0 -- 5 の中から正しいものを一つ選べ。
0. r, 1. R, 2. r2, 3. rR, 4. 2rR, 5. 4rR.
第五問 (選択 20 点)
次のプログラムは x = 0, 1, ......, 9 に対する ax2 + bx + c の値の最小値と最大値を求めるものである。 [ アイウ], [ エオカ ] に適当な行番号を入れてプログラムを完成させよ。
100 INPUT "a = "; A
110 INPUT "b = "; B
120 INPUT "c = "; C
130 U = C
140 V = C
150 FOR X = 0 TO 9
160 Y = A*X*X + B*X + C
170 IF Y >= U THEN GOTO [ アイウ]
180 U = Y
190 IF Y <= V THEN GOTO [ エオカ ]
200 V = Y
210 NEXT X
220 PRINT "最小値 = "; U
230 PRINT "最大値 = "; V
240 END(1) 上のプログラムを実行して, a = ? に対して -1, b = ? に対して 7, c = ? に対して 28 を入力すると, 180 行は [ キ ] 回, 200 行は [ ク ] 回実行され
最小値 = [ ケコ ] 最大値 = [ サシ ]
が表示される。 又, 170 行の不等号 >= を > に, 190 行の不等号 <= を < に変更した後, 同じデータを入力すると, 180 行は [ ス ] 回, 200 行は [ セ ] 回実行され
最小値 = [ ソタ ] 最大値 = [ チツ ]
が表示される。
(2) 冒頭のプログラムの 170 行と 180 行は, 180 行を削除して 170 [ テ ] と書き直しても同じ結果を得る。 同様に 190 行と 200 行でも 200 行を削除して, 190 行を 190 [ ト ] と書き直すことが出来る。 但し, [ テ ] と [ ト ] については, 次の 0 -- 5 の中から最も相応しいものを一つずつ選べ。
0. IF Y > U THEN U = Y
1. IF Y < U THEN U = Y
2. IF Y = U THEN U = Y
3. IF Y > V THEN V = Y
4. IF Y < V THEN V = Y
5. IF Y = V THEN V = Y
解答へ。
センター試験の目次に戻る。