2005 年数学 I ・ A 問題

Sunday, 16th January, 2005.
11:35 -- 12:35(1hr)
平均 69.43

第一問, 第二問は必答。
第三問から第五問までのうちから一問選択。
計三問を解答。

第一問 (必答 40 点)

[1] a を定数とし, x の二次函数

y = x² - 2(a + 2)x + a² - a + 1

のグラフを G とする。

(1) グラフ G と y 軸との交点の y 座標を Y とする。 Y の値が最小になるのは a = [ ア ]/[ イ ] の時で, 最小値は [ ウ ]/[ エ ] である。この時グラフ G は x 軸と異なる二点で交わり, その交点の x 座標は
([ オ ] ±√[ カキ ])/[ ク ] である。

(2) グラフ G が y 軸に関して対称になるのは a = -[ ケ ] の時で, この時のグラフを G₁ とする。
グラフ G₁ が x 軸に接するのは a = -[ コ ]/[ サ ] の時で, この時のグラフを G₂ とする。
グラフ G₁ を x 軸方向に [ シ ]/[ ス ], y 軸方向に [ セソ ] だけ平行移動するとグラフ G₂ に重なる。

[2] 大小二個の骰子を投げ, 出た目の数をそれぞれ a, b とし, 二次函数
y = x² - (b - 2)/a のグラフを C とする。

(1) グラフ C と x 軸との共有点の個数が 0 個である確率 (即ちグラフ C が x 軸と共有点を持たない確率) は [ タ ]/[ チ ] であり, 共有点の個数が一個である確率は [ ツ ]/[ テ ], 共有点の個数が二個である確率は [ ト ]/[ ナ ] である。

(2) グラフ C と x 軸との共有点の期待値は [ ニ ]/[ ヌ ] である。

(3) グラフ C と x 軸が共有点を持ち, 且つ共有点の x 座標が全て整数となる確率は [ ネノ ]/[ ハヒ ] である。

第二問 (必答 40 点)

[1] a, b を実数とし, x の整式
A = ⁴ + (a² - a - 1)x² + (-a² + b)x + b³,
B = x² - x - a
を考える。 A を B で割った章を Q, 余りを R とすると,
Q = x² + x + a^{[ ア]}
R = (a + b)x + a^{[ イ ]} + b^{[ ウ ]}
である。

(1) R = x + 7 の時, a = ［エ ] 又は a = [ オカ ] である。

(2) [ キ ] と [ ク ] に当てはまるものを, 次の 0 から 3 のうちから一つずつ選べ。
(i) a < -1/2 は, 全ての実数 x に対して Q > 0 となるための [ キ ] 。
(ii) a + b = 0 は, A が B で割り切れるための [ ク ]。

0 必要十分条件である。
1 必要条件であるが十分条件ではない。
2 十分条件であるが必要条件ではない。
3 必要条件でも十分条件でもない。

[2] 線分 AB を直径とする半円周上に二点 C, D があり,
AC = 2√5, AD = 8, tan∠CAD = 1/2 であるとする。

この時, cos∠CAD = ([ ケ ]√[ コ ])/[ サ ]
CD = [ シ ]√[ ス ] である。

更に, △ADC の面積は [ セ ],
AB = [ ソタ ] である。

第三問 (選択 20 点)

(1) 数列 {a_n} の初項から第 n 項までの和 S_n = Σ_k=1ⁿ a_k が
S_n = -n² + 24n (n = 1, 2, 3, ......)
で与えられるものとする。この時 a₁ = [ アイ ], a₂ = [ ウエ ] である。又 a_n < 0 となる自然数 n の値の範囲は n ≧ [ オカ ] であり,
Σ_k=1⁴⁰|a_k| = [ キクケ ] となる。

(2) 初項 1, 公比 3 の等比数列を {b_n} と置く。各自然数 n に対して, b_k ≦ n を満たす最大の b_k を c_n と置く。例えば, n = 5 の時
b₂ = 3, b₃ = 9 であり, b₁ < b₂ ≦ 5 < b₃ < b₄ < …
なので c₅ = b₂ = 3 である。

(i) c₁₁ = [ コ ] であり, c_n = 27 である自然数 n は全部で [ サシ ] 個ある。
(ii) Σ_k=1³⁰ c_k = [ スセソ ] である。

第四問 (選択 20 点)

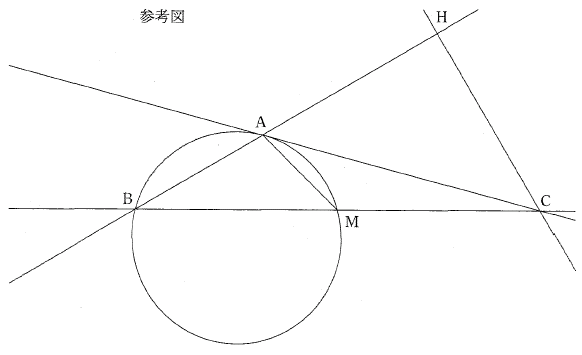
△ABC に於いて, ∠A は鈍角で, ∠B = 30°である。点 C から直線 AB に引いた垂線と直線 AB との交点を H とする。辺 BC の中点を M とし, 直線 AC は三点 A, B, M を通る円と点 A で接しているとする。

下の [ ア ] から [ ウ ], [ オ ], [ ク ] に付いては, 最も適当なものを次の 0 から F の内から一つずつ選べ。

0 鋭角三角形 1 直角二等辺三角形 2 二等辺三角形
3 正三角形 4 直角三角形

5 ABC 6 AMB 7 HMC
8 MAB 9 MCA

A AB B AC C AM
D BC E BH F CH

直角三角形 HBC に於て ∠HBC = 30°なので, BC = 2[ ア ] である。一方 ∠MAC = ∠[ イ ] なので, △MAC と △[ イ ] は相似になる。従って
AC² = MC・[ ウ ]
となる。 M は辺 BC の中点なので
AC = (√[ エ ])CH
が成り立つ。従って △HAC は [ オ ] であり, ∠AMB = [ カキ ]°となる。

AC と HM の交点を K, 直線 BK と HC の交点を L とする。 △HBK と △BCK の面積比は HL : LC であり, △CHK と △BCK の面積比は
△CHK : △BCK = HA : [ ク ]
である。又, M は辺 BC の中点だから, △HBK と△CHK の面積は等しい。故に, HL : LC = HA : [ ク ] が成り立つ。

従って △HAL と △HBC の面積比は
△HAL : △HBC = 1 : [ ケ ] となる。

第五問 (選択 20 点)

次のプログラムを考える。但し, N には自然数を入力するものとする。又, INT(X) は X を超えない最大整数を与える函数である。

100 INPUT "N = "; N
110 IF N > 9 THEN GOTO 230
120 FOR A = 1 TO N
130   FOR B = 1 TO N
140     IF B = 2*INT(B/2) THEN GOTO 210
150     IF B = A THEN GOTO 210
160       FOR C = 1 TO N
170       IF C = A THEN GOTO 200
180       IF C = B THEN GOTO 200
190       PRINT 100*A + 10*B + C
200     NEXT C
210   NEXT B
220 NEXT A
230 END

(1) 上のプログラムを実行し N = ? に 3 を入力すると, 三桁の数が [ ア ] 個表示される。特に, 二番目に表示される三桁の数は [ イウエ ] である。

(2) 上のプログラムを実行し, N = ? に 5 を入力すると 150 行は [ オカ ] 回実行され, [ イウエ ] は [ キ ] 番目に表示される。

(3) 上のプログラムの 160 行と 180 行を, それぞれ次のように書き直す。

160 FOR C = B TO N

180 IF C = B*INT(C/B) THEN GOTO 200

変更したこのプログラムを実行し, N = ? に 7 を入力する。この時, 表示される三桁の数のうち, 最大の数は [ クケコ ] であり, 300 以上 500 以下の数は [ サ ] 個である。

解答へ。

センター試験の目次に戻る。

2005 年 数学 I ・ A 問題

2005 年数学 I ・ A 問題