第一問 (20 点)
[1] α = ((√7) - √3)2/(7 - 3) = (10 - 2√21)/4 = (5 - √21)/2. (3 点)
6x2 - 7x = 0
(5x - 1)(x - 1) = 0
x = 1/6, 1. (両方で 2 点)
(式 0) = (5 - √21)/2,
(式 1) = (5 + √21)/2,
(式 2) = 1/6,
(式 3) = 1.
明らかに (式 0) < (式 1), (式 2) < (式 3) であるから, 問題なのは (式 0) と (式 2) の大小関係である。
ここで (式 0) - (式 2) = (5 - √21)/2 - 1/6 = (14 - 3√21)/6 = ((√196) - √189)/6 > 0.
となるので, (式 0) > (式 2) である。 従って 2. (3 点)
[ ク ] が少し迷うかもしれないが, そんなに難しくない。
[2]
先ず p: ∃m: n = 5m + 1.
q: ∃k: n = 10k + 1.
r: ∃N: n = 2N + 1.
s: n は奇素数
である。
「p 且つ q」 ということは n = 5m + 1 = 2N + 1 ということを意味しており, 従って, 5m = 2N でなければならない。 この時 m は偶数でなければならないから, m = 2M と書け, 従って, n = 5・2M + 1 = 10M + 1.
従って q が成り立つから, 先ず十分条件ではある。
次に, q であれば, n = 10k + 1 = 5・(2k) + 1 = 2・(5k) + 1 であるから 「p 且つ q」 が成り立ち, 従って必要条件でもある。
以上より必要十分条件であるから 0. (3 点)
`r は ∃N: n = 2N を意味しており,
`s は n が奇素数でないことを意味している。
すると`r ならば`s (即ち, 偶数ならば奇素数でない) は真である。
又`s ならば`r (即ち, 奇素数でなければ偶数) は正しくない。 反例は n = 9.
従って 2. (3 点)
p 且つ s は n = 5m + 1 が奇素数 を意味している。
q 且つ s は n = 10k + 1 が奇素数 を意味している。
素数ということを除いて考えれば, n = 5m + 1 が奇数ならば 5m が偶数なので, m が偶数。 従って n = 10k + 1 と書けることになる。 逆は明らかであるから, 0. (3 点)
R⊃S は明らかなので 4 と 7 はおかしい。
例えば 11 = 5・2 + 1 は奇素数なので 6 はおかしい。
5 はすべての条件を満たしているので 5.(3 点).
そんなに難しくない。
落ち着いてやれば大丈夫。
第二問 (25 点)
G2: y = (x + a)2 + b - a2 … (3)
の頂点は, (-a, b - a2) で, これが G1 の上にあるので
b - a2 = 3a2 + 2a - 1.
b = 4a2 + 2a - 1. (3 点)
よって, G1 の頂点は (-a, 3a2 + 2a - 1). (2 点)
(1) G2 の頂点の y 座標は
3a2 + 2a - 1
= 3(a2 + (2/3)a) - 1
= 3((a + 1/3)2 - 1/9) - 1
= 3(a + 1/3)2 - 4/3.
より a = -1/3 (3 点) の時最小値 -4/3 (3 点) を採る。
a = -1/3 を (3) に代入すると
y = (X - 1/3)2 - 4/3 なので,
軸は x = 1/3 (2 点), で, G2 の x 軸との交点の x 座標は
x - 1/3 = ±2/√3 = ±2(√3)/3.
よって x = (1 ± 2√3)/3. (4 点)
(2) (0, 5) を通るので, b = 5 即ち,
5 = 4a2 + 2a - 1.
4a2 + 2a - 6 = 0
2a2 + a - 3 = 0
(2a + 3)(a - 1) = 0
故に a = 1, -3/2. (各 2 点)
ここで a = 1 とすると頂点は (-1, 4) だが, これを x 軸方向に k, y 軸方向に k 平行移動すると (-1 + k, 4 + k) になる。
これが G1 上にあるので
4 + k = 3(k - 1)2 - 2(k - 1) - 1
3k2 - 9k = 0.
3k(k - 3) = 0.
即ち k = 0, 3.
k ≠ 0 より k = 3. (4 点)
誘導の通りやれば良いので難しくない。
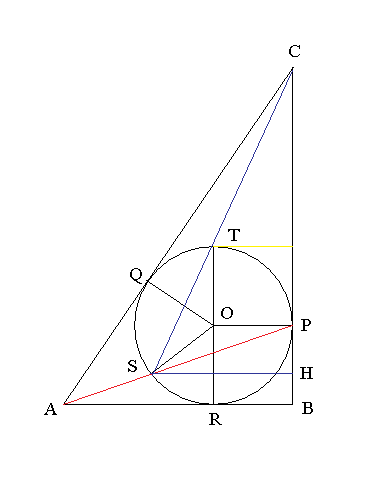
第三問 (30 点) 図を描きながらやること。

(1) OP = OR = r とすると, 面積を考えて
(1/2)・(3 + 4 + 5)r = (1/2)・3・4
よって r = 1. (3 点)
cos A = 3/5, AQ = AR = AB - OP = 2 なので (第二) 余弦定理より
QR2
= 22 + 22 - 2・2・2cosA
= 8 - 24/5 = 16/5.
QR > 0 より QR = 4(√5)/5. (3 点)
正弦定理より
QR/sin∠QPR = PR/sin∠PQR
sin∠QPR
= QR(sin∠PQR)/PR
= (4(√5)/5)sin45°/√2
= (4(√5)/5)/2 = 2(√5)/5. (3 点)
(2) AP = √(32 + 12) = √10. (3 点).
OP || AB だから ∠OPA = ∠PAB で, OP = OS だから
SP = 2OPcos∠OPA
= 6/√10 = 3(√10)/5. (3 点)
△ABP ∽ △ SHP より HP = 3/5. (2 点)
同様に SH = 9/5. (2 点)
tan∠BCS = SH/HC= (9/5)/(4 - 2/5) = 9/18 = 1/2. (3 点).
(3) (T から BC に垂線を降ろして考えると直ぐに分かるように) tan∠BCT = 1/2. (2 点)
よって, C, T, S は同一直線上にある。
△TRS は TR が直径で, S が同一円周上にあるので, ∠RSC = ∠RST = 90°(3 点)
従って円周角定理より ∠PSC = (1/2)∠POT = 45°. (3 点)
図を描きながらやらないと難しい。
SP の長さを出すのも気付かないと難しい。
第四問 (25 点)
全部で玉が 11 個あるので,
11C5 = (11・10・9・8・7)/(5・4・3・2・1) = 2・3・7・11 = 462 [通り] (4 点)
(1) 黒玉が含まれていて 0 点の場合
赤玉のみ 4 個ならば 5C4 = 5.
赤玉 3 個, 白玉 1 個ならば, 白玉の選び方が 5 通りで, その各々について, 白とは違う数を三つ選ぶのだから 5・4C3 = 20.
赤玉白玉各々二個ならば先ず先ず赤を二つ選んで置いて, それとは違う番号の白を選べば良いから 5C2・5 - 2C2 = 30.
赤 1, 白 3 だと上と同様で 20.
白のみ四個の場合も上と同様で 5.
以上より 5 + 20 + 30 + 20 + 5 = 80 [通り] (3 点)
黒玉が含まれていないで 0 点の場合。
赤のみは 1 通り。
赤4, 白 1 は白の数の選び方だけなので 5 通り
赤 3, 白 2 の場合は同様に 5C2 = 10.
赤 2, 白 3 も同様に 10.
赤 1, 白 4 は 5,
白のみ 1 の場合も 1 通り。
1 + 1 + 1 + 3
以上より 1 + 5 + 10 + 10 + 5 + 1 = 32 [通り]. (3 点)
黒玉が含まれていて 1 点の場合。
どの番号で一致するかということで 5 通りずつある。 その各々について考える。
赤 1, 白 3 の場合は残りの白 2 は他の数なら何でもいいので 4C2 = 6 [通り].
赤 2, 白 2 の場合は残りの赤白一つずつ違う番号にするので 4P2 = 12 [通り].
赤 3, 白 1 は上記と同様に 6 通り。
以上から 5・(6 + 12 + 6) = 120 [通り]. (3 点)
黒玉が含まれていないで 1 点の場合。
どの番号で一致するかということで 5 通りずつというのは上記と同じ。 その各々について考える。
赤 1, 白 4 ならば 4C3 = 4 [通り].
赤 2, 白 3 ならば (赤のもう一個の選び方)・(白 2 個の番号を更に残りから選ぶ) = 4・3C2 = 12 [通り].
赤 3, 白 2 は同様で 12 通り。
赤 4, 白 1 も上記と同様で 4 通り。
以上より 5・(4 + 12 + 12 + 4) = 160 [通り] (3 点)
(2) (1) から 1 点の場合は
(120 + 160)/(2・3・7・11) = 20/33. (3 点)
0 点の場合は (80 + 32)/(2・3・7・11) = 8/33.
よって 2 点の場合は 1 - 20/33 - 8/33 = 5/33. (3 点)
従って期待値は 1・20/33 + 2・5/33 = 30/33 = 10/11. (3 点)
場合分けの数が少ないので落ち着いてやれば間違いなく出来ると思われる。
今年の数学 I ・ A も難しくはないが, 間違え易くケアレスミスが致命的だったのではないか。
センター試験の目次に戻る。