2014 年 数学 I ・ A 解答と解説

第一問 (20 点)

[1] (1) a = ((√3) + 1)/((√2) + １), b = ((√3) - 1)/((√2) - １) である。

ab = (3 - 1)/(2 - 1) = 2. (1 点)

a + b = (((√3) + 1)((√2) - １) +  ((√3) - 1)((√2) + １))/(((√2) + １)((√2) - １))
= (√6) - (√3) + (√2) - 1 + (√6) - (√2) + (√3) - 1
= 2(- 1 + √6). (2 点)

a² + b²
= (a + b)² - 2ab
= 4(7 - 2√6) - 4 = 4(6 - 2√6) = 8(3 - √6). (2 点)

(2) a² + b² + 4(a + b) = 8(3 - √6) + 8(-1 + √6) = 8・2 = 16. (2 点)

従ってこの両辺に a² を掛けて
a²(a² + b² + 4(a + b)) = 16a²
a⁴ + a²b² + 4a³ + 4a²b = 16a²
a⁴ + (ab)² + 4a³ + 4ab・a = 16a²
a⁴ + 4 + 4a³ + 8a = 16a²
a⁴ + 4a³ - 16a² + 8a + 4 = 0. (3 点)

最初の一行は不要のようではあるが, このようにしておくと後の計算間違いを少なく出来る。
分母の有理化はしない方が良い。

(2) の後半だが, 問題としては簡単なのだが意外に思いつかない。

[2] 先ず 5 < √n < 6 ⇔ 25 < n < 36 である。

(1) n(U) = 35 - 25 = 10. (2 点)

以下では否定の記号として`p の代わりに ¬p と書くことにする。

(2) P∩R は 12 の倍数の集合で, 24, 36 の間にはないから空集合。
P∩S は 28 の倍数の集合であって, 28 自身を要素として持つ。
Q∩R は 30 の倍数の集合であって同様。
P∩`Q は4 の倍数であって 5 の倍数ではないものの集合であるので, 例えば 4・7 = 28 等を要素として持つ。
R∩`Q は6 の倍数であって 5 の倍数ではないものの集合であるが, 6・.4 = 24, 6・6 = 36 となるから, 空集合となる。
従って, 0, 4 (4 点)

(3) P∪R は 4 の倍数であるか 6 の倍数であるものの集合であることを意味しているから, それが全て 5 の倍数であるかどうかが問題である。 つまり 4 の倍数又は 6 の倍数ならば 5 の倍数ではないということを主張しているが, 6・5 = 30 が反例となっているので, 正しくない。

S∩`Q は7 の倍数で且つ 「5 の倍数でない」 ものだから, それがすべて 4 の倍数であるかということが問題だが, (7・3 =21 で) 7・4 = 28 (, 7・6 = 42) なので正しい。

 `Q∩`S ⊂`P ⇔ P ⊂ Q∪S であるが, つまり 4 の倍数は 5 又は 7 の倍数かということである。 この場合 4・8 = 32 があるので正しくない。

`P∩`Q⊂`S ⇔ S ⊂ P∩Q つまり, 7 の倍数は 20 の倍数であるかということだがそういう数はこの範囲にはないので正しくない。

`R∩`S ⊂`Q ⇔ Q ⊂ R∪S つまり, 5 の倍数は 6 又は 7 の倍数であるかということだが, (5.・5 = 25,) 5・6 = 30, 5・7 = 35, (5・8 = 40) だから正しい。

以上より 1, 4. (4 点)

(3) が少しややこしくて難しいか。
落ち着いてやれば難しくはない。

第二問 (25 点)

G: y = (x + a)² + 2a² - 6a - 36 なので頂点は
(-a, 2a² - 6a - 36), である。 (3 点)

(1) G と y 軸との交点は x = 0 の時だから
p = 3a² - 6a - 36.

ここで p = -27 とすると
3a² - 6a - 36 = -27
a² - 2a - 12 = -9
a² - 2a - 3 = 0
(a + 1)(a - 3) = 0.
だから a = 3, -1. (2 点)

a = 3 の時の頂点は (-3, 2・9 - 6・3 - 36) = (-3, 18 - 18 - 36) = (-3, -36).
a = -1 の時の頂点は (1, 2 + 6 - 36) = (1, 8 - 36) = (1, -28)
なので x 軸方向に 1 - (-3) = 4 (2 点), y 軸方向に -28 - (-36) = 8 (2 点) 平行移動すると一致する。

(2) G が x 軸と共有点を持つ
⇔ 2a² - 6a - 36 ≦ 0.
a² - 3a - 18 ≦ 0
(a + 3)(a - 6) ≦ 0
故に -3 ≦ a ≦ 6. (左辺が 1 点, 不等号が一組で 1 点, 右辺が 1 点, 不等号は共に 3 にマーク)

p = 3a² - 6a - 36
= 3(a² - 2a) - 36
= 3(a - 1)² - 39.
又, 軸と端点との距離を調べると |1 - 3| = 2, |6 - 1| = 5 なので

a = 1 (3 点) で最小値 -39 (1 点), a = 6 (3 点) で最大値 36 (1 点).

全ての共有点の x 座標が - 1 よりも大きくなるということなので
x = -1 の時の
y = 1 - 2a + 3a² - 6a - 36
= 3a² - 8a - 35
= (3a + 7)(a - 5) > 0
即ち a < -7/3, 5 < a.

更に軸を考えると
x = -a > -1
即ち a < 1.

これらと元々の a の範囲 -3 ≦ a ≦ 6 とから
-3 ≦ a < -7/3. (左辺と右辺は各 2 点, 不等号は左側が 3, 右側が 1 で両方出来て 1 点)

(2) の後半がやや難しいか。
その他は基本。

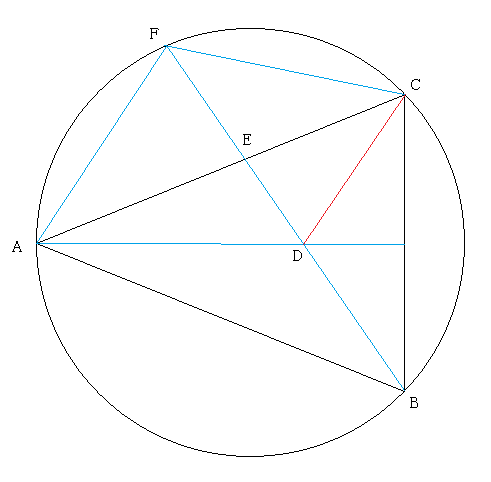
第三問 (30 点) 図を描きながらやること。

(第二) 余弦定理より
CA² = 4² + 2² - 2・4・2・(1/4) = 16 + 4 - 4 = 16.
CA > 0 より CA = 4. (3 点)

再び (第二) 余弦定理より
BC² = AB² + AC² - 2AB・ACcos∠BAC
4 = 16 + 16 - 2・16cos∠BAC
1 = 4 + 4 - 2・4cos∠BAC
8cos∠BAC = 7
故に cos∠BAC = 7/8. (3 点).

0°< ∠BAC < 180°より
sin∠BAC = √(1 - cos²∠BAC)
= √(1 - (7/8)²) = (√(8² - 7²))/8
= (√15)/8. (3 点).

正弦定理より
2R = BC/sin∠BAC = 2/((√15)/8)
= 16/√15 = (16√15)/15.
R = (8√15)/15. (3 点)

(1) AE : EC = AB : BC = 2:1 なので
AE = 4・(2/3) = 8/3. (4 点)

(2) △ABE で (第二) 余弦定理より
BE² = AB² + AE² - 2AB・AEcos∠BAC
= 16 + 64/9 - 2・4・(8/3)・(7/8)
= 16 + 64/9 - 56/3)
= 8・(2 + 8/9 - 7/3)
= 8・(18 + 8 - 21)/9
= 8・5/9 = 40/9.
BE > 0 より BE = 2(√10)/3. (4 点)

BD : DE = AB : AE = 4 : (8/3) = 1 : (2/3) = 3 : 2 なので
BD = BE・3/5 = (2√10)/5. (4 点)

△EBC ∽ △EAF で, 相似比は
EB : EA = ((2√10)/3) : (8/3) = (√10) : 4.
故に
△EBC/△EAF = ((√10)/4)² = 10/16 = 5/8. (3 点)

(3) △FAC で FA の対角は ∠FCA = ∠FBA = ∠B/2.
同様に FC の対角は ∠FAC = ∠FBC = ∠B/2.
従って FA = FC.

そして △FDC で
∠FCD = ∠FCA + ∠ACD
= ∠FBA + ∠C/2 = ∠B/2 + ∠C/2 = ∠B.
同様に
∠FDC = ∠DCB + ∠DBC ∠B/2 + ∠C/2 = ∠B.
なので  ∠FCD = ∠FDC. つまり FC = FD.

以上より 4 (3 点)

図を描きながらやらないと難しい。
(2) の相似は最初気付かずに苦労した。
又 (3) で △FDC が二等辺三角形であることの証明 (△DAF でも良いが) が思い付かず苦労した。

第四問 (25 点)

(1) 二回ずつということだから 4!/(2!2!) = 4・3/2 = 6 (2 点)

(2) 3, 4, 5 の方向に一回ずつだから 3! = 3・2・1 = 6 通り (2 点)

(3) C→D は (2) 同様に 6 通りだから, A→C は 36 通り。 (3 点)
で, 確率は 6²/6⁶ = 1/6⁴ = 1/1296. (3 点)

(4) 4 が 5 個, 1 が 1 個であるから 6 通り。 (3 点)

2 が一つ, 5 が一つ, 残りは 4 だから ₆P₂ = 6・5 = 30 通り。 (3 点)

6 の→を含む時は 2 を含む場合と同じ。

それ以外は 4 は 2 回 (3 点) と決まるので
6!/(2!2!2!) = (6・5・4・3)/(2・2) = 90 通り。 (3 点)

よって全て足すと
6 + 30・2 + 90 = 156 通り。 (3 点)

最後の合計の時に 「同じ」 とした所を足すのを忘れないように。

今年の数学 I ・ A は簡単だった去年よりも更に簡単になったと言われている。
難しそうな二三問で差がついたかもしれない。
ケアレスミスが致命的だったのではないかと思われる。

センター試験の目次に戻る。