2014 年数学 II ・ B 問題

Sunday, 19th January, 2014.
14:50 -- 15:50 (1hr)
平均 53.94

注: この科目には, 選択問題があります。

第一問, 第二問は必答。
第三問から第六問のうちから二問選択。
計四問を解答。

第一問 (必答 30 点)

[1] O を原点とする座標平面上に於いて, 点 P(p, q) を中心とする円 C が, 方程式 y = (4/3)x で表される直線 l に接しているとする。

(1) 円 C の半径 r を求めよう。
点 P を通り直線 l に垂直な直線の方程式は

y =  -([ ア ]/[ イ ])(x - p) + q

なので, P から l に引いた垂線と l の交点 Q の座標は

((3/25)([ ウ ]p + [ エ ]q), (4/25)([ ウ ]p + [ エ ]q))

となる。

求める C の半径 r は, P と l の距離 PQ に等しいので

r = (1/5)|[ オ ]p - [ カ ]q| ………………………… �@

である。

(2) 円 C が, x 軸に接し, 点 R(2, 2) を通る場合を考える。 この時, p > 0, q > 0 である。 C の方程式を求めよ。

C は x 軸に接するので, C の半径 r は q に等しい。 従って, �@ により, p = [ キ ]q である。

C は点 R を通るので, 求める C の方程式は

(x - [ ク ]) + (y - [ ケ ])² = [ コ ] ………………………… �A

又は

(x - [ サ ]) + (y - [ シ ])² = [ ス ] ………………………… �A

である事が分かる。 但し [ コ ] < [ ス ] とする。

(3) 方程式 �A の表す円の中心を S, 方程式 �B の表す円の中心を T と置くと, 直線 ST は原点 O を通り, 点 O は線分 ST を [ セ ] する。 [ セ ] に当てはまるものを次の 1 から 5 の内から一つ選べ。

0 1 : 1 に内分
1 1 : 2 に内分
2 2 : 1 に内分
3 1 : 1 に外分
4 1 : 2 に外分
5 2 : 1 に外分

[2] 自然数 m, n に対して, 不等式

log₂m³ + log₃n² ≦ 3 ………………………… �C

を考える。

m = 2, n =１ の時 log₂m³ + log₃n² = [ ソ ] であり, この m, n の値の組は �C を満たす。

m = 4, n = 3 の時 log₂m³ + log₃n² = [ タ ] であり, この m, n の値の組は �C を満たさない。

不等式 �C を満たす自然数 m, n の個数を調べよう。 �C は

log₂m + ([ チ ]/[ ツ ])log₃n ≦ [ テ ] ………………………… �D

と変形出来る。

n が自然数の時,  log₃n の採り得る最小の値は [ ト ] であるから, �D により, log₂m ≦ [ テ ] でなければならない。 log₂m ≦ [ テ ] により, m = [ ナ ] 又は m = [ ニ ] でなければならない。 但し [ ナ ] < [ ニ ] とする。

m = [ ナ ] の場合, �D は, log₃n ≦ [ ヌ ]/[ ネ ] となり, n² ≦ [ ノハ ] と変形出来る。 よって m = [ ナ ] の時, �D を満たす自然数 n の採り得る値の範囲は n ≦ [ ヒ ] である。 従って m = [ ナ ] の場合, �C を満たす自然数 m, n の組の個数は [ ヒ ] である。

同様にして, m = [ ニ ] の場合, �C を満たす自然数 m,. n の組の個数は [ フ ] である。

以上の事から, �C を満たす自然数 m, n の組の個数は [ ヘ ] である。

第二問 (必答 30 点)

p を実数とし, f(x) = x³ - px とする。

(1) 函数 f(x) が極値を持つ為の p の条件を求めよう。 f(x) の導函数は, f '(x) = [ ア ]x^{[ イ ]} - p である。 従って, f(x) が x = a で極値をとるならば [ ア ]a^{[ イ ]} - p = [ ウ ] が成り立つ。 更に, x = a の前後での f '(x) の符号の変化を考えることにより, p が条件 [ エ ] を満たす場合は, f(x) は必ず極値を持つことが分かる。 [ エ ] に当てはまるものを, 次の 1 から 4 の内から一つ選べ。

0 p = 0
1 p > 0
2 p ≧ 0
3 p < 0
4 p ≦ 0

(2) 函数 f(x) が x = p/3 で極値をとるとする。 又, 曲線 y = f(x) を C とし, C 上の点 (p/3, f(p/3)) を A とする。

F(x) が x = p/3 で極値をとることから, p = [ オ ] であり, f(x) は x = [ カキ ] で極大値をとり, x = [ ク ] で極小値をとる。

曲線 C の接線で, 点 A を通り傾きが 0 でないものを l とする。 l の方程式を求めよう。 l と C の接線の x 座標を b とすると, l は点 (b, f(b)) に於ける C の接線であるから, l の方程式は b を用いて

y = ([ ケ ]b² - [ コ ])(x - b) + f(b)

と表すことが出来る。 又, l は点 A を通るから, 方程式

[ サ ]b³ - [ シ ]b² + 1 = 0

を得る。 この方程式を解くと b = [ ス ], [ セソ ]/[ タ ] であるが, l の傾きが 0 でないことから, l の方程式は

y = ([ チツ ]/[ テ ])x + [ ト ]/[ ナ ]

である。

点 A を頂点とし, 原点を通る放物線を D とする。 l と D で囲まれた図形の内, 不等式 x ≧ 0 の表す領域に含まれる部分の面積 S を求めよう。 D の方程式は

y = [ ニ ]x² - [ ヌ ]x

であるから, 定積分を計算することにより, S = [ ネノ ]/24 となる。

第三問--第六問は, 何れか二問を選択し, 解答しなさい。

第三問 (選択 20 点)

数列 {a_n} の初項は 6 であり,  {a_n} の階差数列は初項が 9, 公差が 4 の等差数列である。

(1) a₂ = [ アイ ], a₃ = [ ウエ ] である。 数列 {a_n} の一般項を求めよう。 {a_n} の階差数列の第 n 項が  [ オ ] + [ カ ] であるから, 数列 {a_n} の一般項は

a_n = [ キ ]n^{[ ク ]} + [ ケ ]n + [ コ ] ………………………… �@

である。

(2) 数列 {b_n} は初項が 2/5 で, 漸化式

b_{n + 1} = (a_n/(a_{n + 1} - 1))b_n  (n  = 1, 2, 3, ...) ………………………… �A

 を満たすとする。 b₂ = [ サ ]/[ シス ] である。 数列 {b_n} の一般項と初項から第 n 項までの和 S_n を求めよう。

�@, �A により, 全ての自然数 n に対して

b_{n + 1} = (([ セ ]n + [ ソ ])/([ セ ]n +  [ タ ]))b_n ………………………… �B

が成り立つことが分かる。

ここで

c_n = ([ セ ]n + [ ソ ])b_n ………………………… �C

とする時, �B を c_n と c_{n + 1} を用いて変形すると, 全ての自然数 n に対して

([ セ ]n + [ チ ])c_{n + 1} = ([ セ ]n + [ ツ ])c_n

が成り立つことが分かる。 これにより

d_n = ([ セ ]n + [ テ ])c_n ………………………… �D

と置くと, 全ての自然数 n に対して d_{n + 1} = d_n が成り立つことが分かる。 d₁ = [ ト ] であるから, 全ての自然数 n に対して, d_n = [ ト ] である。

従って, �C と �D により, 数列 {b_n} の一般項は

b_n = [ ト ]/(([ セ ]n + [ ソ ])([ セ ]n + [ テ ]))

である。 又

b_n = [ ナ ]/([ セ ]n + [ ソ ]) - ［ ニ ]/([ セ ]n + [ テ ]))

が成り立つことを利用すると, 数列 {b_n} の初項から第 n 項までの和  は

S_n = [ ヌ ]n/([ ネ ]n + [ ノ ])

であることが分かる。

第四問 (選択 20 点)

本問では vectors はすべて太字斜体を用いる。

座標空間に於いて, 立方体 OABC-DEFG の頂点を

O(0, 0, 0), A(3, 0, 0), B(3, 3, 0), C(0, 3, 0),
D(0, 0, 3), E(3, 0, 3), F(3, 3, 3), G(0, 3, 3)

 とし, OD を 2:1 に内分する点を K, OA を 1:2 に内分する点を L とする。 BF 上の点 M, FG 上の点 N 及び, K, L の四点は同一平面上にあり, 四角形 KLMN は平行四辺形であるとする。

(1) 四角形 KLMN の面積を求めようベクトル LK を成分で表すと

LK = ([ アイ ], [ ウ ], [ エ ])

 となり, 四角形 KLMN が平行四辺形であることにより LK = [ オ ] である。 [ オ ] に当てはまるものを, 次の 0 から 3 の内から一つ選べ。

0 ML
1 LM
2 NM
3 MN

ここで M(3, 3, s), N(t, 3, 3) と表すと, LK = [ オ ] であるので, s = [ カ ], t = [ キ ] となり, N は FG を 1: [ ク ] に内分することが分かる。

又 LK と LM について

LK・LM = [ ケ ], |LK| = √[ コ ], |LM| = √[ サシ ]

となるので, 四角形 KLMN の面積は √[ スセ ] である。

(2) 四角形 KLMN を含む平面を α 都市, 点 O を通り平面 α と垂直に交わる直線を l, α と l の交点を P とする。 |OP| と三角錐 OLMN の体積を求めよう。

P(p, q, r) とすると, OP は LK 及び LM と垂直であるから, OP・LK = OP・LM = [ ソ ] となるので, p = [ タ ]r, q = ([ チツ ]/[ テ ])r であることが分かる。 OP と PL が垂直であることにより r = [ ト ]/[ ナニ ] となり,  |OP| を求めると

 |OP| = ([ ヌ ] √[ ネノ ])/[ ハ ]

である。 |OP| は三角形 LMN を底面とする三角錐 OLMN の高さであるから, 三角錐 OLMN の体積は [ フ ] である。

第五問 (選択 20 点)

次の表は, あるクラスの生徒九人に対して行われた英語と数学のテスト (各二十点満点) の得点を纏めたものである。 但し, テストの得点は整数値である。 又, 表の数値はすべて正確な値であり, 四捨五入されていないものとする。

以下, 小数の形で解答する場合は, 指定された桁 (けた) 数の 一つ下の桁を四捨五入し, 解答せよ。 途中で割り切れた場合は, 指定された桁まで 0 にマークすること。

(1) 生徒 5 の英語の得点 A は [ アイ ] 点であり, 九人の英語の得点の分散 B の値は [ ウエ ].[ オカ ] である。 又, 九人の数学の得点の平均値が 15.0 であることと, 英語と数学の得点の相関係数が 0.500 であることから, 生徒 6 の数学の得点 C と生徒 7 の数学の得点 D の関係式

C + D = [ キク ]
C - D = [ ケ ]

が得られる。 従って, C は [ コサ ] 点, D は [ シス ] 点である。

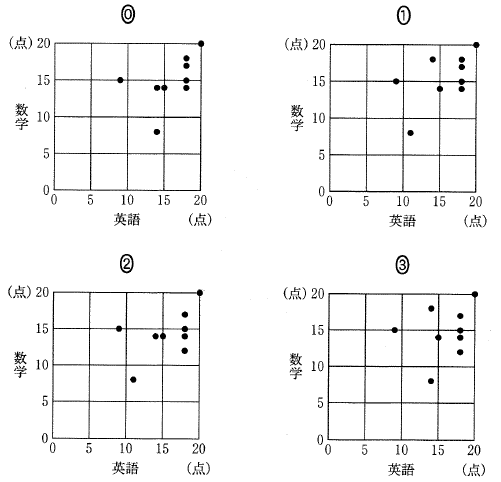
(2) 九人の英語と数学の得点の相関図 (散布図) として適切なものは [ セ ] である。 [ セ ] にてはまるものを, 次の 0 から 3 の内から一つ選べ。

(3) 生徒 10 が転入したので, その生徒に対して, 同じテストを行った。 次の表は, 初めの九人の生徒に, 生徒 10 を加えた十人の得点を纏めたものである。 但し, 表の数値は全て正確な値であり, 四捨五入されていないものとする。

十人の英語の得点の平均値 E は [ ソタ ].[ チ ] 点であり, 生徒 10 の数学の得点は [ ツ ] 点である。

(4) 生徒 10 が転入した後で, 一人の生徒が転出した。 残った九人の生徒について, 英語の得点の平均値は十人の平均値と同じ  [ ソタ ].[ チ ] 点, 数学の得点の平均値は十人の平均値と同じ 14.0 点であった。 転出したのは生徒 [ テ ] である。 又, 英語について, 十人の得点の分散の値を v, 残った九人の得点の分散の値を v' とすると

v'/v = [ ト ]

が成り立つ。 更に, 十人についての英語と数学の得点の相関係数の値を r, 残った九人についての英語と数学の得点の相関係数の値を r' とすると

r'/r = [ ナ ]

が成り立つ。  [ ト ], [ ナ ] に当てはまるものを, 次の 0 から 5 の内から一つずつ選べ。 但し, 同じものを選んでも良い。

0 -1
1 1
2 9/10
3 (9/20)²
4 10/9
5 (10/9)²

第六問 (選択 20 点)

2 以上の自然数 N に対して, 1 から N 迄の自然数の積

N = 1・2・…・N

の素因数分解を考える。

(1) N = 6 の時, N! の素因数分解は 6! = 2^{[ ア ]}・3^{[ イ ]}・5 である。 6! は素因数 2 を [ ア ] 個, 素因数 3 を [ イ ] 個, 素因数 5 を一個持つ。

(2) N! が持つ素因数 2 の個数を求める方法について考えよう。
先ず, N/2 の整数部分を M と置く。 N 以下の自然数の中には, M この偶数 2, 4, ..., 2M がある。 その他の奇数の積を Q と置くと, N! は次のように表すことが出来る。

N! = Q・2・4・…・2M = Q・2^M・M !

従って, N! は少なくとも M 個の素因数 2 を持つことが分かる。 更に, M ! が持つ素因数 2 の個数を求める為に, N! に対する手順を M ! に対して再び用いることが出来る。

つまり, N! が持つ素因数 2 の個数を求める為には, N から N/2 の整数部分である M を求め, M を改めて N と考えて, 同じ手順を用いて, 新しく M を求める, という手順の繰り返しを M < 2 となるまで行えば良い。 この手順の繰り返しで求められたすべての M の和が, N! が持つ素因数 2 の個数である。

例えば, N = 13 の場合には, 13/2 = 6.5 であるから, M = 6 となる。 この手順を繰り返して M を求めた結果は, N から M を求める手順を矢印 (→) で表すと, 次のように纏められる。

13→6→3→1

 太字で表された, 6, 3, 1 が, この手順を繰り返して求められた M の値である。 それらの和 6 + 3 + 1 = 10 が, 13! の持つ素因数 2 の個数である。

この手順に従って, 2 以上の自然数 N を入力して, N! が持つ素因数 2 の個数を出力する 〔プログラム 1〕 を作成した。 但し, INT(X) は X を超えない最大の整数を表す函数である。

〔プログラム 1〕

100 INPUT PROMPT "N = ": N
110 LET D = 2
120 LET C = 0
130 LET M = N
140 FOR J = 1 TO N
150    LET M = INT(M/D) 
160    LET [ ウ ]
170    LET [ エ ] THEN GOTO 190
180 NEXT J
190 PRINT "素因数 "; D; " は "; C; "個"
200 END

〔プログラム 1〕の [ ウ ] に当てはまるものを, 次の 0 から 8 の中から一つ選べ。

0 C = C + 1
1 C = M
2 C = C + M
3 C = C + M + 1

[ エ ] に当てはまるものを, 次の 0 から 4 の中から一つ選べ。

0 M >= D
1 M = D
2 M <= D
3 M < D
4 M > D

〔プログラム 1〕を実行し, 変数 N に 101 を入力する。 170 行の 「GOTO 190」 が実行される時の変数 J の値は [ オ ]  である。 又, 190 行で出力される変数 C の値は [ カキ ] である。

(3) N! が持つ素因数 2 の個数を求める方法は, 他の素因数の個数についても同様に適用出来る。 例えば N! が持つ素因数 5 の個数を求める場合は, 先ず, N/5 の整数部分を M と置く。 N 以下のに全数の中には M 個の 5 の倍数があるので, N! は少なくとも M この素因数 5 を持つ。 又, これらの M 個の 5 の倍数を 5 で割った商は 1, 2, ..., M である。 M! の中の素因数 5 の個数を求める為には, M を N と考えて, 同じ手順を繰り返せば良い。

従って, N! が持つ素因数 5 の個数を求める為には〔プログラム 1〕の [ クケコ ] 行を [ サ ] に変更すれば良い。 [ サ ] に当てはまるものを, 次の 0 から 5 の内から一つ選べ。

0 INPUT PROMPT "N = ": N
1 INPUT PROMPT "C = ": C
2 INPUT PROMPT "M = ": M
3 LET C = 5
4 LET D = 5
5 LET M = D

変更した〔プログラム 1〕を実行することにより, 2014! は素因数 5 を  [ シスセ ] 個持つことが分かる。

(4) N 以下の全ての素数が, N! の素因数として含まれる。 その個数は, 素数 2 や素数 5 の場合と同様に求められる。 N 以下の全ての素因数について, N! が持つ素因数とその個数を順に出力するように〔プログラム 1〕を変更して〔プログラム 2〕を作成した。 行番号に下線が引かれた行は, 変更または追加された行である。

但し, 繰り返し処理 「FOR K = A TO B 〜 NEXT K」に於いて, A が B より大きい場合, この繰り返し処理は実行されず次の処理に進む。

〔プログラム 2〕

100 INPUT PROMPT "N = ": N
110 FOR D = 2 TO N
111   FOR K = 2 TO D - 1
112     IF [ ツ ] THEN [ テ ]
113 　NEXT K
120 LET C = 0
130 LET M = N
140 FOR J = 1 TO N
150    LET M = INT(M/D) 
160    LET [ ウ ]
170    LET [ エ ] THEN GOTO 190
180 NEXT J
190 PRINT "素因数 "; D; " は "; C; "個"
191 NEXT D
200 END

〔プログラム 2〕の 111 行から 113 行までの処理は, D が素数であるかどうかを判定する為のものである。 [ ツ ], [ テ ] に当てはまるものを, 次の 0 から 8 の内から一つずつ選べ。 但し, 同じものを選んでも良い。

0 INT(D/K) = 1
1 INT(D/K) > 1
2 D = INT(D/K)*K
3 D <> INT(D/K)*K
4 GOTO 120
5 GOTO 130
6 GOTO 180
7 GOTO 190
8 GOTO 191

〔プログラム 2〕を実行し, 変数 N に 26 を入力した時, 190 行は [ ト ] 回実行される。 [ ト ] 回 の内, 変数 C の値が 2 となるのは [ ナ ] 回である。

解答へ。

センター試験の目次に戻る。