第一問 (必答 30 点)
[1] (1) $\ds{8^{5\over6}=\left(2^3\right)^{5\over6} = 2^{3\cdot{5\over6}}= 2^{5\over2} = 2^{2 +{1\over2}} = 2^2\cdot2^{1\over2} = 4\sqrt{2}}$. (2 点)
$\log_{27}\ds{1\over9} = \log_{27}1 -\log_{27}9 = -\ds{{\log_3 9}\over\log_3
27} = -\ds{{\log_3 3^2}\over\log_3 3^3} =\ds{-2\over3}$. (2 点)
(2) $y
= \ds{\left({1\over2}\right)}^x = 2^{-x}$ より $y$ 軸対称なので カ は 2 (1
点)
$y =2^x$ と $y = \log_2 x$ は互いに逆函数なので, 直線 $y=x$ に関して対称。 つまり キ は 3. (1 点)
$y=\log_{1\over2}x$$=\ds{{\log_2 x}\over\log_2\ds{1\over2}} = -\log_2 x$ なので,
$x$ 軸対称。 つまり ク は 1. (1 点)
$y = \log_2\ds{1\over x}=\log_2x^{-1} = -\log_2 x$ より, こちらも $x$ 軸対称。 つまり ケ も
1. (1 点)
(3) $y = \left(\log_2x-\log_24\right)^2 - 4\cdot\ds{{\log_2x}\over\log_24}+3$
$=\left(\log_2x-\log_22^2\right)^2 - 4\cdot\ds{{\log_2x}\over\log_22^2}+3$
$=\left(\log_2x-2\right)^2 - 4\cdot\ds{{\log_2x}\over2}+3$
$=\left(\log_2x\right)^2 - 4\log_2x+4-2\log_2x+3$
$=\left(\log_2x\right)^2 - 6\log_2x+7$
$=t^2 - 6t + 7$. (2 点)
$x > 0$ の時, $t = \log_2x$ は実数全体を取るので, シ は 3. (2 点)
$y = (t - 3)^2 - 2$ なので
$t = 3$ 即ち $\log_2x=3=3\cdot\log_22=\log_22^3 =\log_28$. つまり $x = 8$ の時 (ここまで 2
点)
最小値 $-2$ を採る。 (1 点)
基本的で難しくないと思われる。
グラフの対称性はある程度基本を押さえておかないと出来なかっただろうか。
[2] (1) $\left(\cos^2x -
\sin^2x\right)\sin^2x\cos^2x + k\left(\sin^2x-\cos^2x\right)=0$
$\cos2x\cdot\sin^2x\cos^2x - k\cos2x = 0$
$\cos2x\left(\sin^2x\cos^2x - k\right)=0$
$\cos2x\left(\left(\sin x\cos x\right)^2 - k\right)=0$
$\cos2x\left(\left(\ds{{2\sin x\cos x}\over2}\right)^2 - k\right)=0$
$\cos2x\left(\left(\ds{{\sin2x}\over2}\right)^2 - k\right)=0$
$\left(\ds{{\sin^2 2x}\over4} - k\right)\cos2x=0$ (3 点)
$0 < x < \ds{\pi\over2}$ で $\cos2x = 0$ とすると ($0 < 2x < \pi$ だから) $2x = \ds{\pi\over2}$ $\therefore x = \ds{\pi\over4}$ (2 点)
従って $0 < x < \ds{\pi\over2}$ で ($0 < 2x < \pi$ なので) $0 < \sin^2 2x \leqq1$
だから $4k > 1$ 即ち $k > \ds{1\over4}$ (2 点) の時は, 上の解のみである。
$0 < k <
\ds{1\over4}$ の時は $\sin^2 2x = 4k$ で, $0 < 2x < \pi$ より $\sin2x > 0$ であるから
$\sin2x = 2\sqrt{k}$. この解は二つあるので, 上記の解と合わせて合計 3 個。 (3 点)
一方
$k = \ds{1\over4}$ の時は $x = \ds{\pi\over4}$ となって, 上記の解と同じなので, 解は 1
個。 (2 点)
(2) $\sin2x = 2\sqrt{k} = 2\cdot\ds{2\over5} = \ds{4\over5}$. (1 点)
$\sin^22x+\cos^22x = 1$ なので
\begin{align}
\cos^22x &=1-\sin^22x \\
&= 1-\ds{16\over25} = \ds{9\over25}.
\end{align}
$\ds{\pi\over4} < x < \ds{\pi\over2}$ なので, $\ds{\pi\over2} < 2x < \pi$ だから,
$\cos2x < 0$ 即ち $\cos2x = \ds{-3\over5}$. (1 点)
$\cos2x = 2\cos^2x - 1 = -\ds{3\over5}$
$2\cos^2x= 1 - \ds{3\over5} = \ds{2\over5}$
$\cos^2x=\ds{1\over5}$.
$\ds{\pi\over4} < x < \ds{\pi\over2}$ なので $\cos x > 0$ つまり $\cos x =
\ds{1\over\sqrt5} =\ds{\sqrt{5}\over5}$. (2 点)
[2] の (1) の式変形は基本的だが, 解を求める際に, $\cos2x$ から出てくる方を数え忘れそうになるので注意。
(実際自分は一回忘れた)
もしかしたら意図的なひっかけ問題なのかもしれない。
第二問 (必答 30 点)
(1) $C_1$ と $C_2$ は交わらないので (実際 $\left({1\over2}x^2+{1\over2}\right)-{1\over4}x^2 = {1\over4}x^2+{1\over2} \geqq{1\over2}$ で $C_1$ の方が常に上にあるから) \begin{eqnarray*} S &=&\int_a^{a + 1} \left({1\over2}x^2+{1\over2}-{1\over4}x^2\right)dx \\ &=&\int_a^{a + 1} \left({1\over4}x^2+{1\over2}\right)dx \hspace{4em} (両方で 2 点) \\ &=&{1\over4}\int_a^{a + 1} \left(x^2+2\right)dx \\ &=&{1\over4}\left[{1\over3}x^3+2x\right]_a^{a+1}\\ &=&{1\over4}\left({1\over3}(a+1)^3+2(a+1) - \left({1\over3}a^3 + 2a\right)\right)\\ &=&{1\over4}\left({1\over3}\left((a+1)^3-a^3\right) + 2a+2-2a\right)\\ &=&{1\over4}\left({1\over3}(3a^2+3a+1)+2\right)\\ &=&{1\over4}\left(a^2+a+{1\over3}+2\right)\\ &=&{1\over4}\left(a^2+a+{7\over3}\right)\\ &=&{a^2\over4}+{a\over4}+{7\over12}. \end{eqnarray*}(最後の定数項以外が両方出来て 3 点, 定数項は単独で 3 点)
更に計算を進めて \begin{eqnarray*} S &=& {1\over4}\left(a^2+a\right)+{7\over12}\\ &=& {1\over4}\left(\left(a+{1\over2}\right)^2 - {1\over4}\right)+{7\over12}\\ &=& {1\over4}\left(a+{1\over2}\right)^2 - {1\over16}+{7\over12}\\ &=& {1\over4}\left(a+{1\over2}\right)^2 + {-3+28\over48}\\ &=& {1\over4}\left(a+{1\over2}\right)^2 + {25\over48}\\ \end{eqnarray*} だから $S$ は $a=\ds{-1\over2}$ (2点) の時最小値 $\ds{25\over48}$ を取る。 (3 点)
(2) 図を描くと

$\ds{{1\over2}x^2 + {1\over2} = 1}$ と置くと $x^2 + 1 = 2$ だから $x^2 = 1$. 従って $x = \pm1$. (2 点)
又今度は $\ds{{1\over4}x^2= 1}$ と置くと $x=\pm2$. (1 点).
従って $0 \leqq a \leqq2$ (2 点) ならば $T > 0$.
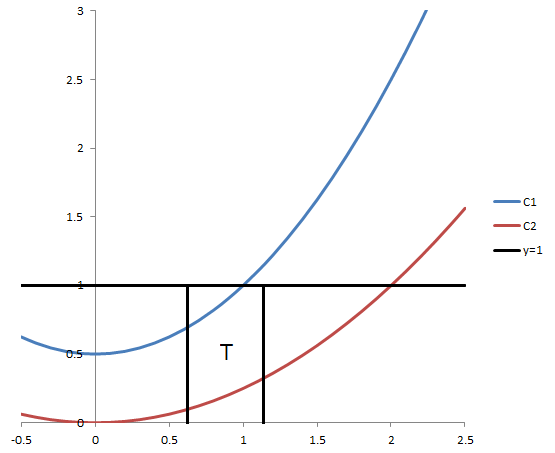
$1\leqq a\leqq2$ の場合, ($C_1$ は T から外れて, $C_2$ が単調増加だから) $a$ が増加すると $T$ は減少するので ツ は
1. (2 点)
従って $T$ が最大になるのは $0\leqq a\leqq1$ の範囲である。
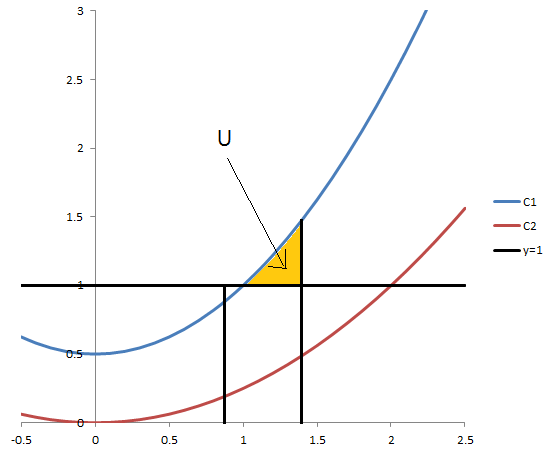
(最後の分母が各 2 点)
\begin{eqnarray*} \therefore T &=& S-U\\ &=& {a^2\over4} +{a\over4} + {7\over12} - \left({a^3\over6}+{a^2\over2}\right)\\ &=& -{a^3\over6} +\left({1\over4}-{1\over2}\right)a^2+{a\over4} + {7\over12}\\ &=& -{a^3\over6} -{a^2\over4}+{a\over4} + {7\over12}\\ \end{eqnarray*}(全部出来て 3 点)
ここで $\ds{{dT\over da} = -{a^2\over2} - {a\over2} + {1\over4} =
-{1\over4}\left(2a^2 + 2a - 1\right) = 0}$ と置くと,\[a={-1\pm\sqrt{1 + 2}\over2} = {-1\pm\sqrt3\over2}\]
$0\leqq a \leqq 1$ だったので (実際 1 < 3 < 9 より, $1 < \sqrt3 < 3$ だから $0 < -1+\sqrt3 <
2$. 従って $0 < {-1+\sqrt{3}\over2} < 1$)
|
$a$ |
+0 | $\hspace{2em}\cdots\hspace{2em}$ | $\ds{-1+\sqrt{3}\over2}$ | $\hspace{2em}\cdots\hspace{2em}$ | $1-0$ |
| $\ds{dT\over da}$ | $\ds{\left({1\over4}\right)}$ | + | 0 | - | $\ds{\left(-{3\over4}\right)}$ |
| $T$ | $\nearrow$ | 極大 | $\searrow$ |
従って, $T$ は $a = \ds{-1+\sqrt{3}\over2}$ (3 点) で最大値を持つことが分かる。
図を描きながらやればよい。 私はうっかりして U の面積を求める時に 1 を引くのを忘れて難儀した。
第三問 (選択 20 点)
(1) 順番に考えると
\begin{array}{ccc} 分母 & 個数 & 合計 \\ 2 & 1 & 1\\ 3 & 2 & 3\\ 4 & 3 & 6\\ 5 & 4 & 10\\ 6 & 5 & 15 \end{array}なので, 15 番目の分母は 6 であり, その五番目であることが分かるから $a_{15} = \ds{5\over6}$. (2 点)
$\ds{1\over8}$ は (分母が 7 までのものの次だから) $\ds{\sum_{k=1}^6k + 1 = {6\cdot7\over2} + 1 = 22}$. (2 点)
(2) 上記と同様に考えて
\begin{eqnarray*} M_k &=& \sum_{i=1}^{k-1}i + 1 = {(k-2)(k-1)\over2} + 1\\ &=& {k^2-3k+2\over2} + 1\\ &=& {1\over2}k^2 - {3\over2}k + 2. \end{eqnarray*}(2 点)
$\ds{N_k =\sum_{i=1}^{k-1}i={k(k-1)\over2} = {1\over2}k^2 -{1\over2}k}$. (2
点)
さて今 $M_k \leqq104\leqq N_k$ と置く。
この時
$\ds{{1\over2}\left(k^2-3k+4\right)\leqq104\leqq{1\over2}\left(k^2-k\right)}$
$k^2-3k+4\leqq208\leqq k^2-k=k(k-1)$.
さて今ここで 208 を素因数分解してみると $208 = 2^4\cdot13 = 13\cdot16$ なので,
最後の不等式の右辺だけを考えてみると,
$k=13\Longrightarrow 右辺=13\cdot12=156$,
$k=14\Longrightarrow 右辺=14\cdot13=182$,
$k=15\Longrightarrow 右辺=15\cdot14=15\cdot2\cdot7=30\cdot7=210$.
だから, この不等式を満たす整数は $k=15$ で
$\ds{M_{15}={13\cdot14\over2} + 1 = 91 + 1 = 92}$.
そして $104 - 92 + 1 = 13$
なので, $a_{104}=\ds{13\over15}$. (4 点).
(3) $\ds{\{a_k\}}$ の決め方から
$\ds{\sum_{i=M_k}^{N_k}a_i = {1\over k}\sum_{i=1}^{k-1}i = {1\over
k}\cdot{1\over2}(k-1)k = {1\over2}k-{1\over2}}$. (2 点)
従って
(2 点).
さて又 $a_{104}=\ds{13\over15}$ であることから $a_{103}=\ds{12\over15}$ である。 従って
\begin{eqnarray*} \sum_{n=1}^{103}a_n &=& \sum_{n=1}^{N_{14}} a_n + {1\over15}(1 + 2 + 3 + \cdots + 12)\\ &=& {1\over4}\cdot14\cdot13+{1\over15}\cdot{1\over2}\cdot12\cdot13\\ &=& {7\cdot13\over2}+{2\cdot13\over5} = 13\cdot\left({7\over2}+{2\over5}\right)\\ &=& 13\cdot{35+4\over10}={13\cdot39\over10}={507\over10}. \end{eqnarray*}(4 点)
分母の $k$ と和の上端 (上限) のずれを間違えなければ難しくはないと思うがどうか。
今年一番難しかったのが本問かもしれない。
第四問 (選択 20 点)
(1) $\vec a\cdot\vec b =\overrightarrow{OA}\cdot\overrightarrow{OB} =\left|\overrightarrow{OA}\right|\left|\overrightarrow{OB}\right|\cos\angle AOB = 3\cdot2\cos60^\circ=3\cdot2\cdot\ds{1\over2} = 3$. (1 点)
$\vec b\cdot\vec c =\overrightarrow{OB}\cdot\overrightarrow{OC} =\left|\overrightarrow{OB}\right|\left|\overrightarrow{OC}\right|\cos\angle AOB = 2\cdot2\cos60^\circ=2\cdot2\cdot\ds{1\over2} = 2$. (1 点)
\begin{eqnarray*} \left|\overrightarrow{PQ}\right|^2 &=& \left|\overrightarrow{OQ}-\overrightarrow{OP}\right|^2\\ &=& \left|(1-t)\vec b + t\vec c - s\vec a\right|^2 \\ &=& \left|-s\vec a + \left(\vec c-\vec b\right)t + \vec b\right|^2\\ &=& \left|\vec a\right|^2s^2 + \left|\vec c - \vec b\right|^2t^2-2st\vec a\cdot\left(\vec c - \vec b\right) -2s\vec a\cdot\vec b +2t\vec b\cdot\left(\vec c - \vec b\right) + \left|\vec b\right|^2 \\ &=& 9s^2 + \left(\left|\vec c\right|^2 - 2\vec c\cdot\vec b +\left|\vec b\right|^2\right)t^2 - 2st\left(\vec a\cdot\vec c - \vec a\cdot\vec b\right) -2s\cdot3 + 2t\left(\vec b\cdot\vec c - \left|\vec b\right|^2\right) + 4\\ &=& 9s^2 + (4 - 4 + 4)t^2 - 6s + 2t(2 - 4) + 4\\ &=& 9s^2 + 4t^2 - 6s - 4t + 4\\ &=& (3s - 1)^2 + (2t-1)^2 + 2. \end{eqnarray*}($s$ の括弧内が 2 点, $t$ の括弧内も 2 点, 定数項が 1 点)
従って, $\ds{\left|\overrightarrow{PQ}\right|}$ が最小になるのは $s =\ds{1\over3}$ (1 点), $t=\ds{1\over2}$ (1 点) の時であり, この時 $\ds{\left|\overrightarrow{PQ}\right|=\sqrt2}$ (1 点) となる。
(3) $s =\ds{1\over3}$, $t=\ds{1\over2}$ の時なので
$\overrightarrow{PQ}=\overrightarrow{OQ}-\overrightarrow{OP} =
\ds{-{1\over3}\vec a + {1\over2}\vec b+ {1\over2}\vec c}$.
(1 点)
で, $P$ は辺 $OA$ 上にあるので $\angle APQ = 90^\circ$. (1 点)
従って $\triangle APQ =
\ds{{1\over2}\left|\overrightarrow{AP}\right|\left|\overrightarrow{PQ}\right|} =
\ds{{1\over2}\cdot\left({2\over3}\cdot3\right)\cdot\sqrt{2}=\sqrt2}$. (2 点)
さて又,
$\ds{\overrightarrow{OG}={1\over3}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)
= {1\over3}\left(\vec a + \vec b + \vec c\right)}$ であり一方
$\ds{\overrightarrow{OQ}={1\over2}\vec b+{1\over2}\vec c}$ から $\vec b + \vec c =
2\overrightarrow{OQ}$.
従って
従って (内分点の公式から) $G$ は $AQ$ を $2:1$ に内分する点である。 (2 点)
更に $\ds{\triangle GPQ = {1\over3}\triangle APQ = {\sqrt{2}\over3}}$ (2 点)
それ程難しくないと思ったがどうでしょうか。
第五問 (選択 20 点)
(1) $n = 2$ なので $X=-2, 2, 6$. (この順で 1 点)
確率は順に
$\ds{\left({2\over3}\right)^2={4\over9}}$. (1 点)
$\ds{2\cdot{1\over3}\cdot{2\over3}={4\over9}}$. (1 点)
$\ds{\left({1\over3}\right)^2={1\over9}}$. (1 点)
(2) $n$ 回移動すると $X = 3Y-(n-Y) = -n + 4Y$. (1 点)
二項分布なので $E(Y) = np$ だから コ は 0. (1 点)
$V(Y)=np(1-p)$ だから サ
は 1. (1 点)
$E(X) = E(-n + 4Y) = -n + 4E(Y) = -n + 4np = 4np
- n$ だから シ は 9. (1 点)
$V(X)=V(-n + 4Y) = 4^2V(Y) =
16np(1-p)$. だから ス は 8. (2 点)
(3) $E(Y)=\ds{1200\cdot{1\over4}} = 300$. (1 点)
$V(Y)= \ds{1200\cdot{1\over4}\cdot{3\over4}=300\cdot{3\over4}={900\over4}}$ なので
$\sigma(Y)=\ds{{30\over2}= 15}$. (1 点)
一方 $X \geqq120$.
即ち $-1200 + 4Y \geqq 120$.
$4Y\geqq1320$
$Y\geqq330$
$Y-300\geqq30$
$\ds{Y-300\over15}\geqq2.00$. (2 点)
正規分布表に拠れば $P\left(0.5\leqq z_0\leqq2.00\right) = 0.4772$ であるから,
$0.5 - 0.4772 = 0.0228\fallingdotseq0.023$. だから ニヌネ は 023.
(2 点)
(4) $X = -n + 4Y$ なので
\[ y={x+n\over4}={1440+2400\over4}=960. \]$r =\ds{{y\over n}={960\over2400} ={6\over15}={2\over5}}$.
$v = \ds{{p(1-p)\over n} = {\ds{2\over5}\cdot\ds{3\over5}\over2400} =
{6\over2400\cdot5\cdot5}={1\over10000}}$.
$\therefore\sigma=\ds{1\over100}$.
従って, 正規分布表から (片側 $0.95\div2=0.475$ の所を見て), 正規化した $\ds{p-r\over\sigma}$ の値の範囲が
$-1.96\leqq\ds{\ p-\ds{2\over5}\ \over\ds{1\over100}}\leqq1.96$ となるので,
$-0.0196\leqq p-0.4\leqq0.0196$
$0.4-0.0196\leqq p\leqq0.4+0.0196$
$0.3804\leqq p\leqq0.4196$
だから小数第四位を四捨五入して
$0.380\leqq p\leqq0.420$ (各々 2 点)
誘導されているので, 難しくはないと思われる。
二項分布や期待値 (平均), 分散の計算の仕方と, 推計では正規化がきちんとできるかどうかが key point ではないかと思われる。
センター試験の目次に戻る。