Sunday, 17th January, 2016.
11:20 -- 12:20 (1hr)
平均: 56.66 (中間集計)
55.27 (本集計)
第一問 (必答 30 点)
[1] $a$ を実数とする。 $x$ の関数 \[f(x) = (1+2a)(1 - x) + (2 - a)x\] を考える。\[f(x) = (-[\ ア\ ]a+[\ イ\ ])x + 2a + 1 \]である。
(1) $0\leqq x\leqq 1$ に於ける $f(x)$ の最小値は,
$a\geqq\ds{[\ イ\ ]\over[\ ア\ ]}$
の時, $[\ ウ\ ]a + [\ エ\ ]$ であり,
$a > \ds{[\ イ\ ]\over[\ ア\ ]}$ の時, $[\ オ\ ]a
+[\ カ\ ]$ である。
(2) $0\leqq x\leqq 1$ に於いて, 常に $f(x)\geqq\ds{2(a+2)\over3}$ となる $a$ の値の範囲は,
$\ds{{[\ キ\ ]\over[\ ク\ ]}\leqq a\leqq{[\ ケ\ ]\over[\ コ\ ]}}$ である。
[2] 次の問に答えよ。 必要ならば, $\sqrt{7\,}$ が無理数であることを用いて良い。
(1) $A$ A を有理数全体の集合, $B$ を無理数全体の集合とする。 空集合を $\varnothing$ と表す。
次の
(i)--(iv) が真の命題になるように [ サ ]--[ セ ] に当てはまるものを, 下の 0--5
の内から一つずつ選べ。 但し, 同じものを繰り返し選んでも良い。
(i) $A$ [ サ ] $\{0\}$。
(ii) $\sqrt{28\,}$ [ シ ] $B$.
(iii) $A = \{0\}$
[ ス ] $A$.
(iv) $\varnothing =A$ [ セ ] $B$.
0 $\in$
1 $\ni$
2
$\subset$
3 $\supset$
4 $\cap$
5 $\cup$
(2) 実数 $x$ に対する条件 $p$, $q$, $r$ を次の様に定める。
$p$: $x$ は無理数
$q$: $x +\sqrt{28\,}$ は有理数
$r$: $\sqrt{28\,}x$ は有理数。
次の [ ソ ], [ タ ] に当てはまるものを, 下の 0 から 3 の内から一つずつ選べ。 但し, 同じものを繰り返し選んでも良い。
$p$ は $q$ である為の [ ソ ]
$p$ は $q$ である為の [ タ ]
0 必要十分条件である
1 必要条件であるが, 十分条件ではない
2 十分条件であるが, 必要条件ではない
3 必要条件でも十分条件でもない
[3] $a$ を $1$ 以上の定数とし, $x$ についての連立不等式
\begin{eqnarray} \left\{ \begin{array}{2} x^2 + (20-a^2)x - 20a^2 \leqq 0 &\cdots\cdots\cdots\cdots①\\ x^2 + 4ax \geqq 0 \hfill&\cdots\cdots\cdots\cdots② \end{array} \right. \end{eqnarray}を考える。 この時, 不等式 ① の解は [ チツテ ] $\leqq x\leqq a^2$ である。 又, 不等式 ② の解は $x \leqq [\ トナ\ ]a$, $[\ ニ\ ]\leqq x$ である。
この連立不等式を満たす負の実数が存在するような $a$ の値の範囲は
\[ 1\leqq a \leqq [\ ヌ\ ] \]である。
第二問 (必答 30 点)
[1] $\triangle ABC$ の辺の長さと角の大きさを測った所, $AB = 7\sqrt{3\,}$ 及び $\angle ACB = 60^\circ$ であった。 従って, $\triangle ABC$ の外接円 $O$ の半径は [ ア ] である。
外接円 $O$ の, 点 $C$ を含む弧 $AB$ 上で点 $P$ を動かす。
(1) $2PA = 3PB$ となるのは $PA = [\ イ\ ]\sqrt{[\ ウエ\ ]\ }$ の時である。
となる。 更に, G が点 (1, 2b - 1) を通る時
(2) $\triangle PAB$ の面積が最大となるのは $PA = [\ オ\ ]\sqrt{[\ カ\ ]\ }$ の時である。
(3) $\sin\angle PBA$ の値が最大となるのは $PA = [\ キク\ ]$ の時であり, この時 $\triangle PAB$ の面積は $\ds{[\ ケコ\ ]\sqrt{[\ サ\ ]\ }\over[\ シ\ ]}$ である。
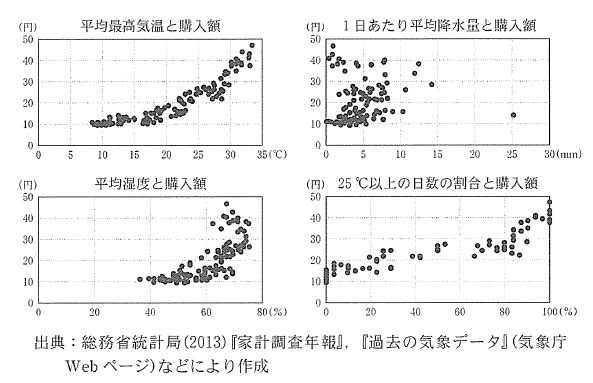
[2] 次の四つの散布図は, 2003 年から 2012 年までの 120 ヶ月の東京の月別 data を纏めたものである。 それぞれ, 一日の最高気温の月平均 (以下, 平均最高気温), 一日当たりの平均降水量, 平均湿度, 最高気温 25 ℃ 以上の日数の割合を横軸に取り, 各世帯の一日当たりアイスクリーム平均購入額 (以下, 購入額) を縦軸としてある。

次の [ ス ], [ セ ] に当てはまるものを, 下の 0 から 4 の内から一つずつ選べ。 但し, 解答の順序は問わない。
これらの散布図から読み取れることとして正しいものは [ ス ] と [ セ ] である。
0 平均最高気温が高くなるほど購入額は増加する傾向がある。
1
一日当たり平均降水量が多くなるほど購入額は増加する傾向がある。
2
平均湿度が高くなるほど購入額の散らばりは小さくなる傾向がある。
3 25 ℃ 以上の日数の割合が 80 % 未満の月は,
購入額が 30 円を超えていない。
4 この中で正の相関があるのは, 平均湿度と購入額の間のみである。
[3] 世界四都市 (東京, O 市, N 市, M 市) の 2013 年の 365 日の各日の最高気温の data について考える。
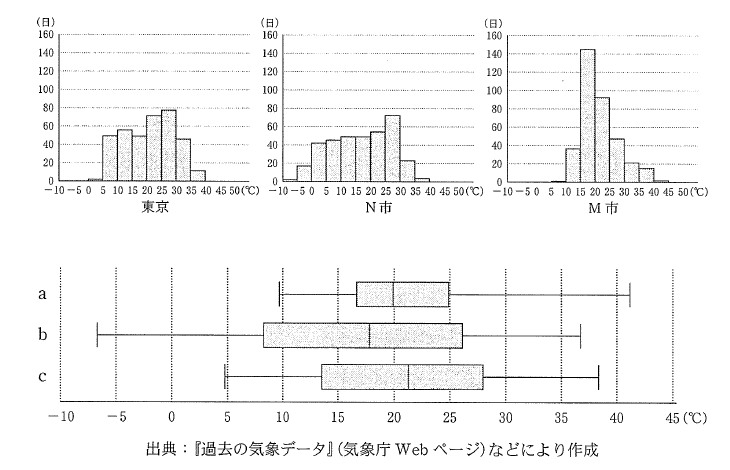
(1) 次のヒストグラムは, 東京, N 市, M 市の data を纏めたもので, この三都市の箱ひげ図は下の a, b, c の何れかである。
次の [ ソ ] に当てはまるものを, 下の 0 から 5 の内から一つ選べ。
都市名と箱ひげ図の組み合わせとして正しいものは [ ソ ] である。
0 東京 - a, N 市 - b, M 市 - c.
1 東京
- a, N 市 - c, M 市 - b.
2 東京 - b, N 市 - a, M 市 - c.
3 東京 - b, N 市 - c, M 市 - a.
4 東京
- c, N 市 - a, M 市 - b.
5 東京 - c, N 市 - b, M 市 - a.
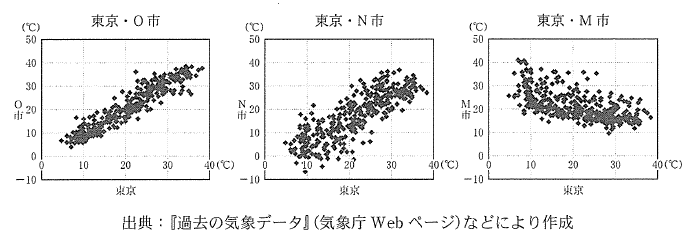
(2) 次の三つの散布図は, 東京, O 市, N 市, M 市の 2013 年の 365 日の各日の最高気温の data を纏めたものである。 それぞれ O 市, N 市, M 市の最高気温を縦軸にとり, 東京の最高気温を横軸にとってある。
次の [ タ ], [ チ ] に当てはまるものを, 下の 0 から 4 の内から一つずつ選べ。 但し, 解答の順序は問わない。
これらの散布図から読み取れることとして正しいものは, [ タ ] と [ チ ] である。
0 東京と N 市, 東京と M 市の最高気温の間にはそれぞれ正の相関がある。
1
東京と N 市の最高気温の間には正の相関, 東京と M 市の最高気温の間には負の相関がある。
2 東京と N
市の最高気温の間には負の相関, 東京と M 市の最高気温の間には正の相関がある。
3 東京と O
市の最高気温の間の相関の方が, 東京と N 市の最高気温の間の相関より強い。
4 東京と O
市の最高気温の間の相関の方が, 東京と N 市の最高気温の間の相関より弱い。
(3) 次の [ ツ ], [ テ ], [ ト ] に当てはまるものを, 下の 0 から 9 の内から一つずつ選べ。 但し, 同じものを繰り返し選んでも良い。
N 市では温度の単位として摂氏 (℃) の他に華氏 (${}^\circ\rm{F}$) も使われている。 華氏 (${}^\circ\rm{F}$)
での温度は, 摂氏 (℃) での温度を $\ds{9\over5}$ 倍し, 32 を加えると得られる。 例えば, 摂氏 10 ℃ は,
$\ds{9\over5}$ 倍し, 32 を加える事で華氏 $50\ ^\circ\rm{F}$ となる。
従って, N 市の最高気温について,
摂氏での分散を $X$, 華氏での分散を $Y$ とすると, $\ds{Y\over X}$ は [ ツ ] になる。
東京 (摂氏) と
N 市 (摂氏) の共分散を $Z$, 東京 (華氏) と N 市 (華氏) の共分散を $W$ とすると, $\ds{W\over Z}$ は [ テ ]
になる (但し, 共分散は二つの変量のそれぞれの偏差の積の平均値)。
東京 (摂氏) と N 市 (摂氏) の相関係数を $U$, 東京 (華氏) と N
市 (華氏) の相関係数を $V$ とすると, $\ds{V\over U}$ は [ ト ]
になる。
0 $\ds{-{81\over25}}$
1
$\ds{-{9\over5}}$
2 $-1$
3
$\ds{-{5\over9}}$
4 $\ds{-{25\over81}}$
5
$\ds{{25\over81}}$
6 $\ds{{5\over9}}$
7
$1$
8 $\ds{{9\over5}}$
9
$\ds{{81\over25}}$
第三問から第五問は, 何れか二問を選択し, 解答しなさい。
第三問 (選択 20 点)
赤球四個, 青球三個, 白球五個, 合計十二個の球がある。 これら十二個の球を袋の中に入れ, この袋から $A$ さんが先ず一個取出し, その球を元に戻さずに続いて $B$ さんが一個取り出す。
(1) $A$ さんと $B$ さんが取り出した二個の球の中に, 赤球か青球が少なくとも一個含まれている確率は $\ds{[\ アイ\ ]\over[\ ウエ\ ]}$ である。
(2) $A$ さんが赤球を取り出し, 且つ $B$ さんが白球を取り出す確率は $\ds{[\ オ\ ]\over[\ カキ\ ]}$ である。 これより, $A$ さんが取り出した球が赤球であった時, $B$ さんが取り出した球が白球である条件付き確率は $\ds{[\ ク\ ]\over[\ ケコ \ ]}$ である。
(3) $A$ さんは一球取り出した後, その色を見ずに pocket の中にしまった。 $B$ さんが取り出した球が白球であることが分かった時, $A$ さんが取り出した球も白球であった条件付き確率を求めたい。
$A$ さんが赤球を取出し, 且つ $B$ さんが白球を取り出す確率は $\ds{[\ オ\ ]\over[\ カキ\ ]}$ であり, $A$ さんが青球を取出し, 且つ $B$ さんが白球を取り出す確率は $\ds{[\ サ\ ]\over[\ シス\ ]}$ である。 同様に, $A$ さんが白球を取出し, 且つ $B$ さんが白球を取り出す確率を求めることが出来, これらの事象は互いに背反であるから, $B$ さんが白球を取り出す確率は $\ds{[\ セ\ ]\over[\ ソタ\ ]}$ である。
よって, 求める条件付き確率は $\ds{[\ チ\ ]\over[\ ツテ\ ] }$ である。
第四問 (選択 20 点)
(1) 不定方程式 \[ 92x + 197y = 1 \] を満たす整数 $x$, $y$ の組の中で, $x$ の絶対値が最小のものは \[ x = [\ アイ\ ],\ y = [\ ウエ\ ] \] である。 不定方程式 \[ 92x + 197y = 10\] を満たす整数 $x$, $y$ の組の中で, $x$ の絶対値が最小のものは \[ x = [\ オカキ \ ],\ y = [\ クケ\ ] \] である。
以下では, 一個の骰子を八回繰り返して投げる。
(2) 二進法で 11011(2) と表される数を四進法で表すと [ コサシ ](4) である。
次の 0 から 5 の六進法の小数の内, 十進法で表すと有限小数として表せるのは, [ ス ], [ セ ]. [ ソ ] である。 但し, 解答の順序は問わない。等しいものは [ ] と [ ] である。 但し[ サ ] と [ シ ] は解答の順序を問わない。
0 0.3(6)
1 0.4(6)
2 0.33(6)
3 0.43(6) 4 0.033(6)
5 0.043(6)
第五問 (選択 20 点)
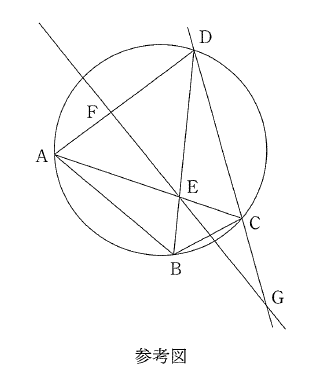
四角形 $ABCD$ に於いて, $AB = 4$, $BC =2$, $DA=DC$ であり, 四つの頂点 $A$, $B$, $C$, $D$ は同一円周上にある。 対角線 $AC$ と対角線 $BD$ の交点を $E$, 線分 $AD$ を $2:3$ の比内分する点を $F$, 直線 $FE$ と直線 $DC$ の交点を $G$ とする。
次の [ ア ] には下の 0 から 4 の内から当てはまるものを一つ選べ。
$\angle ABC$ の大きさが変化する時四角形 $ABCD$ の外接円の大きさも変化することに注意すると, $\angle ABC$ の大きさが幾らであっても, $\angle DAC$ と大きさが等しい角は, $\angle DCA$ と $\angle DBC$ と [ ア ] である。
0 $\angle ABD$ 1 $\angle ACB$ 2 $\angle ACB$ 3 $\angle BCG$ 4 $\angle BEG$
この事より $\ds{{EC\over AE}={[ イ ]\over[ ウ ]}}$ である。 次に, $\triangle ACD$ と直線 $FE$ に着目すると, $\ds{{GC\over DG}={[ エ ]\over[ オ ]}}$
(1) 直線 $AB$ が点 $G$ を通る場合について考える。
この時, $\triangle AGD$ の辺 $AG$ 上に点 $B$
があるので, $BG=[\ カ\ ]$ である。
又, 直線 $AB$ と直線 $DC$ が点 $G$ で交わり, 四点 $A$, $B$, $C$,
$D$ は同一円周上にあるので, $DC=[\ キ\ ]\sqrt{[\ ク\ ]}$ である。
(2) 四角形 $ABCD$ の外接円の直径が最小となる場合について考える。
この時, 四角形 $ABCD の外接円の直径は [ ケ
] であり, $\angle BAC=[\ コサ\ ]^\circ$ である。
又, 直線 $FE$ と直線 $AB$ の交点を $H$
とするとき, $\ds{{GC\over DG} = {[\ エ\ ]\over[\ オ\ ]}}$ の関係に着目して $AH$ を求めると, $AH=[\
シ\ ]$ である。
解答へ。
センター試験の目次に戻る。