(1) $\ds{AD\over DE}=\ds{1\over2}$.
Menelaus の定理より
$\ds{BP\over AP}\times\ds{FE\over BF}\times\ds{DA\over ED}=1$.
故に
$\ds{BP\over AP} = \ds{ED\over DA}\times\ds{BF\over FE} =2\times\ds{BF\over FE}$.
又, 同様にして $\ds{CQ\over AQ}\times\ds{FE\over CF}\times\ds{DA\over ED}=1$.
故に
$\ds{CQ\over AQ}=\ds{ED\over DA}\times\ds{CF\over EF} = 2\times\ds{CF\over EF}$.
以上より
$\ds{BP\over AP} + \ds{CQ\over AQ}$
$=2\times\ds{BF+CF\over EF}$
$=2\times\ds{BE+EC + 2CF)\over EF}$
$=2\times\ds{2(EC +CF)\over EF}$
$=4\times\ds{EF\over EF} = 4$.
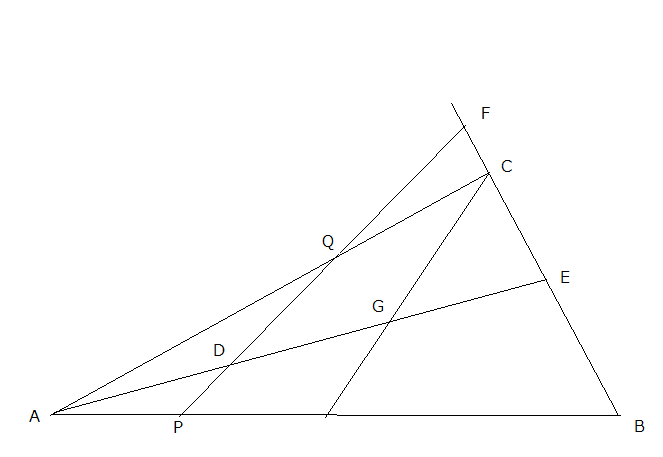
(2) 四点 $B$, $C$, $P$, $Q$ が同一円周上にあるとすると,
$\triangle APQ$ ∽ $\triangle ACB$ より
$AP:AQ = AC:AB = 6:9=2:3$
だから
$AQ =\ds{3\over2}AP$.
(方
ここで (1) の最後の式から
$4=\ds{BP\over AP} + \ds{CQ\over AQ}$
$= \ds{9-AP\over AP} + \ds{6-AQ\over AQ}$.
$= \ds{9\over AP} -1 + \ds{6\over AQ} -1$.
$6= \ds{9\over AP}+ \ds{6\over AQ}=\ds{9\over AP}+ \ds{6\over \ds{3\over2}AP} =
\ds{9\over AP}+\ds{4\over AP} =\ds{13\over AP}$.
故に $AP = \ds{13\over6}$.
従って
$AQ = \ds{3\over2}\times \ds{13\over6} = \ds{13\over4}$.
さて (1) で求めた式により
$CF=\ds{EF\over2}\times\ds{CQ\over AQ}$
$= \ds{EF\over2}\times\ds{11\over 13}=\ds{11\over26}EF$.
従って
$4 = CE =EF-CF=EF -\ds{11\over26}EF = \ds{15\over26}EF$.
つまり $EF=\ds{4\times26\over15}$.
よって
$CF=EF-EC = \ds{4\times26\over15} - 4 = \ds{4\times26-4\times15\over15}$
$=\ds{4\times11\over15}=\ds{44\over15}$.
(3) (1) の議論より
$\ds{BP\over AP} +\ds{CQ\over AQ} =2\times\ds{ED\over DA} =10$ となれば良い。
$\ds{ED\over DA} =
5$
より
$AD = 5AD =\ds{1\over6}AE$.
$AG = \ds{2\over3}AE$.
$DG = AG-AD=\ds{1\over2}AE$
よって $\ds{AD\over DG} = \ds{\ \ds{1\over6}\ \over\ds{1\over2}} =\ds{2\over6}=\ds{1\over3}$.
結構難しい。
(1) の最後の所が出来ないと, あと全滅になってしまう。
これは高校で図形の問題をやらせないようにしたいという文部科学省の深謀遠慮であろう (皮肉である)。