.曲線 F(x, y) = 0 上の点 P(x, y) と, 原点との距離が限りなく大きくなるとき, 点 P から一定直線に下ろした垂線の長さが限りなく小さくなるような定直線が存在するとき, その直線をこの曲線の漸近線 asymptote という。
曲線 y = f(x) 上の動点を P(x, y) とし, 漸近線を g としよう
[1] g が y 軸に平行でない場合。
(1) g: Y = αX + β 即ち, Y - αX - β = 0 と置く。 P から g におろした垂線の足を H とすれば, Hesse の公式 (後で解説するが, これについて知らない人は, 気にしないでいい) から
.
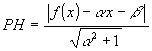g が漸近線であるとき, x→±∞ (のいずれか一方かもしれないが) PH→0 でなければならない。 もしも x→a で PH→0 だとすれば, それは g が y 軸に平行だから。
従って
であるから 
でなければならない (必要条件)。 β は定数なのだから limx→±∞(β/x)
= 0 である。 即ち
α = limx→±∞(f(x)/x) = limx→±∞(y/x).
又, これを用いて
β = limx→±∞(f(x) - αx) = limx→±∞(y - αx).
(2) 定義と, g が y 軸に平行でないことから, g は x→±∞ の時の接線の方程式の極限とも考えられる。 そこで P(x, y) 上の接線を
Y = f'(x)(X - x) + f(x) = f'(x)X + f(x) - f'(x)x
と置けば, 漸近線は
Y = limx→±∞(f'(x)X + f(x) - f'(x)x) = (limx→±∞f'(x))X + limx→±∞(f(x) - f'(x)x).
よって (1) での α = limx→±∞f'(x), β = limx→±∞(f(x) - f'(x)x). 勿論 de l'Hospital の定理によって limx→±∞(f(x)/x) = limx→±∞f'(x) である。
(3) m を定数として y = mx と曲線 φ(x, y) = 0 との交点を考え, m を -∞ から +∞ 間で変化させると, その交点が, 曲線上の全ての点を通るものと考えて良い。 そこで, 最初の曲線の式に, これを代入して
φ(x, mx) = 0.
これを x の方程式とみて, 解くと, この解は m に依存するので, x = F(m) と置く。 同様に y = G(m) と置いて, 解が (F(m), G(m)) であるとしよう。 k の値として ±∞ をも許容して m→k とする時, もしも F(m)→±∞, 又は G(m)→±∞ となるのならば, m = k の近くは曲線の対応する部分が無限に遠い所にあることを示している。 このような部分のことを無限分枝という。 曲線が無限分枝を持ち, この分枝に沿って点を動かして原点から離していく時, この無限分枝に幾らでも近付いていくような直線が存在するとすれば, それが漸近線である。 (1) でやったことを, この m に関して翻訳すればそれは
α = limm→k(G(m)/F(m))
β = limm→k(G(m) - αF(m))
である。 これは x についても y についても次数の高い曲線 φ(x, y) = 0 について漸近線を調べたり, 微分する時には便利な方法である。
[2] g が y 軸に平行な時。
これは g: x = a という場合である。 明らかに PH = |x - a| であるから, OP→∞ のとき, PH→0 ということだから即ち, x→a のとき f(x) = y → ±∞ なる場合。 或いは逆に述べて y → ±∞ なる時に x→a となる場合である。 これは大雑把に言って, y = f(x) という形で書いた時, f(x) の分母に x - a という形が出てくるときである (sin x や cos x 等の x = a のときに 0 となる函数が分母にでてくる場合も含む)。