解答 4

Proof of lemma.

f(x) = e^x - 1 - x - x²/2 と置くと f(0) = 0 で
f'(x) = e^x - 1 - x. f'(0) = 0 で
f''(x) = e^x - 1.

x ≧ 0, e > 1 より, f''(x) ≧ 0. 従って f'(x) は x ≧ 0 で単調増加。
従って f'(0) = 0 より x ≧ 0 で f'(x) ≧ 0. 従って f(x) は x ≧ 0 で単調増加。
よって f(0) = 0 より x ≧ 0 で f(x) ≧ 0.

∴ x ≧ 0 ⇒ e^x ≧ 1 + x + x²/2 で等号は x = 0 の時だけ。

戻る

[12] y = xe^-x.

e^x > 0 より, y 軸に平行な漸近線は存在しない。

lim_x→±∞(y/x) = lim_x→±∞(1/e^x).

x → +∞ の時:
lim_x→+∞(1/e^x) = 0.
ここで lemma から x > 0 の時
0 < y = x/e^x < x/(1 + x + x²/2) = 1/(1/x + 1 + x/2) → 0 as x → +∞.
∴ lim_x→+∞y = 0. よって y = 0 が漸近線。

x → -∞ の時:
t = -x と置けば t → +∞.
lim_x→-∞(1/e^x) = lim_x→-∞(e^-x) = lim_t→+∞(e^t) = +∞.
従ってこちら方向には漸近線は存在しない。

y' = e^-x - xe^-x = (1 - x)e^-x.
y'' = -e^-x - (1 - x)e^-x = (x - 2)e^-x.

x	…	1	…	2	…
y'	+	0	-
y''	-	-1/e	-	0	+
y		極大 e-1		変曲点 2/e2

戻る

[13] y = e^-xsin x.

e^x > 0, -1 ≦ sin x ≦ 1 より, y 軸に平行な漸近線は存在しない。

lim_x→±∞(y/x) = lim_x→±∞((sin x)/(xe^x).

x → +∞ の時:
|sin x| ≦ 1 より, (sin x)/x → 0, 1/e^x → 0. ∴y/x → 0.
lim_x→+∞y = lim_x→+∞((sin x)/e^x) = 0 (∵|sin x| ≦ 1, ex → + ∞).
従って y = 0 が漸近線。

x → -∞ の時: いつものように t = -x と置いて
lim_x→-∞(y/x) = lim_t→+∞((e^tsin(-t))/(-t)) = - lim_t→+∞((e^tsin t)/t).
e^t/t ≧ (1 + t + t²/2)/t = 1/t + 1 + t/2 → + ∞,
lim sup_t→+∞ sin t = 1, lim inf_t→+∞ sin t = -1 で不定符号だからこちら方向に漸近線はない。

y' = -e^-xsin x + e^-xcos x = -(√2)e^-xsin(x - π/4).
y'' = (√2)e^-xsin(x - π/4) - (√2)e^-xcos (x - π/4) = 2e^-xsin(x - π/2).

x	…	-3π/4	…	-π/2	…	π/4	…	π/2	…	5π/4	…
y'	-	0	+			0	-			0	+
y''	+			0	-			0	+
y		極小 -e3π/4/√2		変曲点		極大 eπ/4/√2		変曲点		極小 -e-5π/4/√2

これの graph を Microsoft Excel で描かせてみてはみたものの, y = e^-x の graph の減衰が激しく, 殆ど x 軸に張り付いているような図しか得られないため, 省略せざるを得ない。 これなどは, 手書きの方が気分が良く分かって良い (笑)。

どの位減衰が激しいかを示すために, sin x でいうと一周期分ほどを描いてみた。 上下の線は, 各々 y = e^x, y = e^-x である。

戻る

[14] y = e^x/(1 - e^x).

の時 y → ±∞ (複号同順) となるので, x = 0 (viz. y 軸) が漸近線。

lim_x→±∞(y/x) = lim_x→±∞(e^x/(x(1 - e^x))) = lim_x→±∞((1/x) / ((/e^x - 1)) = 0.

よって y = -1, y = 0 が漸近線。

y' = (d/dx)(e^x(1 - e^x)^-1) =e^x(1 - e^x)^-1 + e^x(1 - e^x)^-2e^x = (e^x(1 - e^x) + e^2x)(1 - e^x)^-2 = e^x(1 - e^x)^-2 = e^x/(1 - e^x)².
y'' = e^x(1 - e^x)^-2 + 2e^x(1 - e^x)^-3e^x = (e^x(1 - e^x) + 2e^2x) (1 - e^x)^-3 = e^x(1 + e^x)(1 - e^x)^-3 = e^x(1 + e^x)/(1 - e^x)³.

x	…	-0	+0	…
y'	+	×		+
y''	+	×		-
y		+∞	-∞

戻る

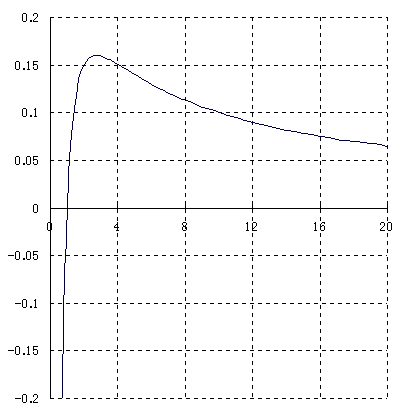
[15] y = x^-1log x.

定義域は対数函数の真数条件から x > 0.

x → +0 の時 t = log x と置くと, x = e^t だから, t → -∞ で,

y = e^-t・t → t/e^t → -∞.

従って x = 0 (viz. y 軸) は漸近線。

又, lim_x→+∞(y/x) = lim_x→+∞((log x)/x²) だが, 又 t = log x と置くと, x → +∞ の時, t → +∞ で [12] と同様に, lim_x→+∞(y/x) = lim_t→+∞(t/e^2t) = 0. 従って y = 0 (viz. x 軸) は漸近線。

y' = -x^-2 log x + x^-1・x^-1 = x^-2(1 - log x).
y'' = -2x^-3(1 - log x) + x^-2・(-x^-1) = x^-3(2log x - 3).

x	+0	…	e	…	e3/2	…
y'	+∞	+	0	-	-1/(2e3)	-
y''	-∞	-			0	+
y	-∞		極大 e-1		変曲点 3/(2e3/2)

x 切片は x = 1 である。

戻る