0
6(3-√3)e-(3-√3)
27e-3
6(9+5√3)e-(3+√3)
[22] y = x3e-x.
y' = 3x2e-x - x3e-x = x2e-x(3 - x).
y'' = 2xe-x(3 - x) - x2e-x(3 - x) -x2e-x.
= xe-x(6 - 2x - 3x + x2 - x) = xe-x(x2
- 6x + 6).
y'' = 0 とすると, x = 0, 3±√3.
y → ±∞ ならしめる x はない。
limx→±∞(y/x) = limx→±∞x2e-x = limx→±∞x2/ex.
さて x → +∞ の時, Lemma
と同様にして x > 0 ⇒ ex > 1 + x + x2/2 + x3/6
が証明できるので,
0 < y/x = x2/ex < x2/(1 + x +
x2/2 + x3/6) = 1/(1/x2 + 1/x + 1/2 + x/6) → 0.
∴limx→±∞(y/x) = 0.
同様に x > 0 ⇒ ex > 1 + x + x2/2 + x3/6
+ x4/24 から同様にして imx→±∞ y = 0
が分かるので, y = 0 (viz. x 軸) は漸近線。
x → -∞ の時, y/x → -∞ よりこちら方向には漸近線はない。
| x | … | 0 | … | 3-√3 | … | 3 | … | 3+√3 | … |
| y' | + | 0 | + | 6(2(√3)-3)e(√3)-3 | + | 0 | - | -6(3+2√3)e-3-√3 | - |
| y'' | - | 0 | + | 0 | - | 0 | + | ||
| y | 停留点 0 |
変曲点 6(3-√3)e-(3-√3) |
極大 27e-3 |
変曲点 6(9+5√3)e-(3+√3) |
|||||

[23] x + y2 = x2.
y = ±√(x2 - x). y 軸対称だから, y ≧ 0 のみを考える。 定義域は x ≦ 0, 1 ≦ x.
2yy' = 2x - 1. ∴y' = (2x - 1)/(2√(x2 - x)).
2(y')2 + 2yy'' = 2.
∴y'' = (1 - (y')2)/y = (1 - (4x2 - 4x + 1)/(4(x2
- x))) / √(x2 - x)
= -1/(4(x2 - x)√(x2 - x)).
y → ±∞ とする x はない。
limx→±∞(y/x) = limx→±∞ (±√(1 - 1/x)) = ±1.
limx→±∞(y - (±x)) = limx→±∞(√(x2 -
x) - (±x))
= limx→±∞((x2 - x - (±x2))/(√(x2
- x) ± x)) = limx→±∞±(-1/(√(1 - 1/x) + 1))
= -(±1/2), resp.
より, y = ±(x - 1/2) が漸近線。
| x | … | 0-0 | 1+0 | … |
| y' | - | -∞ | +∞ | + |
| y'' | - | × | × | - |
| y | 0 | 0 |

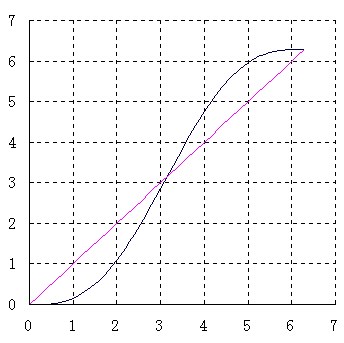
[24] y = x - sin x, 0 ≦ x ≦ 2π.
漸近線が存在しないのは明らか。
y' = 1 - cos x ≧ 0, y'' = sin x.
| x | +0 | … | π | … | 2π |
| y' | 0 | + | 2 | + | 0 |
| y'' | 0 | + | 0 | - | 0 |
| y | 0 | 変曲点 π |
2π |
[25] |y| = x - log|x|.
x 軸対称であるから, y ≧ 0 のみを考える。 定義域は x ≧ log|x| だから ex ≧ |x|.
y = x - log|x| であるから
y' = 1 - 1/x = (x - 1)/x.
y'' = 1/x2 > 0.
x → 0 の時 y → +∞ より, x = 0 が漸近線。
y/x = 1 - (log|x|)/x → 1 as x → +∞ が分かる (t = log x と置いて Lemma を用いよ)。 しかし y - x = - log |x| → -∞ as x → +∞ だからこちら方向には漸近線はない。
eα = -α と置いておく。
| x | α | … | -0 | +0 | … | 1 | … |
| y' | × | + | +∞ | -∞ | - | 0 | + |
| y'' | × | + | +∞ | +∞ | + | ||
| y | 0 | +∞ | +∞ | 極小 1 |
|||
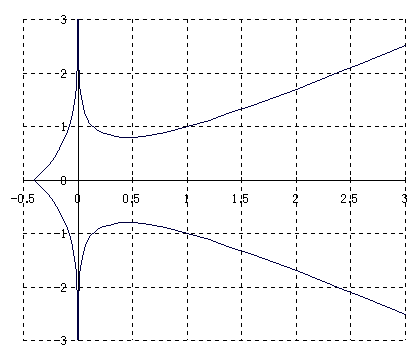
α ≒ 0.4 のようである。
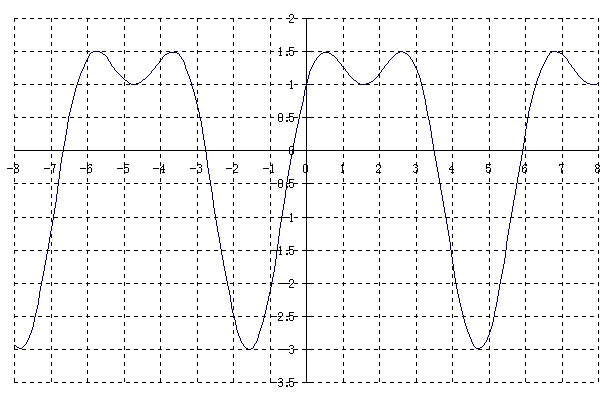
[26] y = cos 2x + 2 sin x.
y' = -2sin 2x + 2cos x = -4sin x cos x + 2 cos x = -2(2sin x - 1)cos x.
y'' = -4cos 2x - 2sin x = -4(1 - 2sin2x) - 2sin x
= 8sin2x - 2sin x - 4.
y'' = 0 とすると sin x = (1±√33)/8 でこれらはどちらも絶対値が 1 より小さいから, そのような x の値がある。
α = Sin-1((1+√33)/8), β = Sin-1((1-√33)/8) としよう。
y → ±∞ とする x はない。
y/x = (cos 2x)/x + 2(sin x)/x → 0 as x → ±∞. だが, y は x → ±∞ の時発散するから, 漸近線はない。
n ∈ Z とする。
| x | … | β+(2n-1)π | … | -π/2+2nπ | … | β+2nπ | … | π/6 | … | α+2nπ | … | π/2+2nπ | … | α+(2n+1)π | … | 5π/6+2nπ | … |
| y' | - | 0 | + | 0 | - | 0 | + | 0 | - | ||||||||
| y'' | - | 0 | + | 0 | - | 0 | + | 0 | - | ||||||||
| y | 変曲点 | 極小 -3 |
変曲点 | 極大 3/2 |
変曲点 | 極小 1 |
変曲点 | 極大 3/2 |
|||||||||