逆三角函数のところで述べたように, 一般に, 函数 y = f(x) に関し, ある函数 y = g(x) が存在して (定義域内の) どのような x に関しても f(g(x)) = x, g(f(x)) = x が成り立つとき, f と g とは互いに他の逆函数というのでした。 そこでは述べませんでしたが, f の逆函数を f-1 と書きます。これは f(f-1(x)) = f-1(f(x)） = x ですので, 丁度逆数を掛けるのと同じだ, という感覚から来ているらしいです。
さて y = f(x) という式の両辺を共に f-1 に入れると f-1(y) = f-1(f(x)) となりますが, この右辺は定義により x になりますので, 結局
f-1(y) = x
となるわけです。 このように見ると, 独立変数は y ですから, 両辺を y で微分しますと Leibniz の記号を用いれば
となります。 さて, 右辺がこの逆函数の微分だったわけですが --- ここから大分いいかげんな話になるが --- dx/dy というのは分数ですが, 当然, dy/dx の逆数です。そして dy/dx = f'(x) ですから
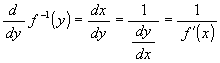
となるわけです。 この辺のお話をちゃんとするのは非常に難しい...。 [脚注 1]
いいかげんな話ついでに, 合成函数の微分について述べておきましょう。
y = f(x), z = g(y) であったとしましょう。つまり
です。 このとき, 代入して z = g(f(x)) となりますが,
このとき, x から z への対応を新たな函数と考えて, f と g の合成函数
composition といいます。記号で普通は 
と書くのですが, ここではとりあえず g○f
と書くことにします --- ○ がでかいけど,
ここしか出て来ないので我慢してください (笑)。
Leibniz の記号を用いますと y' = f'(x) = dy/dx, z' = g'(y) = dz/dy ですね ?
そこで dz/dx = d(g○f)/dx は次のように結果として約分される分数として考えることにします。
これを, 鎖の法則 chain law といいます --- 日本語訳は一定しない。 私の場合省略して鎖則等と言ったりする。 この辺を正しいお話にするのは難しいので, とりあえず分数だから当たり前と思ってください。 函数 f と g を用いて書けば
(g(f(x))' = f'(x)g'(f(x)).
標語的に言えば, 合成函数の微分は内側 (f) の微分と外側 (g) の微分を掛ける, ということになる。
一寸だけ意味を書きますと, スケール変換のところで述べたように, z = g(y) のところに, y = f(x) を代入しますと, x 軸方向に --- しかも x 毎に異なった --- スケール変換を受ける。 スケール変換は, 接線と同じ程度で効いて来る。 接線の傾きが y = f(x) の場合, f'(x) であったのだから, その分 scale factor として f'(x) がかかってくるのだと思ってよい。 実際, y = f(x) = ax + b, a ≠ 0 の場合は, スケール変換で述べたのとまったく同じ式になっている。 [脚注 2]
因みにこれを先に考えると, 上記の逆函数の微分も y = f(x) と f-1(y) = x, それから f-1(f(x)） = x の両辺を微分することによって
ですから, 前のように, dx/dy = 1/(dy/dx) という公式を得るわけです。
更に, この公式を用いると実は, 商の微分公式そのものが不必要であることが分かります。 というのは y = 1/g(x) = g(x)-1 と指数で書き換えることが出来るので,
y' = (1/g(x))' = (g(x)-1)' = g'(x)(-g(x)-2) = -g'(x)/g(x)2.
即ち前と同じ公式になるというわけである。
授業でやったら, この辺の話はとっても難しいらしい。 っていうか実際に微分できない。 計算は慣れなので, 頑張って練習するしかない。 頑張ろう !
脚注:
(1) dx/dy = 1/f'(x) で, f'(x) = 0 だったら ? と気付いた君 ! 君は鋭い !!
実はこの場合は |dx/dy| = ∞ となる --- | | は絶対値。 このことはつまり接線が y 縦軸に平行であるということを示しているのである。
(2) つまり極限 (limh→0) をとる前の Δy/Δx の誤差 o(h) は h → 0 で完全に 0 になるので, Δy/Δx = f'(x) + o(h) と誤差付きで書ける。 つまり Δy = f'(x)Δx + o(h)Δx.
だから f'(x) が scale factor になるわけである。