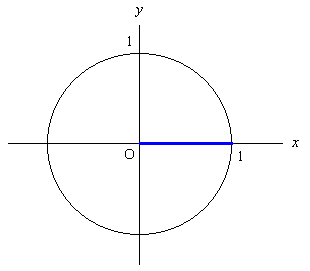
[0 rad]
0 rad の時は, 直角三角形を上手く作れないので, この場合には x = r cos θ, y = r sin θ の方を用いる。

動径の長さ r はどうでもいいから (笑) とりあえず 1 として x = cos 0, y = sin 0 として良い。 一般角として, x 軸の正の部分から 0 rad を取ると, 結局 x 軸の正の部分に重なっているので, 動径の先端は (1, 0) という座標の所にいる。 即ち cos 0 = 1, sin 0 = 0. tan 0 = sin 0/cos 0 = 0/1 = 0.
この説明は簡単で良いのだが, 不評だから (笑), 別の説明もしておく。 0 rad だと, 直角三角形は作られないが, 無理やり, 直角三角形だと思う。 つまり図のような --- 一寸いいかげんな --- 直角三角形を作る。
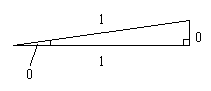
そうすると, 図にあるように, 底辺と斜辺は本当はぴったりくっついているのだから同じ長さ --- そこにあるように例えば 1 --- で, 高さは本当はぴったりくっついているのだから 0 である。 あとは cos 0 = 1/1 = 1, sin 0 = 0/1, tan である。
[π/6 rad]
π/6 rad = 30 度である。 一つの角が 30 度の直角三角形は, もう一つの直角でない角は 90 - 30 = 60 度である。 この 30, 60, 90 度の直角三角形は, 三角定規の一方であることに着目されたい。
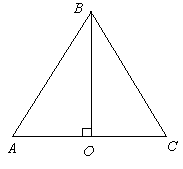
直角三角定規 AOB を図のように BO で折り返して, △ ABC を作る。 すると, ∠BAO = ∠BCO = 60 度だから, これは正三角形である。従って OA = 1 とすると, AB = BC = AC = AO + CO = 2AO = 2 である。 又, 三平方の定理から BO2 = AB2 - AO2 = 22 - 1 = 4 - 1 = 3. だから BO = √3.
よって
図から sin π/6 = 1/2, cos π/6 = (√3)/2, tan π/6 = 1/(√3).
[π/4 rad]
π/4 rad = 45 度である。 一つの角が 45 度の直角三角形は, もう一つの鋭角の大きさは 90 - 45 = 45 度なので, これは二等辺三角形。 斜辺の長さは, 三平方の定理から √(12 + 12) = √2.
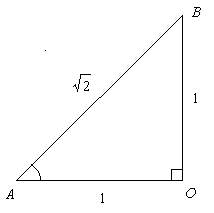
従って sin π/4 = 1/√2, cos π/4 = 1/√2, tan π/4 = 1/1 = 1.
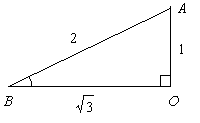
[π/3 rad]
π/3 rad = 60 度である。 作られる直角三角形は 30 度の時と同じである。
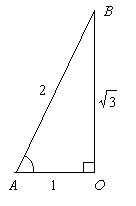
この図から sin π/3 = (√3)/2, cos π/3 = 1/2, tan π/3 = (√3)/1 = √3.
[π/2 rad]
π/2 rad = 90 度である。 これは 0 rad のときと同様に x = cos π/2, y = sin π/2 と考えて, 一般角として, x 軸の正の部分から反時計回りに π/2 rad を取ると, 結局 y 軸の正の部分に重なっているので, 動径の先端は (0, 1) という座標の所にいる。 即ち cos π/2 = x = 0, sin π/2 = y = 1. tan であるが, tan θ = sin θ/cos θ だから, 無理矢理やると, tan π/2 = 1/0 となってしまうが, 分母を 0 にしてはいけないので, これは定義しない。
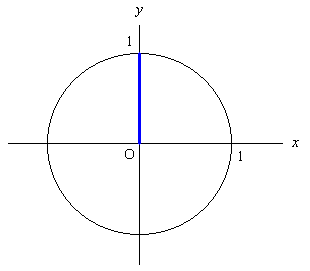
この説明も評判が悪いんで (笑) 別の説明をしておく。 これも無理矢理直角三角形を作る。
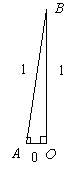
実は AB と BO はぴったりくっついているということに注意しておくと, AB = BO = 1, AO = 0 である。 だから sin π/2 = 1/1 = 1, cos π/2 = 0/1 である。
[2π/3 rad]
2π/3 = 180×2/3 度 = 120 度 である。 180 - 120 = 60 度だから, 一般角として, x 軸の正の部分から, 反時計回りに 120 度をとると, これは x 軸の負の部分から, 時計回りに 60 度をとったのと同じことになる。 (以後この説明を省く)
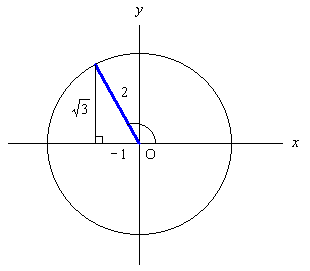
そこでこの動径と円との交点から x 軸に垂線を下ろすと, それは三辺の比が 1 : 2 : √3 の直角三角形になる。 ところで, 動径が第一象限以外の場合には, 辺の長さというものに関し, 符号を考えなければいけないのであった。 動径は (半径だから) 常に +, 縦線は y 軸と一緒であるから, この場合 +, 横線が x 軸と一緒なので, この場合 - である。 (以後この説明も省く)
従って sin 2π/3 = (√3)/2, cos 2π/3 = (-1)/2 = -1/2, tan 2π/3 = (√3)/(-1) = -√3.
[3π/4 rad]
3π/4 = 180 度× 3/4 = 135 度。 180 度 - 135 度 = 45 度。
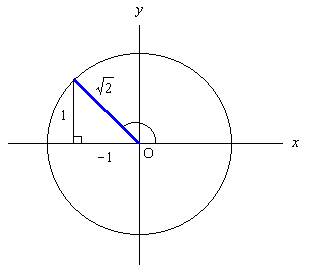
図のようになるので, sin 3π/4 = 1/√2, cos 3π/4 = -1/√2, tan 3π/4 = 1/(-1) = -1.
[5π/6 rad]
5π/6 = 180 度 × 5/6 = 150 度。 180 - 150 = 30 度。
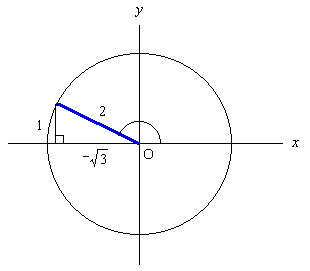
図のようになるので, sin 5π/6 = 1/2, cos 5π/6 = -(√3)/2, tan 5π/6 = 1/(-√3) = -1/√3.
[π rad]
π rad = 180 度である。 この場合も 0 rad のときと同様に x = cos π, y = sin π と考えて, 一般角として, x 軸の正の部分から反時計回りに π rad を取ると, 結局 y 軸の正の部分に重なっているので, 動径の先端は (-1, 0) という座標の所にいる。 即ち cos π = x = -1, sin π = y = 0, tan π = sin π/cos π = 0/1 = 0 である。
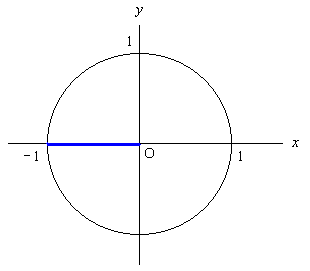
勿論, これも前と同様に, 無理矢理, 角度をつけて次の図のようにしても同じ結果を得る。 動径は + だが横方向の線は - であることに注意しよう。
あと半周だ ! 頑張ろう !