kaneda naoki 氏から, shell method とは何か ? という質問をいただいた (on Monday 11th March, 2002)。 不勉強にして知らなかったので, USA の Yahoo ! で "shell method volume" で検索したところ, これもどうやら回転体の体積を求めるのに用いられる公式であることが分かった。 英語の site ではここが良いように思われる。
あとで同僚に聞いたところこれは日本では 「バウムクーヘン積分」 或いは 「バームクーヘン積分」 という形で良く知られているらしい。 勿論お菓子の Baumkuchen から来ているのである。
やり方はこうである。
定理
函数 y = f(x) は閉区間 [a, b] (但し a ≧ 0) で可積分且つ f(x) ≧ 0 とする。 函数 y = f(x) の graph と, 直線 y = 0 (viz. x 軸), x = a, x = b で囲まれた部分の体積 V は
V = 2π∫ab x f(x) dx
である。
図は先程の英語の site が良く描けているので, 英語が読める人はそこを見た方が良く分かると思う。 問題しか出ていなかったがこういう文献もあった (ここに出ている傘型分割というのが何を意味しているのか不明だった)。
私の感じでは Baumkuchen というよりは桂剥き (かつらむき) といった感じなのだが, 要するに, 回転体の体積を求めるのに, 回転軸に直角方向に分割していく (輪切りの) 通常の方法を取らずに, 回転軸からの距離が等しい円筒に分割していく方法である。 定理を見れば分かるように, 普通の輪切りの方法だと x = f-1(x) を求めなければいけないが, この方法だとそのまま出来るので便利である。
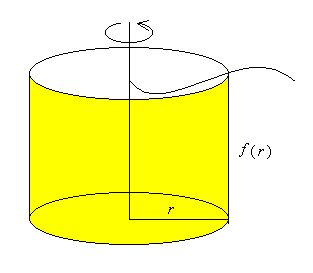
要するに, 回転軸からの距離が r の点は高さが f(r) の円筒 (の側面) を作っている。 この円筒の面積は 2πr f(r)である。 従ってこれに厚み dr を掛けて積分すればよいというわけである。

勿論 x 軸中心の回転であったら函数の方は x = g(y) の形をしている必要があって V = 2π∫ab yg(y)dy となるわけである。
尚, USA でこの方法を何故 shell method
というかについてはまったく不明である。 最初に掲げた
kaneda naoki 氏からの mail には
V = ∫ab 2π(shell radius)(shell height) dx
の形で出ていたので, アメリカ人達は,
二枚貝か何かの生長曲線を連想するのかもしれないなと思った次第である。