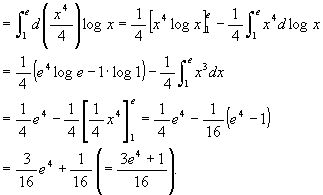
<review> 先ず公式を復習しておこう:
∫abf(x)g'(x) dx = [f(x)g(x)]ab - ∫abf'(x)g(x) dx.
注意しなければならないのは, 右辺の第一項に, 上端と下端がついていることである。 これを忘れる人がたまにいる。
[1] ∫1e log x dx
与式 = [x log x]1e - ∫1e x
dlog x
= e log x - 1 log 1 - ∫1e x・dx/x
= e - ∫1e dx = e - (e - 1) = 1.
[2] ∫1e x3 log x dx
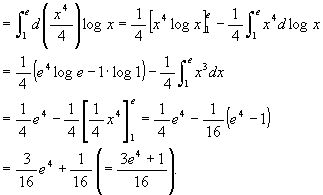
[3] ∫0e log (|x - 1| + 1) dx
与式 = ∫01 + ∫1e log (|x -
1| + 1) dx …… 積分区間の分割
= ∫01 log(-x + 2) dx + ∫1e logx
dx …… 絶対値の定義に従って計算
ここでは前の部分が 0 ≦ x ≦ 1 だから x - 1 ≦ 0 なので |x - 1| = -(x - 1) = -x + 1 になる, 後半は 1 ≦ x ≦ e だから同様にして |x - 1| = x - 1.
ここから部分積分に入るが, 後ろは [1] に従って 1 に等しい。 問題は前半だが, log の中が (-x + 2) だから, dx が f'(x) だと思わずに, -d(-x + 2) = dx を用いた方が計算が楽になる。 つまり
与式 = -∫01 d(-x + 2) log(-x + 2) + 1
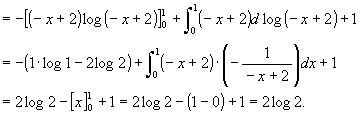
[4] ∫αβ(x - α)(x - β)dx = -(β - α)3/6.
最初に部分積分を用いない方法で示す。 積分区間の下端が α なので, x - α を作る。
左辺 = ∫αβ(x - α)((x - α) - (β- α))dx
= ∫αβ((x - α)2 - (β- α)(x - α)) dx
= [(x - α)3/3 - (β- α)(x - α)2/2]αβ
= (β - α)3/3 - (β - α)3/2 = 右辺。
次に, 部分積分で示す。
左辺 = ∫αβd((x - α)2/2)(x - β)
= (1/2)[(x - α)2(x - β)]αβ - (1/2)∫αβ(x
- α)2dx
=(1/2)(0 - 0) - (1/2)(1/3)[(x - α)3]αβ
=右辺。
[5] ∫-11(x + 1)3(x - 1)dx
これは次数の高い方が微分されていると思って
与式 = ∫-11d((x + 1)4/4)(x - 1)
=[(1/4)(x + 1)4(x - 1)]-11 - (1/4)∫-11(x
+ 1)4dx
= (0 - 0) - (1/4)(1/5)[(x + 1)5]-11
= -(1/20)・25 = -(1/5)・23 = -8/5.
この, [4], [5] を見ると, 次のような計算をしてみたくなるであろう。
[6] m, n を自然数とするとき,
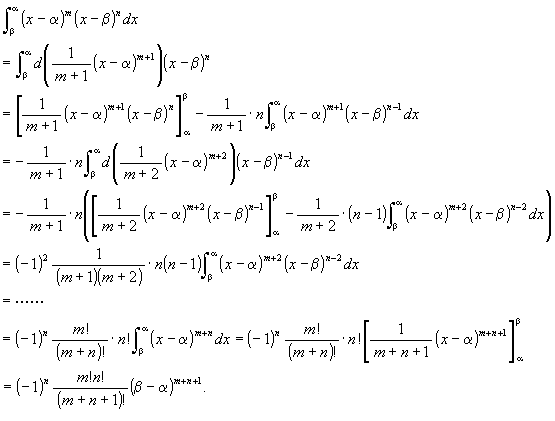
[7] ∫0πx sin x dx
= ∫0πx d(-cos x)
= [-x cos x]0π + ∫0πcos x dx
= (-π cos π) - (-0・cos 0) + [sin x]0π
= -π・0 + sin π - sin 0 = π.
[8] 同様にして ∫0πx cos x dx = -2.
[9] 更に同様に ∫0π/2x sin x dx = 1.
[10] ∫0πe2x sin x dx
= ∫0πd(e2x/2)sin x
=[(e2xsin x)/2]0π - (1/2)∫0πe2x
cos x dx
= -(1/2)∫0πd(e2x/2)cos x
= -(1/2)([(e2xcos x)/2]0π +(1/2)∫0πe2x
sin x dx)
= -(1/2)(e2πcos π)/2 - (cos 0)/2) - (1/4)∫0πe2x
sin x dx
= -(1/2)(e2π・(-1)/2 - 1/2) - (1/4)∫0πe2x
sin x dx
= (e2π + 1)/4 - (1/4)∫0πe2x sin
x dx.
即ち
∫0πe2x sin x dx = (e2π + 1)/4 - (1/4)∫0πe2x sin x dx.
ここで右辺第二項を左辺に移項して
(5/4)∫0πe2x sin x dx = (e2π + 1)/4
故に与式 = = (e2π + 1)/5.
実は, この場合は sin x = d(-cos x) を用いた方が, 分数が出てこなくて易しい。 (詳細省略)
[11] n を自然数とするとき:
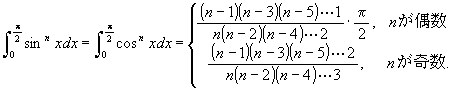
通常 n が偶数のとき, n(n - 2)(n - 4)・…・4・2 = 2n/2((n/2) !), n が奇数のとき n(n - 2)(n - 4)・…・3・1 = (n !)/(2(n-1)/2(((n-1)/2) !)) のことを n !! と書くので, この公式は通常次のように簡単に書かれている。
∫0π/2 sinn x dx = ((n - 1) !!/ n !!)(π/2), n が偶数, = ((n - 1) !!/ n !!), n が奇数。
さて, 先ず ∫0π/2 sinn x dx = ∫0π/2 cosn x dx を示そう。 (graph から明らかだが)
t = π/2 - x と置くと x = 0 ⇒ t = π/2, x = π/2 ⇒ t = 0 であり, dt = -dx 即ち dx = -dt だから
∫0π/2 sinn x dx = ∫π/20 sinn (π/2 - t) (-dt) = -∫π/20 cosn t dt = ∫0π/2 cosn x dx.
次に最後の等号を示そう。
∫0π/2 sinn x dx = ∫0π/2 sinn-1 x
sin x dx
= ∫0π/2 sinn-1 x d(-cos x)
=[-sinn-1 x cos x]0π/2 + ∫0π/2
d(sinn-1 x) cos x
= 0 + ∫0π/2 (n - 1)sinn-2 x cos2
x dx
= (n - 1)∫0π/2 sinn-2 x (1 - sin2
x) dx
= (n - 1) ∫0π/2 sinn-2 x dx - (n - 1)∫0π/2 sinn x dx.
最後の項を移項して
n∫0π/2 sinn x dx = (n - 1) ∫0π/2 sinn-2 x dx.
n で割ると
∫0π/2 sinn x dx = ((n - 1)/n) ∫0π/2 sinn-2 x dx.
要するにこれは, sin の指数が二つずつ減っていき, 前についている分数は, その指数 + 1 になっているので,
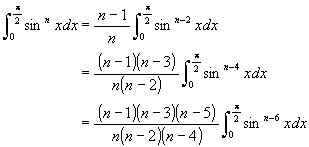
の様になっていく。 問題は何処まで指数が減らせるかであるが, n が偶数のときは
∫0π/2 sin2 x dx = ∫0π/2
(1 - cos2 x) dx = ∫0π/2 dx - ∫0π/2
cos2 x dx
= π/2 - ∫0π/2 sin2 x dx
だからいつものように移項して
∫0π/2 sin2 x dx = (1/2)(π/2)
まで下げられる。
奇数の場合には, 例えば n = 3 で考えると
∫0π/2 sin3 x dx = (2/3)∫0π/2 sin x dx
= (2/3)[- cos x]0π/2
= (2/3)(-cos(π/2) + cos 0) = 2/3.
よって上記の結果を得る。
この結果を使うと, 結構計算が楽になることがある。 以下幾つかその練習。
[12] ∫0π/2 sin4 x dx = ((3・1)/(4・2))(π/2) = 3π/16.
[13] ∫0π/2 cos5 x dx = (4・2)/(5・3) = 8/15.
[14] ∫0π sin3 x dx …
積分区間に注意
= ∫0π/2 + ∫π/2π sin3 x dx
… y = sin x のgraph が直線 x = π/2
に関し対称であることを用いる。
= 2∫0π/2 sin3 x dx … graph の対称性
(後ろの方を t = x + π/2 と置換しても出る)。
= 2・(2/3) = 4/3.
[15] ∫0π cos4 2x dx
これは先ず t = 2x と置く。
与式 = ∫02π cos4 t dt/2
= (1/2)(∫0π/2
+∫π/2π + ∫π3π/2 ∫3π/22π cos4
t dt) … π/2 の長さの区間に分割。
= (1/2)・4∫0π/2
cos4 t dt … 偶数乗なので,
符号の問題は起こらない。
= (1/2)・4・((3・1)/(4・2))・π/2 = 3π/8.