指数・対数函数の極限

[review]

1. lim_x→±∞ (1 + 1/x)^x = e.
2. lim_x→0 (1 + x)^1/x = e.
3. lim_x→+∞ (1 + x)^1/x = 1.
4. lim_x→+0 (1 + 1/x)^x = 1.

基本的には次のような感じになっている。

lim (f(x))^g(x) について

1. f(x) = 1 + t 又は 1 + 1/t と置く。
2. f(x) → 1, g(x) → ±∞ は e が出てくる。
   f(x) → ±∞, g(x) → 0 は 「1 が出て来る」。

2. の後半に関しては, 正確には (超越数である e ではなくて) 普通の数が出て来ると言うべきか。

例: 次の各々の極限を求めよ。 a,b は定数で ab ≠ 0 である。 尚, 必要ならば e > 1 を用いよ。

(1) lim_h→0 (e^h - 1)/h.

(2) lim_h→0 (e^ah - 1)/(bh).

(3) lim_h→0 (log(1 + h))/h.

(4) lim_x→0 (1 - sin x)^1/x.

(5) lim_h→0 (a^h - 1)/h (ここでは a > 0)

(6) lim_x→∞ ((a^1/x + b^2/x)/2)^2x. (この問題では a > 0, b > 0 の定数)

(7) lim_x→∞ x(log(x + 2) - log x).

解答:

(1) (もう既にこれは y = e^x の x = 0 に於ける微分係数の定義だということはお分かりであろう。) h > 0  とすると e > 1 より e^h > 1, 又, h < 0 とすると e^h < 1. 従って e^h = 1 + 1/t と置くと, h → ±0 の時 t → ±∞. 又 h = log(1 + 1/t).

従って lim_h→0 (e^h - 1)/h = lim_t→±∞ 1/(t log(1 + 1/t)) = 1/lim_t→±∞ (log(1 + 1/t)^t) = 1/log (lim_t→±∞ (1 + 1/t)^t) = 1/ log e = 1.

尚, これは今後公式として用いて良い。

(2) t = ah と置くと h = t/a, t → 0 (as h → 0). 従って (1) によって

lim_h→0 (e^ah - 1)/(bh) = lim_t→0 (e^t - 1)/(bt/a) = (a/b)lim_t→0 (e^t - 1)/t = a/b.

(3) t = 1/h と置くと, h → ±0 の時 t → ±∞. lim_h→0 (log(1 + h))/h = lim_t→±∞ (t log(1 + 1/t)) = lim_t→±∞ log(1 + 1/t)^t = log lim_t→±∞ (1 + 1/t)^t = log e = 1.

(4) t = -sin x と置くと, x → 0 の時 t → 0 で

lim_x→0 (1 - sin x)^1/x = lim_t→0 (1 + t)^(1/t)(t/x) = e^-1 = 1/e.

ここで t/x = (- sin x)/x → -1 (as x → 0) を用いた。

(5) a = 1 の時は明らかに与式 = 0. それ以外の時, a^h = 1 + h と置くと, h → 0 の時 t → 0 で

lim_h→0 (a^h - 1)/h = lim_t→0 t/log_a(1 + t) = lim_t→0 1/((1/t)log_a(1 + t)) = lim_t→0 1/(log_a(1 + t)^1/t) = 1/log_alim_t→0 (1 + t)^1/t = 1/log_a e = log a.

この結果は a = 1 をも含んでいる。

(6) (a^1/x + b^2/x)/2 = 1 + 1/t と置く。 このとき t = 1/((a^1/x + b^2/x)/2 - 1) = 2/(a^1/x + b^2/x - 2) であるから x → ∞ の時 |t| → ∞. 故に lim_x→∞ ((a^1/x + b^2/x)/2)^2x = lim|t|→∞ (1 + 1/t)^t(2x/t).

又 x = 1/u と置くと, x → ∞ の時 u → +0 で (5) より

lim_x→∞ 2x/t = lim_x→∞ x(a^1/x + b^2/x - 2) = lim_u→+0 (a^u - 1 + b^2u - 1)/u = lim_u→+0 ((a^u - 1)/u + 2(b^2u - 1)/(2u)) = log a + 2 log b = log(ab²).

従って与式 = e^{log a + 2 log b} = ab².

(7) 対数法則により lim_x→∞ x(log(x + 2) - log x) = lim_x→∞ x log((x + 2)/x) = lim_x→∞ x log(1 + 2/x) = lim_x→∞ log(1 + 2/x)^x = 2lim_x→∞ log(1 + 1/(x/2))^x/2 = 2 log e = 2.

練習: 次の各々の極限を求めよ。 a,b は定数で ab ≠ 0 である。

(1) lim_h→0 (1 - e^2h)/h.

(2)

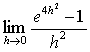
(3) lim_h→0 (e^h - 2)/h.

(4) lim_h→0 h/(e^2h - 1).

(5) lim_h→0 (log(1 + ah))/(bh).

(6) lim_h→0 (log(1 - h))/h.

(7) lim_h→0 (log(1 + 3h))/(2h).

(8) lim_h→0 (log(2 + h))/h.

(9) lim_h→0 (-h/log(1 + 2h))

(10) lim_x→0 (sin x)/log (1 + x).

(11)

略解: (1) -2, (2) 4, (3) -(±∞) (as h → ±0, 複号同順), (4) 1/2. (5) a/b, (6) -1, (7)  3/2, (8) ±∞ (as h → ±0, 複号同順), (9) -1/2, (10) 1 (分子分母を x で割れ), (11) √e (= e^1/2) (t = 1 - cos x と置け).

問題:

1. 函数 f(x) は a > 1, x > 1 に対し f(x) = lim_h→0 ((log_a x)h - 1)/h で定義されている。 このとき f(x²) - f(x) を求めよ。
2. a_n = ((n + 1)/(n + 2))ⁿ(n + 1 + sin n)/(n + 2) であるとき lim_n→∞ a_n を求めよ。

解答:

1. t = log_ax と置くと f(x) = limh→0 (th - 1)/h = log t (by 例 (5)) 従って f(x) = log(log_ax). 故に f(x²) - f(x) = log(log_ax²) - log(log_ax) = log(2log_ax) - log(log_ax) = log((2log_ax)/(log_ax)) = log 2.

2. a_n = (1 - 1/(n + 2))ⁿ((1 + 1/n + (sin n)/n)/(1 + 2/n)
= (1 + 1/(-(n + 2)))^{-(n+2)(-n/(n+2))}×((1 + 1/n + (sin n)/n)/(1 + 2/n)
= (1 + 1/(-(n + 2)))^{-(n+2)(-1/(1+2/n))}×((1 + 1/n + (sin n)/n)/(1 + 2/n)
→e^{-1/(1 + 0)}×(1 + 0 + 1)/(1 + 0) = e^-1×2/1 = 2/e (as n → ∞).

次へ
函数の極限の目次へ