今まで考えてきた数列の極限は, 自然数 n からの対応 n → an に関し, n → ∞ の時の数列 an の状況を考えるということだった。
函数は無限に多い数 x から f(x) という数を対応させる規則なので, n → ∞ というようにいつも同じところでの極限というものを考えるわけにはいかない。 函数の極限を考えるとは: 函数 y = f(x) に於て, x が a に限りなく近付くとき, f(x) が α に限りなく近付いていくとき, この α を x が a に近付くときの f(x) の極限 limit というのである。
書き方は数列の時と同様で
或いは
x → a のとき f(x) → α,
f(x) → α (as x → a),
,
等と書く。 数列の時同様に, この site では
limx→a f(x) = α
のように書いてあることが多い。
函数の極限については, 数列の極限と n→∞ でない点を除けばほぼ同じである。
数列の極限で書いておいた ε-δ 論法についても書いておこう。 数列の場合 limn→∞ an = α とは ∀ε > 0∃N∈N(n > N ⇒ |an - α| < ε) の略であった。 函数ではこうである。
limx→a f(x) = α ⇔ ∀ε > 0∃δ > 0(0 < |x - a| < δ ⇒ |f(x) - α| < ε)
つまり, どのように誤差 ε を小さく見積もっても, x と a の距離を δ より小さく押さえれば, f(x) と α は最初に定めた誤差 ε よりも小さくできることが保証されるときに, 「x → a の時に f(x) → α だ」 というということである。
言ってみれば, x を a の近く (数学用語で δ-近傍 δ-neighbourhood, δ-neighborhood という。 略して δ-nbd 等と書く。 正確には δ-nbd から a そのものを除いたものである) に制限してやると, f(x) の方もそれにつられて α の近く (ε-nbd) に凝集してくるというイメージである。
実際問題として, 極限値を計算する場合には, 本質的に代入する以上の計算をすることは稀ではあるが,
対数函数の微分の時のように未知の函数の極限
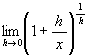を計算しようといったときに太刀打ちできなくなってしまう。 このような場合どうするのか ? それは a という実数がどういう風に決まっているか (実数の公理)
と関わりを持っているのだが次のように, xn → a となるどのような数列に対しても f(xn) が (数列として)
一定の極限値を持つことと解釈される。 こうして
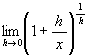は h → 0 となるような数列
(例えば x/n) で置き換えて実験してみることが意味のあることとなるわけである。
[定理]
limx→a f(x) = α
⇔
∀数列 {xn} (∀n(xn ≠ a) & limn→∞xn = a ⇒ limn→∞f(xn) = α)
正確には a = ±∞ 等も含めて言う。 証明は a も α も有限な場合だけ書いておく。
証明:
limx→a f(x) = α ⇔ ∀ε > 0∃δ > 0(0 < |x - a| < δ ⇒ |f(x) - α| < ε) を仮定する。 ここで数列 {xn} が ∀n(xn ≠ a) & limn→∞xn = a を満たしているとすれば, 数列の極限の定義から同じ δ > 0 に対し∃N∈N(n > N ⇒ 0 < |xn - a| < δ) であるから n > N ⇒ |f(xn) - α| < ε であるので, limn→∞f(xn) = α が成り立っている。
逆に ∀数列 {xn} (∀n(xn ≠ a) & limn→∞xn = a ⇒ limn→∞f(xn) = α) が成立しているとしよう。 背理法を用いて証明するために, 結論を否定して ∃ε > 0∀δ > 0(0 < |x - a| < δ & |f(x) - α| ≧ ε) (つまりある限界の誤差 ε が存在して, x を a のどんなに近くにとって来ても, f(x) と α の誤差はその ε 以上になってしまう) と仮定しよう。 ところがもしそうだとすれば, (例えば) 0 < |xn - a| < 10-n の時に |f(xn) - α| ≧ ε となる数列 {xn} があることになって矛盾である。□
この定理を準備すると, 数列と同様, Cauchy の判定法が成立することが証明できる。
[定理]
有限な limx→a f(x) が存在する
⇔
∀ε > 0∃δ > 0(0 < |x' - a| < δ & 0 < |x" - a| < δ ⇒ |f(x') - f(x")| < ε)
証明:
limx→a f(x) = α ⇔ ∀ε > 0∃δ > 0(0 < |x - a| < δ ⇒ |f(x) - α| < ε/2) だから, 三角不等式を用いて
0 < |x' - a| < δ & 0 < |x" - a| < δ
⇒ |f(x') - f(x")| = |f(x') - α + α - f(x")| ≦ |f(x') - α| + |α - f(x")| =
|f(x') - α| + |f(x") - α| < ε/2 + ε/2 = ε.
さて逆に, ∀ε > 0∃δ > 0(0 < |x' - a| < δ & 0 < |x" - a| < δ ⇒ |f(x') - f(x")| < ε) としよう。このとき, ∀数列 {xn} (∀n(xn ≠ a) & limn→∞xn = a) に対して ∃N∈N(n > N ⇒ 0 < |xn - a| < δ) であるから仮定によって n, m > N ⇒ |f(xn) - f(xm)| < ε. 従って, 数列に関する Cauchy の判定法によって, {f(xn)} は有限の極限値を持つ。 これが数列 {xn} によらず, 一定の値であることを示そう。 別の数列; {x'n} (∀n(x'n ≠ a) & limn→∞x'n = a) をとり, x"n = (((-1)n + 1)xn/2 + ((-1)n-1 + 1)x'(n+1)/2)/2 を考えると, 奇数番目では {x'n} に, 偶数番目では {xn} に一致するから, これは条件 ∀n(x"n ≠ a) & limn→∞x"n = a) を満たしており, 従って, limn→∞f(x"n) が存在しなくてはならない。 そして, 作り方から明らかに, それは limn→∞f(xn) とも limn→∞f(x'n) とも一致しなくてはならない。 だから上記の定理によって, 有限な limx→a f(x) が存在する。□