積分可能性

記号は前の page のものを踏襲する。

定理

函数 f(x) が可積であるための必要十分条件は

∀ε > 0 ∃Δ: 分割 (S_Δ - s_Δ < ε).

証明:

前の page で証明したように可積であるための条件は _∫_a^b f(x) dx = ˉ∫_a^b f(x) dx であった。 Darboux の定理により, このとき 0 ≦ _∫_a^b f(x) dx - s_Δ < ε/2, 0 ≦ S_Δ - ˉ∫_a^b f(x) dx < ε/2 と出来るから辺々加えれば 0 ≦ S_Δ - s_Δ < ε.

逆に S_Δ - s_Δ < ε となる分割 Δ が存在すれば, Riemann 過剰積分, 不足積分の (sup 及び inf による) 定義によって 0 ≦ ˉ∫_a^b f(x) dx - _∫_a^b f(x) dx ≦ S_Δ - s_Δ < ε だから _∫_a^b f(x) dx = ˉ∫_a^b f(x) dx とならねばならない。□

定義

函数 f(x) について区間 I 上で

osc_I f(x) = sup_I f(x) - inf_I f(x)

と定め, これを f(x) の I 上の振幅 oscillation (又は変動 variation)と呼ぶ。

以下では分割 Δ によって生じた各細区間 I_i の振幅を v_i = M_i - m_i で表す。 このとき

S_Δ - s_Δ = Σ_i=1ⁿ(M_i - m_i)δ_i = Σ_i=1ⁿ v_iδ_i

であることに注意されたい。

定理

函数 f(x) が区間 I で可積
⇔∀ε > 0 ∃δ > 0 ∃Δ: 分割 ().
Σ の意味は, 細区間 I_i の内, そこでの振幅 v_i が δ より大になるようなものだけをとってきて, その幅 δ_i の和をとるということである。

証明

f(x) が可積とすれば上記の定理によって分割 Δ が存在して S_Δ - s_Δ < δε と出来る。 すぐ上の注意により

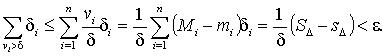
逆に を満たす分割 Δ が存在すると, Σ を次のように分割して評価すると

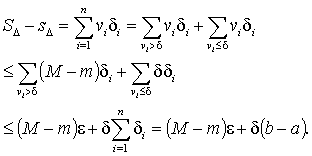
である。 この最後の部分では ε は任意, δ はある程度以下ならばよいので, 幾らでも小さくとることが出来る。 従って任意の ε' > 0 に対し S_Δ - s_Δ < ε' と出来るので, 可積である。□

可積でない函数の例: 所謂 Dirichlet の函数

f(x) = 1, x ∈ Q, f(x) = 0, ¬(x ∈ Q)

(有理数の時 1, そうでない (無理数の) 時 0) とする。 有理数も無理数も R で稠密だから, どのように区間を細分しようと常に m_i = 0, M_i = 1 なので v_i = 1. 従って f(x) はどんな有限閉区間をとっても可積にはならない。 実際 ˉ∫_a^b f(x) dx = b - a,  _∫_a^b f(x) dx = 0.

この函数は全ての点で不連続であるが, 不連続を持っても有界で且つ単調ならば可積である。 実際 f(x) が I で単調増加であるとすると M_i = f(x_i), m_i = f(x_i-1) であるから S_Δ = Σ_i=1ⁿ f(x_i)δ_i, s_Δ = Σ_i=1ⁿ f(x_i-1)δ_i なので S_Δ - s_Δ = Σ_i=1ⁿ (f(x_i) - f(x_i-1))δ_i < Σ_i=1ⁿ (f(x_i) - f(x_i-1))δ = (f(b) - f(a))δ だから。

しかし, 不連続点を持つ有界で単調な函数がどの位不連続点を持ち得るかはこの段階では分からない。

可積だが不連続点が稠密に存在する例を一つ挙げよう。 次の例は高木貞治による。 区間 [0, 1] に属する x の値を二進法に書き表して, それを十進法によって読むときの値を y = f(x) とする。 但し 2 の冪を分母とする有理数は有限二進数で表すものとする。 例えば f(1/2) = 0.1, f(1/4) = 0.01, f(3/4) = 0.11 (こういう風に注意したのは 1/2 は無限二進小数で表すと 0.011111...... であるからである)。

この函数は [0, 1] で有界で, 単調に増大するが p/2ⁿ が不連続点で, 稠密に分布されている 。 例えば f(1/2) = 0.1 であるが 1/2 は 0.01111... と無限二進小数で表すことも出来るので 0.1 = 1/10, 0.0111... = 1/90 である。 このことから考えて f(1/2 - 0) = 1/90, f(1/2) = 0.1, ここでの飛びは 8/90. 同様にして p/2ⁿ での飛びは (8/9)/10ⁿ である。 しかし有界で単調増加だから可積である。

定理

函数 f(x) が区間 I で可積ならば, 任意の [c, d] ⊂ I は f(x) の連続点を含む。 (従って連続点は I の中に稠密に存在する)

この定理からも Dirichlet の函数が可積でないことが分かる。

証明:

f(x) が可積であるから, ある分割が存在して, f(x) の振動が 1/2 より大きいような分割の細区間の長さの和は d - c よりも小さい。 従って, 区間 (c, d) は f(x) の振動が 1/2 以下であるような細区間 (c₁, d₁) を含む。 (必要ならば更に小さい区間で同じ論法を適用すればよいから) c < c₁ < d₁ < d, d₁ - c₁ < (1/2)(d - c) として良い。 以下帰納的に (c_k, d_k) を定義していき, (c_k-1, d_k-1) は f(x) の振動が 1/2^k 以下である部分区間 (c_k, d_k) を含み, 更に c_k-1 < c_k < d_k < d_k-1, d_k - c_k < (1/2)(d_k-1 - c_k-1) を満たすようにとっていく。 すると, Bachmann の縮小区間法の定理 (実数の公理の中にある) によって, この区間列は, I の内部に実数 α を定める。 この α に対し, 任意の ε > 0 とそれに対応するある δ > 0 をとれば osc_{|x - α|≦δ} f(x) < ε と出来る (そうなるように α が定まっている)。 従って α は f(x) の連続点である。□

定理

区間 I に有限個しか不連続点を持たない函数 f(x) はそこで可積。 特に I で連続な函数は可積。

証明

∀ε > 0 に対し, I の中に存在する f(x) の有限個の不連続点全体 {c₁, ..., c_n} を含む区間の和 ∪_i=1ⁿ (c_i, d_i) を (有限個だから) Σ_i=1ⁿ (d_i - c_i) < ε とすることが出来る。 但し, I の端点 a 又は b 自身が不連続点の時には [a, d₁), (c_n, b] のように, 端だけ半開区間とする。 必要ならば区間の幅を狭くして, 番号を付け直し d_k < c_k+1 となっているようにできる。

元の区間 I から上記の区間を除いた残りは有限個の閉区間である。 Heine の定理 (一様連続性) により, f(x) はその各々の閉区間で一様連続だから, 必要ならばその閉区間を更に細分して, それらの区間での振動を全て δ よりも小であるようにできる。 この分割に更に [c_i, d_i] を加えることによって I の分割が得られ, それに対しては今の作り方より (ここだけ v_i の代わりに v_i と書くと) Σ_{v_i>δ} δ_i ≦ Σ_i=1ⁿ (d_i - c_i) < ε.□

定理 [線型性]:

区間 I に於いて, p を定数とすると
f(x), g(x) が可積 ⇒ f(x) + g(x), pf(x) は可積

積分区間 I の分割 Δ に関して, 前のように c_k ∈ I_k として

Σ_k=1ⁿ(f(c_k) + g(c_k))δ_k = Σ_k=1ⁿ f(c_k)δ_k + Σ_k=1ⁿ g(c_k))δ_k,
Σ_k=1ⁿ pf(c_k)δ_k = pΣ_k=1ⁿ f(c_k)δ_k,

だから (つまり単なる Σ の線型性に帰結される)。□

定理:

区間 I に於いて
f(x), g(x) が可積 ⇒ f(x)g(x) は可積

証明: 今まで f(x) の上限, 下限を M, m で表してきたが, それに対応して, g(x) の方は各々 K, k で表すものとする。 更に f(x)g(x) の方は Q, q で表そう。又 F(x) = f(x) - k ≧ 0, G(x) = g(x) - k ≧ 0 と置くと f(x)g(x) = (F(x) + m)(G(x) + k) = F(x)G(x) + kF(x) + mG(x) + mk であるから, 最初から f(x) ≧ 0, g(x) ≧ 0 であると仮定して証明すればよい。 このとき先ず q_i ≧ m_ik_i, Q_i ≦ M_iK_i であって

Q_i - q_i ≦ M_iK_i - m_ik_i = M_i(K_i - k_i) + k_i(M_i - m_i) ≦ M(K_i - k_i) + k(M_i - m_i)

これから sup, inf に移って

S_Δ(fg) - s_Δ(fg) ≦ M(S_Δ(g) - s_Δ(g)) + m(S_Δ(f) - s_Δ(f)).

ここで f, g が可積だから δ(Δ)→0 の時, 右辺→0 だから。□

定理:

閉区間 I で f(x) が可積で |f(x)| ≧ d > 0 ⇒ 1/f(x) も可積。

S_Δ(1/f) - s_Δ(1/f) = Σ v_k(1/f)δ_k ≦ Σ (v_k(f)/d²)δ_k = (1/d²)(S_Δ(f) - s_Δ(f)) から。

定理:

閉区間 I で f(x) が可積 ⇒ |f(x)| も可積 且つ |∫_a^b f(x) dx| ≦ ∫_a^b |f(x)| dx.

三角不等式から v_k(|f|) ≦ v_k(f) で且つ |Σ f(c_k)δ_k| ≦ Σ |f(c_k)|δ_k だから。

この定理の逆, つまり |f(x)| が可積だからといって f(x) は可積とは限らない。 例えば上記の Dirichlet の函数 f(x) に関し, g(x) = f(x) - 1/2 と置くと, |g(x)| は全ての x で 1/2 という値を採るので, 任意の有限閉区間で可積であるが, g(x) 自体は可積にはならない。 そこで

f(x) と |f(x)| が同時に可積であるとき f(x) は絶対可積という。

すぐ上の定理に述べたように, 有限閉区間で有界な函数 f(x) が可積であるならば絶対可積である。

次へ
積分 3 の目次へ