等差数列とその和

等差数列 arithmetic progression (略して A.P.) とは, 「或る数から始めて, 次々に一定の数を加えて得られる数列」 である。 「等差」 とは隣り合う二つの項の差を取ると, いつも一定数だからそう呼ばれるわけである。

この前の項に次々に加えられていく一定の数のことを公差 common difference といい, 普通 d と書かれる。

等差数列の一般項がどうなっているかを見てみよう。 初項 a₁ は与えられているとする。

a₂ = a₁ + d が定義 (手前の項に公差 d を足す) から分かる。 以下同様にして, それまでに分かっている項を代入していく。

(次の項は, 前の項に公差 d を足したもの, の繰り返し)
a₃ = a₂ + d = (a₁ + d) + d = a₁ + 2d.
a₄ = a₃ + d = (a₁ + 2d) + d = a₁ + 3d.
a₅ = a₄ + d = (a₁ + 3d) + d = a₁ + 4d.
a₆ = a₅ + d = (a₁ + 4d) + d = a₁ + 5d.
a₇ = a₆ + d = (a₁ + 5d) + d = a₁ + 6d.
a₈ = a₇ + d = (a₁ + 6d) + d = a₁ + 7d.
a₉ = a₈ + d = (a₁ + 7d) + d = a₁ + 8d.
a₁₀ = a₉ + d = (a₁ + 8d) + d = a₁ + 9d.
…………………………………………

これでもう大体規則が分かったであろうか ?
a_番号 =  a₁ + (番号より 1 小さい数)d.
という形をしているよね ? 実際

a_n = a₁ + (n - 1)d

というのが, 公差が d である等差数列 {a_n} の一般項の公式である。 実際

a_n+1 = a_n + d = (a₁ + (n - 1)d) + d = a₁ + ((n - 1) + 1)d = a₁ + ((n + 1) - 1)d.

だから数学的帰納法から正しいことが分かる。

さて次に S_n = Σ_{k = 0} ⁿ a_k = a₁ + a₂ + a₃ + a₄ + … + a_n を求めてみよう。 一般に無限数列 {a_n} が与えられていた場合, S_n = Σ_{k = 0} ⁿ a_k は新たな数列を定めていると考えられ, 普通もとの数列の第 n 部分和 the nth partial sum と呼ばれている。

次の方法は Gauß が小学生の時, その先生が授業をやるのが嫌になったとかで, 1 から 100 まで足しなさい, といったときに, 即座にその答えを出した方法を一般化したものである。

というわけで先ず, Gauß がどうやって 1 から 100 までの和を即座に出したかを, 見てみよう。

Gauß はこう考えたらしい。 S = 1 + 2 + 3 + … + 100 としよう。 足算は逆に書いたって同じだから S = 100 + 99 + 98 + … + 1 だ。 これを縦に足してみよう。 つまり

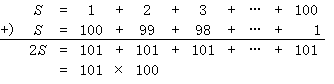
従って S = (101×100)/2 = 101×50 = 5050. これの方が 1 から順に足すより遙かに速い時間で出来る。

勿論どんな数列でも原理的には初項から順に足していけば, 必ず第 n 部分和は求まるわけであるが, 遙かに効率が悪い。 よく考えると, 1, 2, 3, ..., 100 というのも, 等差数列のうちの特別なもの (初項も公差も 1) に過ぎないので, これを一般化することはたやすい。

先ず
S_n = Σ_{k = 0} ⁿ a_k = Σ_{k = 0} ⁿ (a₁ + (k - 1)d)
= a₁ + (a₁ + d) + (a₁ + 2d) + … + (a₁ + (n - 1)d)
だから, これを逆に書くと
S_n = a_n + a_n-1 + a_n-2 + … + a₁
= (a₁ + (n - 1)d) + (a₁ + (n - 2)d) + (a₁ + (n - 3)d) + … + a₁
であることに注意しておくと

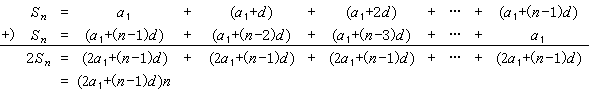
となるので, 即ち

S_n = (2a₁ + (n - 1)d)n/2 = (a₁ + a_n)n/2 を得る。

勿論これを正式に数学的帰納法を用いて証明することも出来るが, 簡単なので読者に任せる。

さて, 三つの数, a, b, c がこの順に等差数列をなしているとすると, 等差数列の定義から, b - a = c - b が公差になる。 この式を移項すると 2b = a + b という式が得られる。 このように三つの数が等差数列をなしているとき, 中央の数は, 残りの数の相加平均で与えられていることが分かる。 そこでこの中央の数のことを等差中項 arithmetic mean と呼ぶ。

さて, 上記の公式を見ると, 等差数列 {a_n} に於いて, a_n が n の一次式, S_n は n の二次式になっている。 ではこの逆は成り立つであろうか ?

そこで p, q を定数として, a_n = pn + q と置こう。

初項 a₁ = p×1 + q = p + q は定数だから良い。

公差は n > 1 の時
d = a_n+1 - a_n = p(n + 1) + q - (pn + q) = pn + p + q - pn - q = p
で定数だからこちらも良い。

即ち数列 {pn + q} は初項 p + q, 公差 p の等差数列である。

和の方は, 公式を見れば分かるように, 定数項が 0 でないと, 等差数列の和にはなり得ない。 従って, r, s を定数として S_n = rn² + sn と置こう。

又あとでも触れると思うが, 第 n 部分和が与えられている数列の場合, 先ず初項は
a₁ = S₁ = r + s
であることはすぐに分かるであろう。 次に n > 1 の場合
a_n = S_n - S_n-1 = rn² + sn - (r(n - 1)² + s(n - 1))
= rn² + sn - (r(n² - 2n + 1) + sn - s)
= rn² + sn - rn² + 2rn - r - sn + s
= 2rn  - r + s.
だから n の一次式になるので良さそうであるが, 一寸気をつけなければいけないのは, これが n = 1 の時に矛盾なく定まっていなければいけないことである。 つまり, あとの方の式では a₁ = 2r - r + s = r + s で, 確かに最初の式と一致している。

従って S_n が等差数列の和であるためには, それが定数項が 0 である n の二次式であることが必要十分である。

尚, 最初から S_n = rn² + sn + t と定数項付きで始めれば a₁ = S₁ = r + s + t となる所だけが違うので, t = 0 であることが分かる。

次へ
数列とその極限の目次へ