等比数列 geometric progression (略して G.P.) とは, 「或る数から始めて, 次々に一定の数を掛けて得られる数列」 である。 「等比」 とは隣り合う二つの項の比を取ると, いつも一定数だからそう呼ばれるわけである。
この前の項に次々に掛けられていく一定の数のことを公比 common ratio といい, 普通 r と書かれる。
等比数列の一般項がどうなっているかを見てみよう。 初項 a1 は与えられているとする。
a2 = a1r が定義 (手前の項に公比 r を掛ける) から分かる。 以下同様にして, それまでに分かっている項を代入していく。
(次の項は, 前の項公比 r を掛けたもの, の繰り返し)
a3 = a2r = (a1r)r = a1r2.
a4 = a3r = (a1r2)r = a1r3.
a5 = a4r = (a1r3)r = a1r4.
a6 = a5r = (a1r4)r = a1r5.
a7 = a6r = (a1r5)r = a1r6.
a8 = a7r = (a1r6)r = a1r7.
a9 = a8r = (a1r7)r = a1r8.
a10 = a9r = (a1r8)r = a1r9.
……………………………
これでもう大体規則が分かったであろうか ?
a番号 = a1r(番号より 1 小さい数),
という形をしているよね ? 実際
an = a1rn - 1
というのが, 公比が r である等比数列 {an} の一般項の公式である。 実際
an+1 = anr = (a1rn - 1)r = a1 r(n - 1) + 1 = a1r(n + 1) - 1.
だから数学的帰納法から正しいことが分かる。
殆ど等差数列と変わらない書き方なのが分かっただろうか ? 実は等差数列の page を copy してきて, 書き直しただけなのだった (笑)。
次に, 第 n 部分和 Sn = Σk = 0 n ak = a1 + a2 + a3 + a4 + … + an を求めてみよう。 こちらは一般項と大分違って, 等差数列よりも格段に難しい (とはいえ覚えてしまえば何のことはない。 置換積分のやり方が非常に沢山あって慣れるのが大変なのに比べれば大したことはない)。
次のは確かエリ・マオールの本のどれかに出ていたと思われる方法。
初項 a 公比 r の等比数列の第 n 部分和の公式の証明:
Sn = a1 + a1r + a1r2 + …… +
a1rn-1
= a1 + a1r + a1r2 + …… + a1rn-1 +
a1rn - a1rn
= a1 + r(a1 + a1r + a1r2 + …… +
a1rn-1) - a1rn
= a1 + rSn - a1rn
= rSn + a1(1 - rn)
より (1 - r)Sn = a1(1 - rn).
取り敢えずここまでで置いておいて, 普通の教科書に載っている方法を紹介しておく。
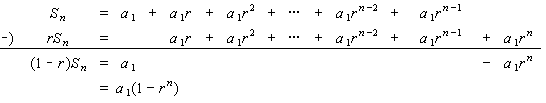
(この方法を S - rS 法と言ったりする。 又あとで出て来る。)
さて, 何れの方法にしても (1 - r)Sn = a1(1 - rn) であることが分かったが, Sn = の形にするには 1 - r で割らなければならない。 当然, これが 0 であると割れないわけだから
r ≠ 1 ⇒ Sn = a1(1 - rn)/(1 - r) = a1(rn - 1)/(r - 1)
(最後の部分は分子と分母に -1 を掛けたのである。 r > 1 の時はこちらの方が便利である。というのは分子も分母も + になるから)。 勿論これを正式に数学帰納法で証明することも出来るが, 簡単なので読者に任せる。
さて, r = 1 だったらどうなるであろうか ? この場合は最初の一般項の所に戻ると, an = a1rn-1 = a1 で実は定数列である。 ということは Sn は同じ a1 の n 個の和なのだから
r = 1 ⇒ Sn = a1n
ということになる。 因みに, 定数列は初項 a1, 公差 0 の等差数列とも見ることが出来るので, この公式が正しいことは, 等差数列の和の公式からも分かる。
どの数も 0 でない三つの数 a, b, c がこの順に等差数列を成しているとしよう。 この場合, 等比数列の定義から, 公比 b/a = c/b が公比になる。 分母を払うと b2 = ac と中央の項が簡単に求まるので, 等差数列の時と同様に中央の数のことを等比中項 geometric mean と呼ぶ。