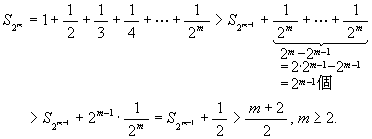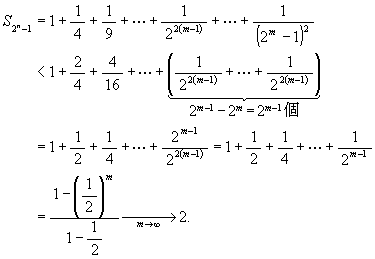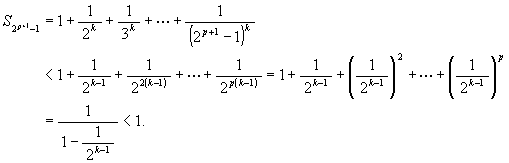全ての項が負ではないような無限級数を, 正項級数 series with positive terms, series of positive terms, positive series という。
[定理]
Σn=1∞an, Σn=1∞bn が正項級数で, 全ての n に関し an ≧ bn (≧ 0) であるとき, 級数 Σn=1∞an が収束してその和が A ならば, 級数 Σn=1∞bn も収束してその和 B は A を超えない。 即ち A ≧ B.
この定理の対偶を取ると 級数 Σn=1∞bn が発散すると, Σn=1∞an も発散するということである。
[証明]
An = Σk=1nak, Bn = Σk=1nbk と置くと明かに An ≧ Bn. 仮定から An - An-1 = an ≧ 0 より An は (広義) 単調増加であるから Bn ≦ An ≦ limn→∞An = A.
An と同様にして Bn も (広義) 単調増加で, 上記から上に有界で, その上限の一つが A だから, 定理によって数列 {Bn} は収束する。 従って, その和 B に対し B ≦ A が成立する□
例) 次の無限級数の収束, 発散を調べよ。
(1) Σn=1∞ 1/n.
(2) Σn=1∞ 1/n!.
(3) Σn=1∞ 1/n2.
(4) Σn=1∞ 1/√n.
解) 以下では与えられた無限級数の第 n 部分和を Sn とする。
(1) S1 = 1 = 2/2,
S2 = 1 + 1/2 = 3/2,
S4 = 1 + 1/2 + 1/3 + 1/4 > S2 + 1/4 + 1/4 = S2
+ 1/2 = 4/2,
S8 = 1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 > S4 +
1/8 + 1/8 + 1/8 + 1/8 = S4 + 1/2 > 4/2 + 1/2 = 2/5,
.................................................................................
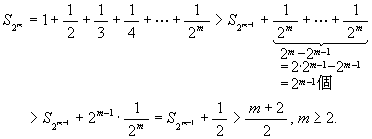
ここで, 2m ≦ n < 2m+1 となる整数 n
をとると, Sn は (狭義) 単調増加だから
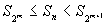が成り立ち, 
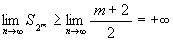であるから, limn→∞Sn = +∞. つまり Σn=1∞ 1/n
は発散する。
この方法は基本的に 1350 年頃にフランスのオーレムという人が証明した方法であるということである。 [黒川信重, 数学セミナー (10), 2003]
[別解 1] Cauchy の収束判定法を用いると
Σk=12n 1/k - Σk=1n 1/k = 1/(n + 1) + 1/(n + 2) + … + 1/(2n) > 1/(2n)×n = 1/2
だから発散する。
[別解 2] 些か姑息だが, 積分と比較する (しかし簡単ではある)。
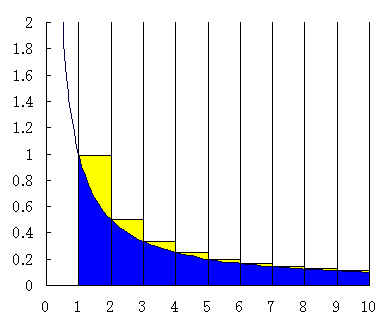
図には y = 1/x の graph が描いてある。 青く塗った部分が, y = 1/x と x 軸, x = 1 で囲まれた部分。 青く塗った部分と, 黄色く塗った部分の面積が Σn=1∞ 1/n に対応する。
さて図から分かるように Σk=1n 1/k > ∫1n dx/x = [log x]1n = log n - log 1 = log n → ∞ as n → ∞ だから発散する。
(2) S1 = 1,
S2 = 1 + 1/2,
S3 = 1 + 1/2 + 1/3! < 1 + 1/2 + 1/22,
S4 = 1 + 1/2 + 1/3! + 1/4! < 1 + 1/2 + 1/22 + 1/23,
........................................................................................
Sn = 1 + 1/2 + 1/3! + … + 1/n! < 1 + 1/2 + 1/22 + …
+ 1/2n-1 = (1 - (1/2)n)/(1 - 1/2) = 2(1 - (1/2)n)
< 2, n ≧ 3.
0 < S1 < S2 < … < Sn < … … < 2
即ち {Sn} は上方に有界な (狭義) 単調増加数列だから収束する。
以前に Taylor 展開 の [1] で掲げたように, この和は実は e - 1 になる。
(3) S1 = 1,
S3 = 1 + 1/4 + 1/9 < 1 + 1/4 + 1/4 = 1 + 2/4 = 3/2,
S7 = 1 + 1/4 + 1/9 + 1/16 + 1/25 + 1/36 + 1/49 < 1 + 2/4 +
4/16 = 1 + 1/2 + 1/4,
S15 = 1 + 1/4 + 1/9 + 1/16 + 1/25 + 1/36 + 1/49 + 1/64
+ 1/81 + 1/100 + 1/121 + 1/144 + 1/169 + 1/196 + 1/225 < 1 + 2/4 + 4/16 +
8/64 = 1 + 1/2 + 1/4 + 1/8,
...................................................................................
(m ≧ 2 の時)
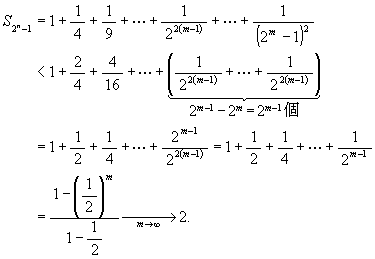
又 2m - 1 ≦ n < 2m+1 - 1 を採ると n ≧ 2
では Sn - Sn-1 = 1/n2 > 0 で (狭義)
単調増加であるから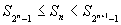 
< 2 となるので収束する。
尚, 下記参照のこと。
(4) 一般に n2 ≧ n > 0 だから n ≧ √n > 0. 即ち 1/n ≦ 1/√n.
∴Σn=1∞ 1/√n ≧ Σn=1∞ 1/n = +∞. よって発散する。
実は Σn=1∞ 1/nk, k > 0 は k > 1 の時収束し, 0 < k ≦ 1 の時発散する。
[略証]
k > 1 ⇒ 1/(2p)k + 1/(2p + 1)k + … + 1/(2p+1 - 1)k < 2p/(2p)k = 1/(2p)k-1 より
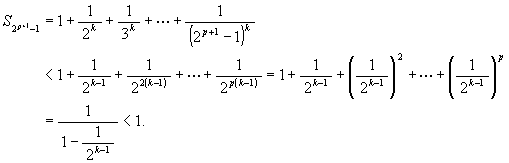
で, 上方に有界な (狭義) 単調増加数列となるから。
又 0 < k ≦ 1 ⇒ 1/nk ≧ 1/n より (4) と同様に発散する。
ζ(s) = Σn=1∞ 1/ns と書いて Riemann (リーマン) のゼータ函数 zeta function という。 s が自然数で偶数のときは値が知られていて ζ(2) = π2/6, ζ(4) = π4/90, ζ(6) = π6/945. 一般に n を自然数, Bn を Bernoulli 数 (ベルヌーイ数, まだこの site では説明していない) とすると ζ(2n) = (2π)2nB2n/(2(2n)!) となることが知られている。 これを証明するにはまだこの site で説明していない technique を必要とするので, ここでは証明しない。
筆者は未読ではあるが, 参考書として
荒川恒男, 伊吹山知義, 金子昌信: ベルヌーイ数とゼータ関数, 牧野書店
を掲げておく。
次へ
無限級数の目次へ