所謂 「余弦定理」 である。 最初に Euclid 原論に出てくる次の定理を証明しよう (II 13)。
定理 1
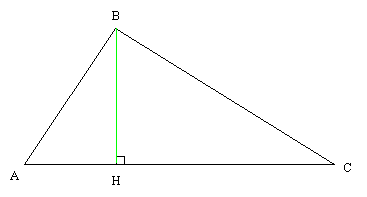
△ABC に於て ∠BAC は鋭角とする。 この時頂点 B から対辺 AC に引いた垂線の足を H とすると
BC2 = AB2 + AC2 - 2AC・AH.

証明: 三平方の定理 (Pythagoras) によって
BC2 = BH2 + HC2,
AB2 = BH2 + AH2.
辺々引いて
BC2 - AB2 = HC2 - AH2 = (HC + AH)(HC
- AH) = AC(HC - AH) = AC((AC - AH) - AH)
= AC(AC - 2AH) = AC2 - 2AC・AH□
鈍角の時も Euculid 原論に次の定理が出ている (II 12)。
定理 2
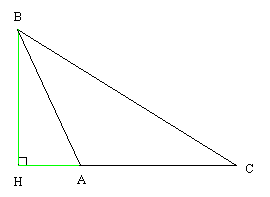
△ABC に於て ∠BAC は鈍角とする。 この時頂点 B から対辺 AC に引いた垂線の足を H とすると
BC2 = AB2 + AC2 + 2AC・AH.
証明, 前と同様に
BC2 = BH2 + HC2,
AB2 = BH2 + AH2.
より辺々引いて
BC2 - AB2 = HC2 - AH2 = (HC + AH)(HC
- AH) = (HA + AC + AH)AC = (AC + 2AH)AC
= AC2 + 2AC・AH□
さて, 余弦函数の定義から, 定理 2 で -AH = ABcos ∠BAC であり, ∠BAC = π/2 の時も, AH = ABcos ∠BAC = 0 で, この場合は三平方の定理が成り立つので, 一般に次の定理が成立することが分かった:
△ABC に対し
BC2 = AB2 + AC2 - 2AC・AB cos ∠BAC.
(余弦函数の鈍角の符号は, これが成り立つように拡張されたものと思っても良い。) この第二余弦公式は, ある一つの辺 (ここでは BC) が残りの辺の長さと対角の大きさで決まることを述べている式だと思って良い。 尚, 普通 「余弦公式 (余弦定理)」 というと, この第二余弦公式のことをさす。
更に, 次の定理が成立する
△ABC に対し
AC = AB cos ∠BAC + BC cos ∠BCA.


図からも証明できるが, 第二余弦公式からも証明できる。 第二余弦公式から
cos ∠BAC = (AB2 + AC2 - BC2)/(2AC・AB),
cos ∠BCA = (BC2 + AC2 - AB2)/(2AC・BC)
(後ろの方の式は, 上の式で A と C を入れ替えればいい) なので, これらから
AB cos ∠BAC + BC cos ∠BCA
= AB(AB2 + AC2 - BC2)/(2AC・AB) + BC(BC2
+ AC2 - AB2)/(2AC・BC)
= (AB2 + AC2 - BC2)/(2AC) + (BC2 +
AC2 - AB2)/(2AC)
= (AB2 + AC2 - BC2 + BC2 + AC2 - AB2)/(2AC)
= 2AC2/(2AC) = AC□
逆に, 第一余弦公式から, 第二余弦公式を導くことも出来る。 先ず, 第一余弦公式を A→B→C→A と巡回的に文字を入れ替えて成り立つ次の二つの公式
BC cos ∠CBA + CA cos ∠CAB = BA,
CA cos ∠ACB + AB cos ∠ABC = CB
とを合わせて cos に関する連立方程式と思う。 先ず, 定理のところに書いた式を AC 倍し, 今書いた式の下の方の式を BC 倍して引算する。
AB・AC cos ∠BAC - AB・BC cos ∠ABC = AC2 - BC2.
さっき二つ書いた上の方の式から BC cos ∠ABC = BA - CA cos ∠CAB であるからこれを代入して
AB・AC cos ∠BAC - AB(BA - CA cos ∠CAB) = AC2 - BC2.
即ち 2AB・AC cos ∠BAC - AB2 = AC2 - BC2.□