ここで数学の一般常識として,
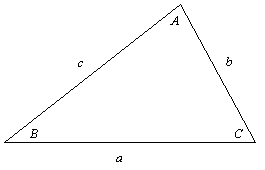
△ABC に於いて, ∠A の大きさを唯単に A, 同様に ∠B を B, ∠C を C と, 又, 辺 BC の長さを (対角の記号を用いて) a, 辺 CA
を b, 辺 AB を c と略記することに注意しておく。△ABC の外心 E の位置ベクトルを求めてみよう。
ここで数学の一般常識として,
△ABC に於いて, ∠A の大きさを唯単に A, 同様に ∠B を B, ∠C を C と, 又, 辺 BC の長さを (対角の記号を用いて) a, 辺 CA
を b, 辺 AB を c と略記することに注意しておく。
二つの vectors AB, AC は明らかに一次独立である (平行でない)
から, 実数 s, t を用いて
AE = s AB + t AC……(1)
と書ける。
この s と t とを求めれば良いわけである。
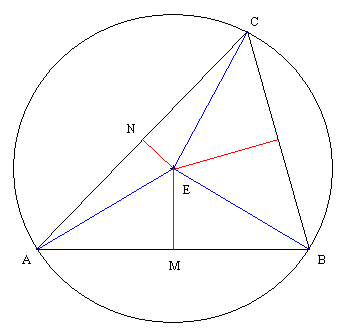
外心は各辺の垂直二等分線の交点であるから特に ME⊥AB,
NE⊥AC.
従って
ME・AB = (AE - AM)・AB = (s
AB + t AC - AB/2)・AB
= (s - 1/2)|AB|2 + tAB・AC
= (s - 1/2)c2 + t bc cos A = 0.
同様に
NE・AC = s bc cos A + (t - 1/2)b2 = 0.
従って s, t に関する連立方程式
c2 s + (bc cos A) t = c2/2,……(2)
(bc cos A) s + b2 t = b2/2……(3)
を得る。
(2)b2 - (3)(bc cos A):
(b2c2 -
(bc cos A)2)s = (b2c2 - b3c cos
A)/2.
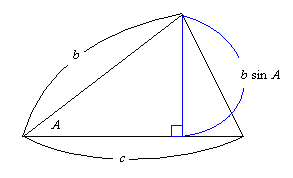ここでいつものように
S を △ABC の面積とする。
この時良く知られているように
S = (bc sin A)/2
= (ca sin B)/2
= (ab sin C)/2
が成立する。
従って s の係数は
b2c2 - (bc cos A)2 =
b2c2(1 - cos2A) =
b2c2sin2A = 4×((bc sin A)/2)2 = 4S2
(≠0)
であるから, (第二) 余弦公式 2bc cos A = b2 + c2
- a2 を用いて
s = (b2c2 - b3c cos A)/(8S2) = (2b2c2 -
2b3c cos A)/(16S2)
= b2(2c2 -
2bc cos A)/(16S2) = b2(2c2 - (b2 + c2
- a2))/(16S2)
= b2(c2 + a2 - b2)/(16S2).
同様に
t = c2(a2 + b2 - c2)/(16S2).
これらを (1) に代入して
AE = [b2(c2 + a2 - b2)AB + c2(a2 + b2 - c2))AC]
/(16S2).
位置ベクトルで書き直して E(p) とすると
p - a = [b2(c2 + a2 - b2)(b
- a) + c2(a2 + b2 - c2))(c
- a)]/(16S2).
∴p = [(16S2 - b2(c2 + a2 - b2) - c2(a2 + b2 - c2))a + b2(c2 + a2 - b2)b + c2(a2 + b2 - c2))c]/(16S2).
ここで a の係数の 16S2 倍に着目すると
16S2 - b2c2 - a2b2 + b4
- a2c2 - b2c2 + c4
= 16×((ac sin B)/2)2 - a2c2 - a2b2 -
2b2c2 + b4
+ c4
= 4a2c2sin2B - a2c2 - a2b2 -
2b2c2 + b4
+ c4
= 4a2c2(1 - cos2B) - a2c2 - a2b2 -
2b2c2 + b4
+ c4
= 3a2c2 - (2ac cos B)2 - a2b2 -
2b2c2 + b4
+ c4
= 3a2c2 - (a2 + c2 - b2)2 - a2b2 -
2b2c2 + b4
+ c4 ……ここで, (第二) 余弦公式を用いた
= 3a2c2 - (a4 + c4 + b4
+2a2c2 -
2b2c2 - 2a2b2) - a2b2 -
2b2c2 + b4
+ c4
= 3a2c2 - a4 - 2a2c2 +
2b2c2 + 2a2b2 - a2b2 -
2b2c2
= a2b2 + a2c2 - a4
= a2(b2 + c2 - a2).
以上から結局
p = [a2(b2 + c2 - a2)a + b2(c2 + a2 - b2)b
+ c2(a2 + b2 - c2))c]/(16S2).
(素晴らしく美しい対称性 !)
尚, これを用いて再び ((a + b)/2 - p)⊥(b - a) を証明することも出来る。
今度は頂点 C, B から対辺 (またはその延長上) に降ろした垂線の足を各々 P, Q とする。
この時 H = (B∪Q)∩(C∪P) と置くと (A∪H)⊥BC が知られていて, この点 H を垂心 orthocentre という。
![[垂心の図]](orthocentre.gif)
今度はこの垂心の位置ベクトルを求めてみよう。 外心のときと同様に AH = sAB + tAC と書ける。
図より AP = ((b cos A)/c)AB であるから
PH = AH - AP = (s - ((b cos A)/c))AB
+ tAC.
PH・AB = (s - ((b cos A)/c))c2 + (bc cos A)t = 0.
同様にして
QH・AC = (bc cos A)s + (t - ((c cos A)/b))b2 = 0.
従って次の連立方程式を得る:
c2s + (bc cos A)t = bc cos A = (b2 + c2 - a2)/2,
(bc cos A)s + b2t = (b2 + c2 - a2)/2.
左辺側は外心のときと同様であるから
s = ((b2 + c2 - a2) / 8S2)(b2 -
bc cos A)
= ((b2 + c2 - a2) / 16S2)(2b2 -
2bc cos A)
= ((b2 + c2 - a2) / 16S2)(a2 + b2 - c2).
t = ((b2 + c2 - a2) / 8S2)(-
bc cos A + c2)
= ((b2 + c2 - a2) / 16S2)(2c2 -
2bc cos A)
= ((b2 + c2 - a2) / 16S2)(c2 + a2 - b2).
故に
AH = (b2 + c2 - a2)[(a2 + b2 - c2)AB
+ (c2 + a2 - b2)AC]/16S2
従って H(h) とすると
h = [(a2 + b2 - c2)(c2 + b2 - a2)(b - a) + (b2 + c2 - a2)(c2 + a2 - b2)(c - a) + 16S2a]/16S2.
ここでも外心のときのように a の係数の 16S2
倍のみに着目すると
16S2
- (a2 + b2 - c2)(c2 + b2 - a2)
- (b2 + c2 - a2)(c2 + a2)
= 16S2
- (b2 + (a2 - c2))(b2 - (a2 - c2))
- (c2 + (b2 - a2))(c2 - ( b2 - a2))
= 16S2
- (b4 - a4 - c4 + 2a2c2)
- (c4 - b4 - a4 + 2a2b2)
= 16S2
+ 2a4 - 2a2c2 - 2a2b2
= 4a2c2sin2B
+ 2a4 - 2a2c2 - 2a2b2
= 4a2c2(1 - cos2B)
+ 2a4 - 2a2c2 - 2a2b2
= 2a4 + 2a2c2 - 2a2b2 -
(2ac cos B)2
= 2a4 + 2a2c2 - 2a2b2 -
(a2 + c2 - b2)2
= 2a4 + 2a2c2 - 2a2b2 -
(a4 + b4 + c4 - 2a2b2 - 2b2c2
+ 2c2a2)
= a4 - b4 - c4 + 2b2c2
= a4 - (b2 - c2)2
= (a2 - b2 + c2)(a2 + b2 - c2).
以上より
h = [(c2 + a2 - b2)(a2 + b2 - c2)a
+(a2 + b2 - c2)(c2 + b2 - a2)b
+ (b2 + c2 - a2)(c2 + a2
- b2)c]/16S2.
(再び美しい対称性 !)
これから (a - b)⊥h が証明できるので, 垂心とは, 頂点から対辺に引いた三垂線の交点であることが証明される。