x
軸対称変換以下一次変換のうちのいくつかの例を成分表示で表してみよう。
一番簡単な変換は a = 1, b = 0, c = 0, d = 1 という変換である。 即ち
x' = x,
y' = y
である。 これは実際には像と原像が一致している。 この変換を
恒等変換 identity transformation
という。
a = b = c = d = 0 であるような変換, 即ち
x' = 0,
y' = 0
という特殊な変換も亦一次変換の一種である。 普通像全体の集合が一点からなるものを定値写像というが, この変換は一次変換のうち唯一の定値写像である。 というのはもしも, 任意の x について f(x) = a であったとすると線型性から f(2x) = f(x) = 2a でなければならないから, 定値写像であるから 2a = a でなければならず, それは a = 0 を意味している。
この変換は零変換 null transformation という。
x
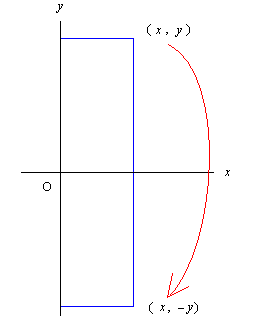
軸対称変換点を x 軸に関し対称に変換するものを考える。
この変換は右図に見られるように
(x, y) → (x, -y)
という変換を引き起こしている。
これを標準形で表すと
x' = x,
y' = -y
となっている。
これを x 軸対称変換という。
同様に点を y 軸に関し対称に変換するものを考える。
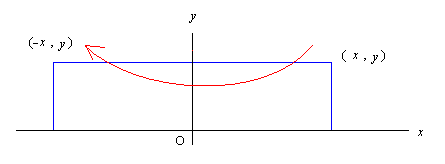この変換は右図に見られるように
(x, y) → (-x, y)
という変換を引き起こしている。
これを標準形で表すと
x' = -x,
y' = y
となっている。
これを y 軸対称変換という。
原点対称変換更に点を原点に関し対称に変換するものを考えると, 右図に見られるように
(x , y) → (-x, -y)
というものであるので,
x' = -x,
y' = -y
となる。
これを原点対称変換という。
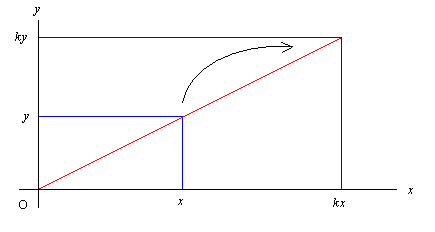原点を中心として k (> 0) 倍の拡大をする変換を考える。 この変換は図に見られるように
(x, y) → (kx, ky)
というものなので,
x' = kx,
y' = ky
となる。
これを原点を中心とする相似比 k の相似変換という。
この辺から一寸難しい。
原点中心の角度 θ (一般角で採る) の回転変換を考える。
一次変換の所で示したように, この変換 f は f(ex) と f(ey) だけで定まる。
右図に見られるように
f(ex) = cos θ ex
+ sin θ ey,
f(ey) = -sin θ ex + cos θ ey
であるから,
x' = (cos θ)x - (sin θ)y,
y' = (sin θ)x + (cos θ)y
となっている。
これが原点中心角度 θ の回転変換である。
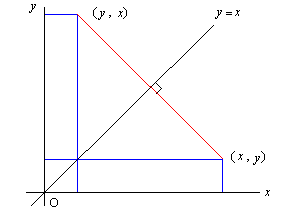この変換は右図に見られるように
(x, y) → (y, x)
という変換になるので
x' = y,
y' = x
である。
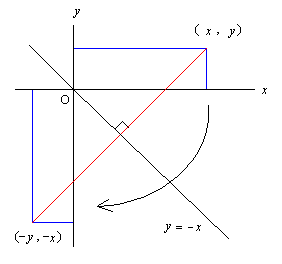
この変換は右図に見られるように
(x, y) → (-y,- x)
という変換になるので
x' = -y,
y' = -x
である。
平面上の点 P0(x0, y0) の直線 y = mx に関する対称点を P'(x', y') とする。 直線 y = mx は mx - y = 0 と書けるので, その方向ベクトル (の一つ) は (1, m) である。 明らかに
P0P' ⊥ (1, m) ⇔ (x' - x0, y' - y0)・(1, m) = 0.
従って x' - x0 + my' - my0 = 0. 故に
x' + my' = x0 + my0 … (1).
さて又, P0 と P' の中点 ((x' + x0)/2, (y' + y0)/2) は直線 y = mx 上にあるので (y' + y0)/2 = m(x' + x0)/2. 故に
mx' -y' = -mx0 + y0 … (2).
(1) と (2) を連立させると m2 + 1 > 0 なので
x' = ((1 - m2)/(1 + m2))x0 +
(2m/(1 + m2))y0,
y' = (2m/(1 + m2))x0 - ((1 - m2)/(1 + m2))y0.
これを書き改めて
x' = ((1 - m2)/(1 + m2))x + (2m/(1 + m2))y,
y' = (2m/(1 + m2))x - ((1 - m2)/(1 + m2))y.
これが求めるものである。