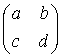に翻訳する。
f°f-1 = f-1°f
= IA から写像 f: A→B に対し g: B→A が存在して
∀y = f(x): g(y) = x
となるとき g を f の (左) 逆写像 (left) inverse mapping という (右逆写像というものがどういうものであるべきかは容易に想像がつくであろう)。 この時直ちに分かることは
[1] f が (左) 逆写像を持てば f(x1) = f(x2) ⇒ x1 = x2.
[2] f の (左) 逆写像が g で f(A) = B ⇒ g の (左) 逆写像が f.
但し f(A) = {f(x)| x ∈ A}.
このことから次のように名付ける:
定義
f(x1) = f(x2) ⇒ x1 = x2 の成立する写像 f を単射 injection, monomoriphism,
f(A) = B の成立する写像 f を全射 surjection, epimorphism という。
全射且つ単射である写像を全単射 bijection という。
又, f の (左) 逆写像を f-1 と書く。 [2] より f が全射の時 (f-1)-1 = f である。
今 IA:A→A を A 上の恒等変換, 即ち IA(x) = x とすると, f が全単射ならば明らかに f-1 が存在し
f°f-1 = f-1°f = IA
が成立する。
以上のことは f, g が特に一次変換の場合にも成立する。 この場合変換だから逆写像のことを逆変換という。
さて今, 一次変換 f を
x' = ax + by … (1),
y' = cx + dy… (2)
と置いて, f の逆変換 f-1 を求めてみよう。
先ず y を消去するために (1)×d - (2)×b を計算すると
dx' - by' = (ad - bc)x … (3).
同様に x を消去するために (1)×a - (2)×c を計算すると
-cx' + ay' = (ad - bc)y … (4).
従って
ad - bc ≠ 0
ならば
x = (d/(ad - bc))x' - (b/(ad - bc))y',
y = -(c/(ad - bc))x' + (a/(ad - bc))y'
がえられる。 これが求める逆変換の式である。
というわけで
定義
det(f) = ad - bc
を一次変換 f の行列式 determinant という。
つまり, 一次変換 f はその行列式 det(f) ≠ 0 の時逆変換 f-1 を持つ。. そして全ての (x', y') ∈ R 2 に対し, f の原像は上記の式で計算できるから, f は全射でもある。
従って
[定理]
平面上の一次変換 f が逆変換を持つための条件は
det(f) ≠ 0
で, しかもこの時 f は全単射。
又 det(f) = 0 の時は (3), (4) から
dx' - by' = 0,
-cx' + ay' = 0
であるが ad - bc = 0 即ち ad = bc 故 a : c = b : d であるから, これらは実は同一の式である。 従って
[定理]
平面上の一次変換 f を表す式 (1), (2) が与えられているとき, f が逆変換を持たないためには
det(f) = 0
が必要十分で, この時 f の像は f が零変換の時は一点 (0, 0), そうでないときは直線で, それは
dx' - by' = 0,
cx' - ay' = 0の内 trivial でない方の式を満たす (trivial な式とは, 式として 0 = 0 のこと)。 両方とも non-trivial な場合は, 一方は他方の定数倍になっている。
以上のことを行列 A =
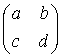に翻訳する。
f°f-1 = f-1°f
= IA から
AX = XA = I2
を満たす行列 X を A の逆行列 inverse matrix といい, A-1 と書く。 A が逆行列を持つための必要十分条件は
det(A) =
= ad - bc ≠ 0
で, この時
A-1 =
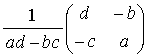
である。 この det(A) は A の行列式 determinant と呼ばれる。
逆変換を持つ変換 f, 従って det(f) ≠ 0, 及び逆行列を持つ行列 A, 従って det(A) ≠ 0 は
正則 regular 又は非退化 non-degenerate
であるといい, det(f) = 0, det(A) = 0 である変換 f, 行列 A は退化している degenerate, 或いは正則でない non-regular といわれる。
次のことは直ぐ分かるだろう:
A: 正則 ⇒ (A-1)-1 = A,
A, B: 正則 ⇒ (AB)-1 = B-1A-1,
A ≠ 0, B≠ 0, AB = 0 ⇒ A も B も退化している。
最後のものだけ証明しておこう:
A: 正則, B≠ 0, AB = 0
⇒ A-1(AB) = A-10
⇒ (A-1A)B = 0
⇒ I2B = 0
⇒ B = 0 は矛盾。
B: 正則, A ≠ 0, AB = 0 の時も同様に矛盾するから□
定理
A, B が正則ならば AB も正則で (AB)-1 = B-1A-1.
証明:
(B-1A-1)AB = B-1(A-1A)B = B-1I2B = B-1B = I2.□
Pontrjagin (ポントリャーギン) 連続群論第一章に拠れば:
AX, XA が定義されていて XA = I2 ⇒ AX = I2.
証明:
X の左逆行列を Y とすると, (XA = I2 だからそれは存在して)
XA = I2 ⇒ XAX = X ⇒ YXAX = YX ⇒ AX = I2□