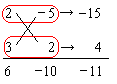
一変数二次式の因数分解として知られている三つの方法について紹介する。
6x2 - 11x - 10 を因数分解しよう。
6x2 - 11x - 10 = (ax + b)(cx + d) と因数分解されたとすると, 右辺は acx2 + (ad + bc)x + bd であるから, ac = 6, bd = -10 から上手く ad + bc = -11 になる組み合わせを見つけようというのが, 襷掛と呼ばれる昔から知られている方法である。 必ず出来るが結構大変である。
ac = 6 だから (a, c) = (1, 6), (6, 1), (2, 3), (3, 2) の 4 つの組み合わせがある (こちらは - を考える必要はない)。 又 bd = -10 だから (b, d) = (1, -10), (-1, 10), (10, -1), (-10, 1), (2, -5), (-2, 5), (5, -2), (-5, 2) の 8 通りの組み合わせがある。都合 32 通りのうち一通りを見つけなくてはいけない。
1 1 → 6
×
6 -10 → -10
-------------
6 -10 -4
この図は, ×の直線に従って 1 × (-10) = -10, 6 × 1 = 6 と矢印の方に書き, 縦に見て 1 × 6 が (二次の係数) 6, 1 × (-10) が (定数項) -10, 一番右の縦が, 6 + (-10) = -4 だが, これは一次の係数 -11 と一致してないので失敗である。 そもそも 6 と -10 のように, 同じ数で割り切れる組み合わせが×の前後で上, 又は下の横で出て来てはいけないのである (後の方を見れば分かる)。 因みに -1 と 10 にしても, -4 が 4 になるだけなので何れにしろ失敗である。
とりあえず, 真ん中の縦だけを逆にしてみよう。
1 -10 → -60
×
6 1 → 1
---------------
6 -10 -59
これも失敗。
1 2 → 12
×
6 -5→ -5
--------------
6 -10 7
これも失敗。 ということを延々とやっていくのだが, この辺は自分でやってもらうとして, 一寸飛ばして
2 5→ 15
×
3 -2→ -4
-------------
6 -10 11
で ± だけ違うから, 真ん中の縦を -5 と 2 に入れ替えればいい。
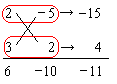
この完成した図で, 赤で囲んだ所を横に見て, 次のように因数分解が完成する。
6x2 - 11x - 10 = (2x - 5)(3x + 2).
慣れてくれば図を描かなくても, 襷掛が出来るようになる。
これは聞く所によるとアメリカの高校生が考えた方法であるとのことである。
同じ 6x2 - 11x - 10 を因数分解してみよう。
この式が因数分解できないのは, 二次の係数が平方数 (或整数の自乗の数) でないからである。 これに何か整数を掛けて平方数を作ろうと思ったら, 6 を掛けるしかない。 しかし等号を成立させる為には同時に 6 で割らねばならない。 つまり
6x2 - 11x - 10 = 6(6x2 - 11x - 10)/6.
最初の 6 だけ括弧の中にいれよう。 すると
6x2 - 11x - 10
= (36x2 - 11×6x - 60)/6
= ((6x)2 - 11(6x) - 60)/6.
ここで t = 6x と置くと
6x2 - 11x - 10 = (t2 - 11t - 60)/6.
これを因数分解するには, 掛けて -60, 足して -11 である二つの整数の組を見つければいい。 60 は 1×60, 2×30, 3×20, 4×15, 5×12, 6×10, という分解を持つから, この中で差が 11 になるのを探すと, それは 4×15. 従って, 符号を考えて,
6x2 - 11x - 10
= (t + 4)(t - 15)/6
= (6x + 4)(6x - 15)/6
= (2(3x + 2))(3(2x - 5))/6
= 2×3(3x + 2)(2x - 5)/6
= (3x + 2)(2x - 5).
というわけで因数分解できた。
これは二次の係数が最初から平方数の場合, そのまま出来る場合と, これのように同じものを掛けて割らなければならない場合と, 二通りあるので, 必ずしも簡単ではない。
二次方程式の解の公式を用いて解く方法。 但し, 平方根が開平出来ないと, この方法は無力である。
先ず, 二次方程式の解の公式について解説する。
x に関する二次方程式 ax2 + bx + c = 0 を monic な (即ち最高次の係数が 1 である) 方程式にする為に, 両辺を a で割る (二次方程式だから二次の係数 a は 0 ではない)
![]()
ここで乗法公式
(x + y)2 = x2 + 2xy + y2
を思い出してもらって先程の方程式を (x + y)2 + z = 0 の形にする。 即ち
![]()
辺々 x の同じ次数の所同士比較すると
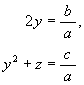
でなければならないことが分かる。即ち
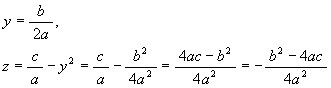
従って,
![]()
移項して平方根を採ると
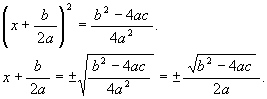
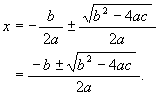
これを二次方程式の解の公式 (根の公式) という。
非常に難しいが三次方程式の解の公式, 四次方程式の解の公式というのも存在する。 しかし五次以上の方程式の一般的な解の公式は存在しない。
さて, x に関する二次方程式 ax2 + bx + c = 0 に於いて, その解が α, β であるとしよう。 解としてα, β を持つような最も簡単な x に関する二次方程式は言うまでもなく
(x - α)(x - β) = 0
である。 この方程式を展開して x に関する同類項で纏めれば
x2 - (α + β)x +αβ = 0
である。 これを最初の方程式と比較すると, 二次の係数が明らかに違うので, そこだけをあわせる為に a を両辺に掛けると
ax2 - a(α + β)x +aαβ = a(x - α)(x - β) = 0.
即ち今次の定理が得られた。
定理
x に関する二次方程式 ax2 + bx + c = 0 に於いて,
その解が α, β であるとすれば
ax2 + bx + c = a(x - α)(x - β).
以上のことから, 解の公式から解を求めて, 上の定理を用いて因数分解できることが分かった。
先程の例をこれを用いて因数分解してみよう。
6x2 - 11x - 10 = 0 と置いて, 解の公式を用いると,
x = (-(-11) ± √((-11)2 - 4×6×(-10)))/(2×6)
= (11 ± √(121+240))/12
= (11 ± √361)/12.
ここで 192 = 361 を知らないときつい。 私の年代でもなかなか知らない開平法 (筆算で平方根を求める方法) を用いるとこれは計算できるが, まぁ電卓でこの辺はやってもらうか, こうなったら諦めて他の方法を採った方が得策というものである。
さて, それが分かっていたとして, 結局
x = (11 ± 19)/12.
+ の方を採ると x = 30/12 = 5/2.
- の方を採ると x = -8/12 = -2/3.
従って
6x2 - 11x - 10 = 6(x - (5/2))(x - (-2/3))
= 6((2x - 5)/2)((3x + 2)/3)
= 6(2x - 5)(3x + 2)/(2×3) = (2x - 5)(3x + 2).
当然だが, 前二つの方法と同じ結果を得る。
実は, この場合に限っては, 192 = 361 を次のようにして調べることができる。 つまり 100 < 361 < 400 だから, とにかくその数は十幾つかであることが分かる。 12 = 1, 22 = 4 と調べていくと, 一桁目が 1 になるのは 12 = 1 と, 92 = 81 しかない。 112 = 121 だから, きっと 192 だろうと思って調べれば, これが正解。
準備の目次へ。