小学校で習ったであろう面積の復習。
[長方形 rectangle]
長方形の定義は四つの角が直角である四角形。 これの面積は覚えているよね。 縦×横だ。

[平行四辺形 parallelogram]
平行四辺形の定義は二組の対辺が互いに平行な四角形。 これの面積は底辺×高さ。 図のように cut して移動すれば長方形になるから。

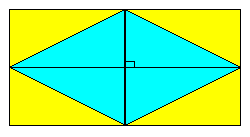
[菱形 rhombus]
菱形の定義は四辺の長さが皆等しい四角形。 平行四辺形の特別なものだが, 二つの対角線が互いに直交することが分かっているので, 二つの対角線の積 ÷ 2 で面積が求まる。
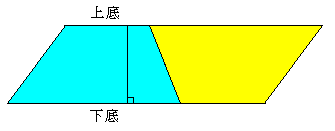
[台形 trapezoid]
一組の対辺が平行な四角形。 図のように, 同じものをくっつけると平行四辺形になるので, (上底 + 下底) × 高さ ÷ 2 で面積が求まる。
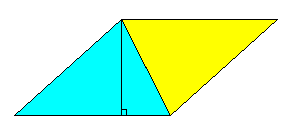
[三角形 triangle]
台形と同様 --- っていうか多分小学校では台形の方が三角形と同様ってやるんだと思った --- に同じものをくっつけると平行四辺形になるので, 底辺 × 高さ ÷ 2.
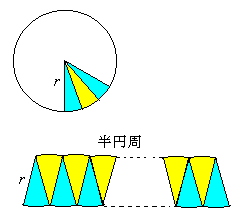
[円板 disk]
これはちゃんと積分を用いて証明すべきことなのだが, 普通は Blaise Pascal (パスカル, 1623 -- 1662) による (?) とかいう --- この部分未確認なので引用しないこと --- 説明によって, 円周率 π を用いて面積が πr2 になる。 その説明は, 図のように, 細かく扇形 sectors に切って並べ替えると半円周が横, 半径が縦の長方形に近付いていくから。