[1]
x = tan θ (-π/2 < θ < π/2) と置くと, x = 0 ⇒ θ = 0, x = 1 ⇒ θ = π/4. 更に dx = dtan θ = dθ/cos2θ = (1 + tan2θ)dθ = (1 + x2)dθ. 即ち dx/(1 + x2) = dθ. 故に
与式 = ∫0π/4dθ = [θ]0π/4 = π/4 - 0 = π/4.
[2]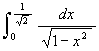 
x = sin θ, -π/2 < θ < π/2 と置くと, x = 0 ⇒ θ = 0,
更に 
従って,
故に,
与式 =∫0π/4dθ = [θ]0π/4 = π/4.
[3] a > 0 とするとき 
.
x = a sin θ, -π/2 < θ < π/2 と置くと, x = 0 ⇒ θ = 0, x = a ⇒ θ = π/2. 更に dx = a cos θdθなので,
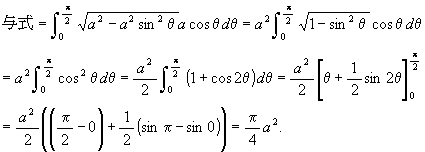
[4]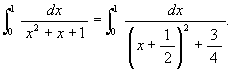 
ここで 
であることを考えて, 
,
-π/2 < θ < π/2 と置く。 すると x = 0 ⇒ θ = π/6, x =
1 ⇒ θ = π/3, 更に 
.
故に
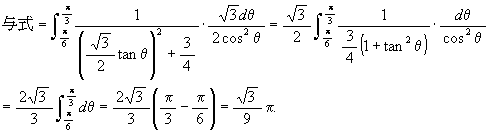
[5] 
先ず 
と置く。 x = 0 ⇒
t = 1, x = 1 ⇒ t = 0 で, t2 = 1 - x より 2tdt = -dx, 即ち
dx = -2tdt. 従って
注) この積分は t = 1 - x と置いても, 又部分積分によっても出来る。
[6] 
と置くと,
.
x = 0 ⇒ t = -1, 
. 更に
故に
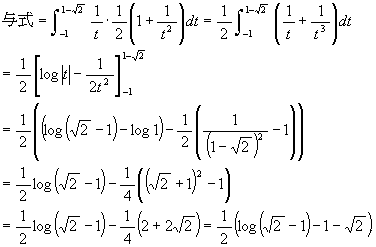
[7] 
と置く。 x = 0 ⇒ θ = 0, x = 1 ⇒ θ = π/4. 
であるから,
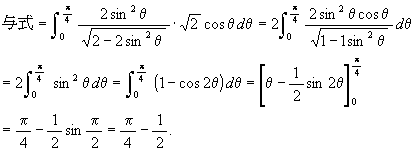
[8]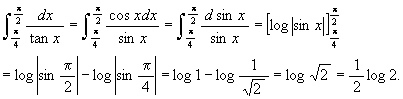 
[9]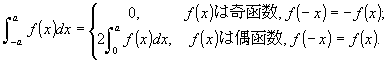 
注) これは公式である。
[証明] 左辺 = ∫0a f(x) dx + ∫-a0 f(x) dx.
第二項で x = -t と置くと,
左辺 = ∫0a f(x) dx + ∫a0
f(-t) (-dt)
= ∫0a f(x) dx + ∫0a f(-t) dt
=∫0a f(x) dx + ∫0a f(-x) dx.
従って, f(x) が奇函数ならば f(-x) = -f(x) であることから,
左辺 = 0;
f(x) が偶函数ならば f(-x) = f(x) であることから, 左辺 = 2∫0a
f(x) dx ■
[10] ∫02a f(x) dx = ∫0a (f(x) + f(x + a)) dx を証明せよ。
[証明] 右辺 = ∫0a f(x) dx + ∫0a f(x + a) dx
第二項で t = x + a と置く。
右辺 =∫0a f(x) dx + ∫a2a
f(t) dt
= ∫0a f(x) dx + ∫a2a f(x) dx =
左辺 ■
[11] ∫0a f(x) dx = ∫0a/2 (f(x) + f(a - x)) dx.
これも [10] 同様に証明できる。