定理 [Pappus (Pappos) of Alexandria]
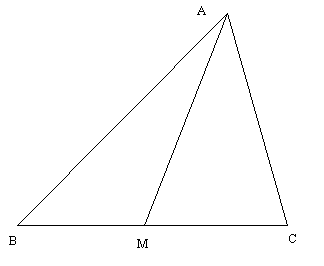
△ABC に於て辺 BC の中点を M とすると
AB2 + AC2 = 2(AM2 + BM2).

通常この定理を Pappus の中線定理 parallelogram theorem という。 欧米でこれを 「平行四辺形の定理」 と呼ぶのは, 良く考えてみれば, この定理が平行四辺形の平行でない二辺の長さと, 対角線の半分の長さの定理に翻訳されることから想像できよう。
先ず vectors を使った証明:
a = MA, b = MB と置く。 AB = b - a, CA = a - (-b) = a + b であるから
AB2 + AC2 = |b - a|2
+ |a + b|2
= |a|2 + 2a・b + |b|2
+ |a|2 - 2a・b + |b|2
= 2(|a|2 + |b|2) = 2(AM2
+ BM2)□
初等的には次のように証明される:
(1)  ∠B
も ∠C も鋭角の時:
∠B
も ∠C も鋭角の時:
頂点 A から辺 BC に垂線を下ろす (右図)。 その足を H とすると, M = H の時は AB = AC だから三平方の定理より明らか。 それ以外の時は対称性から点 H は辺 MC の内点として一般性を失わない。 この時三つの直角三角形 ABH, ACH, AMH に三平方の定理を適用して
AB2 = BH2 + AH2 … (a)
AC2 = CH2 + AH2 … (b)
AM2 = MH2 + AH2 … (c)
ここで (a) + (b) - 2(c) から
AB2 + AC2 -2AM2
= BH2 + CH2 - 2MH2
= BH2 - MH2 + CH2 - MH2
= (BH + MH)(BH - MH) + (CH + MH)(CH - MH)
= (BM + 2MH)BM + CM(CM - 2MH)
= BM2 + 2MH・BM + CM2 - 2CM・MH
= 2BM2.
(2)  ∠B
又は ∠C が直角の時:
∠B
又は ∠C が直角の時:
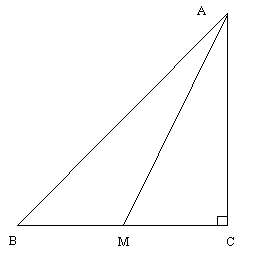
一般性を失わずに ∠C の方が直角であるとして良い。 この時二つの直角三角形 ABC, AMC に三平方の定理を適用して
AB2 + AC2
= 2AC2 + BC2
= 2(AM2 - MC2) + BC2
= 2AM2 + BC2 - 2MC2
= 2AM2 + (2BM)2 - 2MC2
= 2AM2 + 4BM2 - 2BM2
= 2(AM2 + BM2)□
(3) ∠B 又は ∠C が鈍角の時:
一般性を失わずに ∠C の方が鈍角であるとしてよい。

この時, 左図のように辺 BC の延長に降ろした頂点 A からの垂線の足を H とすると,
三つの直角三角形 ABH, ACH, AMH に三平方の定理を適用して
AB2 = BH2 + AH2
AC2 = CH2 + AH2
AM2 = MH2 + AH2
前 (1) と同様にして
AB2 + AC2 -2AM2
= BH2 + CH2 - 2MH2
= BH2 - MH2 + CH2 - MH2
= (BH + MH)(BH - MH) + (CH + MH)(CH - MH)
= (BM + 2MH)BM + (2MH - CM)(-CM)
= BM2 + 2MH・BM + CM2 - 2CM・MH
= 2BM2.□