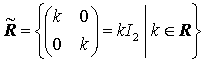 を表すことにする。 すぐ分かるように R̃⊂M2(R)
で, M2(R) は環であるから,
R̃ の元同士には M2(R)
での加法と乗法とを考えることが出来る (勿論結果が R̃
に入るかどうかは分からないが)。
を表すことにする。 すぐ分かるように R̃⊂M2(R)
で, M2(R) は環であるから,
R̃ の元同士には M2(R)
での加法と乗法とを考えることが出来る (勿論結果が R̃
に入るかどうかは分からないが)。R̃ で 集合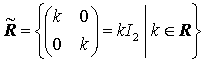 を表すことにする。 すぐ分かるように R̃⊂M2(R)
で, M2(R) は環であるから,
R̃ の元同士には M2(R)
での加法と乗法とを考えることが出来る (勿論結果が R̃
に入るかどうかは分からないが)。
を表すことにする。 すぐ分かるように R̃⊂M2(R)
で, M2(R) は環であるから,
R̃ の元同士には M2(R)
での加法と乗法とを考えることが出来る (勿論結果が R̃
に入るかどうかは分からないが)。
明らかに I2 = 1・I2, 0 = 0・I2 ∈ R̃ であり, 又
kI2 + mI2 = (k + m)I2 ∈
R̃,
(kI2)・(mI2) = (km)I2 ∈
R̃
であるから R̃ は +, ・
で閉じている。 又 kI2 + mI2 = mI2 + kI2 で,
kI2 + 0 = 0 + kI2 = kI2 であるから
R̃ は環, 特に M2(R) の部分環 subring
である。 更に (kI2)・(mI2) = (mI2)・(kI2)
だから可換環であり, k ≠ 0 ならば
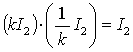 だから R̃ は可換体である。
だから R̃ は可換体である。
よって R̃ をスカラー行列の作る体という。
実は R̃ → R :
kI2 → k は一対一の対応で, 上記によって +, ・ はそのまま R̃
と R で対応がついていることが分かる。 このことは (見かけはともかく) +, ・ という演算についてみれば R̃
と R は全く同じであるということを意味している。 このことを R̃
と R は体として同型 isomorphic であるという。 このことを記号で
![]() と書く。 更に上記の対応 R̃ → R :
kI2 → k のことを R̃
から R への体としての同型写像 isomorphism という。
と書く。 更に上記の対応 R̃ → R :
kI2 → k のことを R̃
から R への体としての同型写像 isomorphism という。
数学に於ては多くの場合, 同型なものを区別しないので, 以下 R̃ も特に区別せずに R と書く。