第一問 (必答 30 点)
[1]
(1) ∀x(x ≧ 0 ⇒ Ax + B > 0) となるためには (graph
を描いてみれば分かるが)
A ≧ 0, B > 0 (各 2 点)
であることが必要十分である。
(2) 式 (1) を x について纏めると
(sin2 α + 2sin α cos α - cos2 α)x + sin2
α - sin α cos α
= (2sin α cos α - (cos2 α - sin2 α))x + (sin2
α - sin α cos α)
= (sin 2α - cos 2α)x + (sin2 α - sin α cos α) > 0.
ここで (1) から
sin 2α - cos 2α ≧ 0, (各 2 点)
sin2 α > sin α cos α. (2 点)
0°≦ α ≦ 180°であるが, sin α ≠ 0
でなければならないので 先ず 0°< α < 180°. この範囲で
sin 2α - cos 2α = (√2)sin(2α - 45°) ≧ 0,
sin α > cos α ⇔ sin α - cos α = (√2)sin(α - 45°) > 0.
0° ≦ 2α - 45°≦ 180°& 0°< α - 45°< 180°- 45°
∴45°≦ 2α ≦ 225°& 45°< α < 180°
45°/2 ≦ α ≦ 225°/2 & 45°< α < 180°
従って 45°< α ≦ 225°/2 (辺々各 3 点).
x の係数を 2α の三角函数に纏めるのが少し難しいかもしれないが, そこは問題を見れば分かるようになっているので, それほど難しくないと思われる。
(1) の問題文が Ax + B を 「x の一次式」 と呼んでいることには問題がある。 余計なことを書かなければよかったのに。
[2] (1) d = log9 x - 3/2 = 0. log9 x = 3/2 だから x = 93/2 = 33 = 27 (2 点)
(2) a = log3 x - 7/2 = 0 とすると x = 37/2 = 33+1/2
= 27√3,
b = log3 x - 5/2 = 0 とすると x = 35/2 = 32+1/2
= 9√3,
c = log9 x - 5/2 = 0 とすると x = 35 = 243.
a < 0, b < 0, c < 0, d < 0 とすると 0 < x < 9√3. (2 点)
二つが正で二つが負という場合は 5/2 < 3 < 7/2 < 5, 3 > 1 より 9√3 < 27 < 27√3 < 243 だから a <0, b > 0, c < 0, d > 0 しか起こらないので 27 < x < 27√3 (辺々各 2 点).
全てが正という場合は 243 < x (2 点).
(3) 常に a < b, c < d は成立している。
a - c = log3 x - 7/2 - log9 x + 5/2 = log3 x
- (log3 x)/(log3 9) - 1
= log3 x - (log3 x)/2 - 1 = (1/2)log3 x - 1.
27 < x < 27√3 だから 1/2 < a - c < 3/4. 即ち a - c > 0. ∴ a > c.
b - d = log3 x - 5/2 - log9 x + 3/2 = (1/2) log3
x - 1. だから同様に
b > d.
a < 0 < d だから
c < a < d < b. (各 1 点)
底の変換公式を知らないと難しいだろうが, あとは場合分けが面倒なだけである。
第二問 (必答 30 点)
(1) 0 ≦ x ≦ 3
⇒ g(x) = ∫0x f(t)dt = ∫0x t dt
= (1/2)x2. (3 点)
x ≧ 3
⇒ g(x) = ∫03 f(t)dt + ∫3x
f(t)dt = 9/2 + ∫3x (-3t + 12) dt
= 9/2 + [-3t2/2 + 12t]03 = 9/2 + (-3x2/2
+ 12x) - (-27/2 + 36)
= 9/2 - 3x2/2 + 12x + 27/2 - 36
= -3x2/2 + 12x - 18 (各 3 点).
(2) 0 < a < 3 とすると g'(a) = a (2 点) だから l
の方程式は
y = a(x - a) + a2/2
y = ax - (1/2)a2 (2 点).
(3) l に於いて y = 0 とすると ax - (1/2)a2 = 0. a
> 0 より x = a/2.
∴Q((1/2)a, 0) (2 点).
-3x2/2 + 12x - 18 = ax - (1/2)a2, x > 3, 0 < a
< 3 と置く。
-3x2 + 24x - 36 = 2ax - a2.
3x2 + 2(a - 12)x - a2 + 36 = 0.
3x2 + 2(a - 12)x - (a2 - 36) = 0.
3x2 + 2(a - 12)x - (a - 6)(a + 6) = 0.
(3x - a - 6)(x + a - 6) = 0.
x = (a + 6)/3, -a + 6.
0 < a < 3 なので 2 < (a + 6)/3 < 3, 3 < 6 - a < 6
であるから x = 6 - a. このとき y = a(6 - a) - a2/2 = 6a -
(3/2)a2 なので
R(6 - a, 6a - (3/2)a2) (x 座標 4 点, y
座標 3 点).
(4) 0 < a < 3 では 6a - (3/2)a2 > 0 である。
そこで
S = △QRH = (1/2)((6 - a) - a/2)(6a - (3/2)a2) = (1/2)a((3/2)a - 6)2
= (1/2)a(9a2/4 - 18a + 36) = (9/8)a3 - 9a2
+ 18a. (4 点)
dS/da = 27a2/8 - 18a + 18 = (9/8)(3a2 - 16a + 16) = (9/8)(3a - 4)(a - 4), 0 < a < 3.
| a | (0) | 4/3 | (3) | ||
| dS/da | (18) | + | 0 | - | (-45/8) |
| S | 0 | ↑ | 最大 32/3 |
↓ | (27/4) |
従って S は a = 4/3 (4 点) の時最大値 32/3 を採る。
場合分けや check が面倒なだけで普通である。
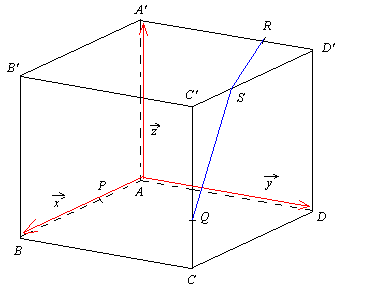
第三問 (選択 20 点)
本問では vectors はすべて太字斜体を用いる。

AP = ax,
AQ = AC + CA = x +
y + az,
AR = AA' + A'R = z + (1
- a)y.
(1) PQ = AQ - AP = x
+ y + az - ax
= (1 - a)x + y + az.
(全部で 2 点)
PR = AR - AP = (1 - a)y
+ z - ax
= -ax + (1 - a)y + z. (2 点)
PQ : PR = √((1 - a)2 + 1 + a2) : √(a2 + (1 -
a)2 + 1)
= 1: 1 (1 点).
PQ2 = (1 - a)2 + 1 + a2 = 2a2 -
2a + 2
= 2(a2 - a + 1) (2 点).
PQ・PR = ((1 - a)x + y
+ az)・(-ax + (1 - a)y + z)
= -a(1 - a) + (1 - a) + a
= -a + a2 + 1 - a + a
= a2 - a + 1 (1 点).
0 < ∠QPR < 180° で
a2 - a + 1 = 2(a2 - a + 1) cos ∠QPR
cos ∠QPR = 1/2 より ∠QPR = 60°(2 点).
(2) AG = AP + PG = AP
+ (1/3)(PQ + PR)
= ax + (1/3)((1 - 2a)x + (2 - a)y + (a
+ 1)z)
= (1/3)((a + 1)x + (2 - a)y + (a + 1)z).
DG = AG - AD = (1/3)((a + 1)x
+ (2 - a)y + (a + 1)z) - y
= (1/3)((a + 1)x - (a + 1)y + (a + 1)z)
= ((a + 1)/3)(x - y + z).
(2 点)
AC' = x + y + z.
C'S = kC'D' = -kx, 0 < k < 1 と置く。
AS = (1 - k)x + y + z,
SQ = AQ - AS = kx + (a -
1)z,
SR = AR - AS = (k - 1)x
- ay.
SQ2 = SR2 より
k2 + (a - 1)2 = (k - 1)2 + a2
k2 + a2 - 2a + 1 = k2 - 2k + 1 + a2
∴k = a. (2 点)
SD = AD - AS
= (a - 1)x - z. (2 点)
(3) SG・DG = (AG - AS)・DG
= (1/3)(2(2a - 1)x - (a + 1)y + (a - 2)z)・((a + 1)/3)(x - y + z)
= ((a + 1)/9)(4a - 2 + a + 1 + a - 2)
= ((a + 1)/9)(6a - 3) = 0
だから a = 1/2 (2 点).
0 < ∠QSR < 180°で
cos ∠QSR = SQ・SR/(SQ・SR) = a(a - 1)/√((a2
+ (a - 1)2)((a - 1)2 + a2))
= a(a - 1)/(2a2 - 2a + 1) = (1/2)・(-1/2)/(1/2 - 1 + 1) = -1/2.
よって ∠QSR = 120°(2 点).
図をちゃんと描ければ基本通り。
SQ2 = SR2 に関しては正解が分かってから図を正確に書いてみると, 合同な三角形が出来ていることが分かる。 又 (3) では S, Q, R を通る平面で切ると, 切り口が正六角形になっていることは中学生で (a = 1/2 の場合だけかもしれないが) 勉強していると思われる。
第四問 (選択 20 点)
(1) |z0|2 = 4×1 = 4. ∴|z0| = 2 (2 点).
arg z0 ≡ arg ((√3) + i) + arg(cos θ + i sin θ) = 30°+ θ (mod 360°). (2 点)
(2) z1 = 4((1 - sin θ) + i cos θ)2/((1 - sin θ)2
+ cos2 θ)
= 4(1 - 2sin θ + sin2θ - cos2θ + 2i(1 - sin θ)cos θ)/(2 -
2sin θ)
= 2(1 - 2sin θ + 2sin2θ - 1+ 2i(1 - sin θ)cos θ)/(1 - sin θ)
= 2(-2sin θ(1 - sin θ) + 2i(1 - sin θ)cos θ)/(1 - sin θ)
= 4(-sin θ + i cos θ) (2 点)
= 4(cos(90°+ θ) + i sin(90°+ θ)).
∴|z1| = 4, arg z1 = 90°+ θ (各 2 点).
(3) |z1/z0| = 4/2 = 2 (1 点).
arg(z1/z0) ≡ arg z1 - arg z0 = (90°+
θ) - (30°+ θ) = 60°(mod 360°). (1 点)
よって △OP0P1 は OP1 が斜辺の直角三角形になるので P0P1
= 2√3. (2 点)
(4) (3) で言ったように ∠OP0P1 = 90°. 従って ∠OP2P1
= ∠OP0P1 = 90°(円周角).
arg z2 = arg(-2/z1) ≡ arg(-2) - arg z1 = 180° -
(90°+ θ) = 90°- θ
であるから向きを考えて
arg ((z1 - z2)/(-z2)) = -90° (2 点).
(z1 - z2)/(-z2) = -z1/z2
+ 1 = z1/(2/z1) + 1 = z12/2 + 1
= 8(-cos 2θ - i sin 2θ) + 1
= -8cos 2θ + 1 - 8i sin 2θ ∈ iR (純虚数)
だから
8 cos 2θ - 1 = 0. (2 点)
8(1 - 2sin2θ) - 1 = 0
7 - 16sin2θ = 0.
sin2θ = 7/16
0 < θ < 90°より
sin θ = (√7)/4 (2 点).
(4) は真面目に考えると arg < 0 になることを言うのが面倒だが, 問題に書いてあるからそのままやればよい。 図を描いてみると少し分かるかも。
1998 年に三重大学と岡山大学 (理系) で類題が出ているというので調べさせていただいた。 こちらに載せる。
第五問 (選択 20 点)
(1) E(X) = (1/8)Σk=18k = (1/8)×(1/2)×8×9 = 9/2.
(2 点)
V(X) = E(X2) - E(X)2 = (1/8)Σk=18k2
- (9/2)2 = (1/8)×(1/6)×8×9×17 - 81/4
= 51/2 - 81/4 = (102 - 81)/4 = 21/4 (2 点).
(2) E(Y) = E(pX + q - 100) = pE(X) + q - 100 = (9/2)p + q - 100 (3 点).
(3) p は偶数でなければならないから p' を正の整数として p = 2p' と置く。 即ち
9p' + q = 100
q = 100 - p' > 0 より 9p' < 100
p' < 100/9 = 11 + 1/9.
だから p' が 11 個適合する。 従って 11 組で (2 点)
p' の最小値は 1 で最大値は 11, 即ち
p (= 2p') の最小値は 2 で最大値は 22. (各 2 点)
(4) V(Y) = p2V(X) = (21/4)p2. (3 点)
よって N = 0 の時 C = min V(Y) は p = 2 の時で C = 21. (各 2 点)
極普通の問題
第六問 (選択 20 点)
| 100 | S の座標の入力 | |
| 110 | Rの y 座標の入力 | |
| 120 | PS2 を計算 | |
| 130 | QS2 を計算 | |
| 140 | RS2 を計算 | |
| 150 | D = P とする | |
| 160 | E = Q とする | |
| 170 | F = R とする | |
| 180 | D < E だったら D と E の入れ替え。結果: E ≦D | |
| 190 | E < F だったら E と F の入れ替え。結果: F ≦ E. | |
| 注意: P と R は比較されていないことがある。 以下略 |
(1) 上記のようなので ア: 0, イ: 3. (各 2 点)
(2) ウ: 5. (2 点)
(3) 三点 P, Q, R が全て出力されるということは PS2 = QS2 = RS2
ということだから
P = (5 - 2)2 + 42 = 32 + 42 = 25,
Q = (5 - 9)2 + (4 - 7)2 = 42 + 32 =
25,
∴R = (5 - 8)2 + (4 - a)2 = 25.
(4 - a)2 = 16
a - 4 = ±4
a = 4 ± 4
∴ a = 8 又は 0 (2 点)
(4) 要するに 180 行から M を最小値 (F) として用いたいのである。
カ: 1, キ: 2. (各 2 点)
(5) 実際にやってみると良い
0: 180 行目で F < E となるが 190 で E < D となるので最大値が D になってしまう。
1: 例えば最初 P < Q < R としてみると D = Q, E = R, F = P となって最大値が E ところが最初 Q < R < P としてみると
E = Q, R = F, D = P のままで最大値が D となるからこれではまずい。
2: 最大と最小というのは順序関係が逆になっているだけなのだから, これで上手くいくはずである。
3: 1 と同様のことが起こる。 R < Q < P のときも上手くいかない。
だから 2. (2 点)
(6) F が最小にはなっているので, あとは D と E を大きさの順に並べればよい。 そのためにはもう一度比較すればよいので ケ: 2
(2 点)
最小値は F だから コ: 5 (2 点).
最大値は F ≦ E ≦ D としているので サ: 3 (2 点).
自分が computer になったつもりになって順に実行してみればよい。 Swap の program を組んだことがない人にとってはア,イが難しかったかもしれない。 何故他のが駄目なのかまで考えると (5) は難しいが, 正解はどれか一つしかないのでそれほど難しくはないであろう。
問題とは関係ないが (6) で 「あとは点を出力する 200 行目以降の部分を修正するだけでよい」 ってそれが大変なんだろ, って思ったのは僕だけではないはず。
センター試験の目次に戻る。