第一問 (必答 30 点)
[1] t = sin θ より, 二倍角の公式から
cos 2θ = cos2θ - sin2θ = 1 - 2sin2θ
= 1 - 2t2. (2 点)
∴f(θ) = 3(1 - 2t2) + 4t
= -6t2 + 4t + 3 (2 点)
= -6(t2 - (2/3)t) + 3
= -6((t - 1/3)2 - 1/9) + 3
= -6(t - 1/3)2 + 2/3 + 3
= -6(t - 1/3)2 + 11/3.
0 ≦ t ≦ 1 より
最大値 11/3 (t = 1/3) (3 点),
最小値 1 (t = 1) (3 点)
である。
f(α) = 3 とすると
-6t2 + 4t = 0.
3t2 - 2t = 0
t(3t - 2) = 0.
t = 0, 2/3.
即ち sin α = 0, 2/3.
0°< α < 90°なので 0 < sin α < 1 だから sin α = 2/3.
従って cos α = √(1 - sin2α) = (√5)/3.
従って
sin(α + 30°)
= sin α cos 30°+ cos α sin 30°
= (2/3)((√3)/2) + ((√5)/3)(1/2)
= (2(√3) + √5)/6. (5 点)
ちゃんと書くと大変だが, 誘導に従って解けばそれほど難しくない。
[2]
(1) 底の条件 x > 0 & x ≠ 1. (各 1 点)
底の変換公式により
logx27 = (log327)/log3x = 3/log3x.
(2 点)
(2) 従って 2log3x - 12/log3x ≦ 5.
log3x < 0 つまり 0 < x < 1 の時
2(log3x)2 - 5log3x - 12 ≧
0. (3 点)
であり log3x > 0 つまり x > 1 の時
2(log3x)2 - 5log3x - 12 ≦ 0
となる。
最初の場合
(2log3x + 3)(log3x - 4) ≧ 0
より log3x ≦ -3/2, 4 ≦ log3x.
log3x < 0 だったから log3x ≦ -3/2.
底 3 > 1 より x ≦ 3-3/2 = 1/√33 = 1/(3√3) = (√3)/9.
二番目の場合, 同様にして,
-3/2 ≦ log3x ≦ 4
で
log3x > 0 であったから 0 < log3x ≦ 4.
底 3 > 1 より 1 < x ≦ 34 = 81.
以上より 0 < x ≦ (√3)/9, 1 < x ≦ 81. (各 4 点)
これも誘導に沿って解いていけば難しくない。
標準的な問題。
第二問 (必答 30 点)
(1) C1 で y' = 2x. y'x=t = 2t より接線は
y = 2t(x - t) + t2.
y = 2tx - t2. (各 2 点)
これを C2 に代入すると
2tx - t2 = x2 - 4ax + 4a(a + 1)
x2 - 2(2a + t)x + 4a2 + 4a + t2 = 0.
接するので x に関する判別式を採ると
D/4 = (2a + t)2 - (4a2 + 4a + t2)
= 4at - 4a = 4a(t - 1) = 0.
a > 0 より t = 1. (5 点).
代入して, 接線は y = 2t - 1. (2 点)
さて, t = 1 の時,
x2 - 2(2a + 1)x + 4a2 + 4a + 1 = 0.
x2 - 2(2a + 1)x + (2a + 1)2 = 0.
(x - (2a + 1))2 = 0.
∴x = 2a + 1.
これを接線の式に代入して
y = 2(2a + 1) - 1 = 4a + 1.
よって接点は (2a + 1, 4a + 1). (x 座標が 3 点, y 座標が 2 点)
(2) x2 = x2 - 4ax + 4a(a + 1) と置くと
4ax = 4a(a + 1).
a > 0 より x = a + 1. (2 点)
よって P(a + 1, (a + 1)2).
m: y = 2(x - (a + 1)) + (a + 1)2
= 2x - 2a - 2 + a2 + 2a + 1
= 2x + a2 - 1. (3 点)
y 切片: a2 - 1 > 0 と置くと a > 0 より a > 1. (3 点)
この時, m と C1 の交点で x > 0 のものの x 座標は
x2 = 2x + a2 - 1
x2 - 2x + 1 = a2.
(x - 1)2 = a2.
x = 1 ± a.
a > 1, x > 0 より x = a + 1.
よって
S = ∫0a+1(2x + a2 - 1 - x2)dx
= [x2 + (a2 - 1)x - (1/3)x3]0a+1
= (a + 1)2 + (a - 1)(a + 1)2 - (1/3)(a + 1)3
= (1/3)(a + 1)2(3 + 3(a - 1) - (a + 1))
= (1/3)(a + 1)2(2a - 1). (係数 1/3 は
2 点, 残り 4 点)
微分・積分の問題としては非常に簡単な問題。
第三問 (選択 (新・旧) 20 点)
(1) 2b = a + c, a2 = bc なので
c = 2b - a を二番目の式に代入して
a2 = b(2b - a)
a2 + ab - 2b2 = 0
(a - b)(a + 2b) = 0.
a ≠ b より a = -2b. 即ち b = (-1/2)a. (3 点)
c = 2b - a = -a - a = -2a. (3 点)
相異なるので a ≠ 0 である。
公差は b - a = (-1/2)a - a = (-3/2)a. (2 点)
(2) -2a, a, (-1/2)a (a ≠ 0) が等比数列だから, 公比は -1/2.
従って
Σn=18yn = (-2a(1 - (-1/2)8))/(1 -
(-1/2)) = (-2a(1 - 1/256))/(1 + 1/2)
= (2/3)・(-2)・(255/256)a = (-85/64)a. (4 点)
(3) b, c, a という数列は (-1/2)a, -2a, a で
w1 = -2a - (-1/2)a = ((-4 + 1)/2)a = (-3/2)a,
w2 = a - (-2a) = 3a.
公差は w2 - w1 = 3a - (-3/2)a = ((6 + 3)/2)a = (9/2)a.
(2 点)
従って
wn = (-3/2)a + (n - 1)(9/2)a
= (-3/2)a - (9/2)a + (9/2)n・a
= (-12/2)a + (9n/2)a = ((9n - 12)/2)a. (2 点)
よって
zn = Σk=1n-1 wk
= (-1/2)a + a((9/2)・(1/2)n(n - 1) - 6(n - 1))
= (-1/2)a + a(9n(n - 2)/4 - 6(n - 1))
= (a/4)(-2 + 9n2 - 9n - 24n + 24)
= (a/4)(9n2 - 33n + 22). (4 点)
極めて基本的。
第四問 (選択 (新・旧) 20 点)
本問では vectors はすべて太字斜体を用いる。
(1) |a + b|2 = 1
|a|2 + |b|2 + 2a・b
= 1
1 + 1 + 2a・b = 1
故に a・b = -1/2. (3 点)
|2a + b|2 = 4|a|2 +
4a・b + |b|2 = 4 - 2 +
1 = 3 なので
|2a + b| = √3. (3 点)
(2a + b)・b = 2a・b + |b|2 = -1 + 1 = 0 より, 2a + b と b の成す角は 90°. (3 点)
(2) c = ma + nb と置くと
a⊥c より a・c = m|a|2
+ na・b = m - (1/2)n = 0 故に n = 2m.
|c|2 = m2 + n2 + 2mn・(-1/2) =
1
m2 + n2 - mn = 1
m2 + 4m2 -2m2 = 1.
3m2 = 1.
m = ±(√3)/3.
ここで
b・c = ma・b + n|b|2
= -m/2 + n > 0 即ち m < 2n = 4mなので m > 0 で
m = (√3)/3.
故に
c = m(a + 2b) = ((√3)/3)(a +
2b) (3 点)
(3) p = xa + yc
= (x + y/√3)a + (2y/√3)b.
従って p・a = x + (y/√3) - (1/2)(2y/√3) = x だから
0 ≦ x ≦ 1. (各 1 点)
又 p・b = (-1/2)(x + y/√3) + (2y/√3)
= (-1/2)x + (3/(2√3))y
= (-1/2)x + ((√3)/2)y.
従って 0 ≦ (-1/2)x + ((√3)/2)y ≦ 1.
0 ≦ -x + (√3)y ≦ 2.
x ≦ (√3)y ≦ x + 2. (各 1 点)
p・c = (xa + yc)・c
= xa・c + y = y.
だから y ≦ (x + 2)/√3 ≦ 3/√3 = √3 が最大値。 (2 点)
このとき x = 1, y = √3 だから
p = 2a + 2b. (2 点)
これも極めて基本的な問題。
第五問 (選択 (新・旧) 20 点)
[1] (1)`x
= (3 + 4 + 5 + 4 + 4) = 4 + (-1 + 0 + 1 + 0 + 0)/3 = 4.
x2 の平均 = (9 + 16 + 25 + 16 + 16)/5 = 16 + (-7 + 0 + 9 + 0 + 0)/5 =
16+ 2/5 = 16.4.
よって x の分散 = 16.4 - 42 = 16.4 - 16 = 0.4. (2 点)
(2)`y = (7 + 9 + 10 + 8 +6)/5 = 8 なので, t = y - 8. (2 点)
(3) y2 の平均 = 64 + (1 + 1 + 4 + 4)/5 = 64 + 10/5 = 64 + 2 = 66.
y の分散 = 66 - 82 = 66 - 64 = 2.
よって √(0.4/2) = √((1/2)・(2/5)) = √(1/5) = 1/√5 = (√5)/5. (3 点).
(4) r = (1/5)Σ [((x -`x)/√0.4)・((y -`y)/√2)]
= (1/(2√5))・(-1・(-1) + 0・1 + 1・2 + 0・0 + 0・(-2))
= (1/(2√5))・(1 + 2) = 3/(2√5)).
故に r2 = 9/20 = 45/100 = 0.45. (3 点)
r' = (1/5)Σ [((x -`x)/√0.4)・((1/√5)(y -`y)/√2)]
= r = 3/(2√5))
従って (r')2 = 0.45. (3 点)
こちらの問題は極めて普通である。 ところが...
[2] (1) (2) の相関表より, 資料の総数は 50 で
| 代表値 | 10 | 30 | 50 | 70 | 90 |
| p | 4 | 13 | 4 | 24 | 5 |
| q | 4 | 10 | 15 | 16 | 5 |
従って
`p = 50 + (-4・4 + (-2)・13 + 2・24 + 4・5)・10/50 = 50 + (-16 - 26 + 48 +
20)/5 = 50 + 26/5
= 55.2.
p2 の平均 = 2500 + (1600・(4 + 5) + 400・(13 + 24))/50 = 3084.
p の分散 = 3048 - 55.22 = 0.96.
`q = 50 + (-4・4 + (-2)・10 + 2・16 + 4・5)/5 = 50 + (-16
- 20 + 32 + 20)/5 = 50 + 16/5
= 53.2.
q2 の平均 = 2500 + (1600・(4 + 5) + 400・(10 + 16))/50 = 2996.
q の分散 = 2996 - 53.22 = 165.76
相関係数 = (1/50)Σ[((p -`p)/√0.96)((q -`q)/√165.76)]
= … = -0.58568
≒ -0.6 なので 2. (3 点)
(2) 上の表より見比べて p の方は 4 (2 点), q の方は 5 (2 点)
こちらの問題は, 見たとたんに嫌になった。
実際には (2) から解いたし, 相関係数の計算は MS Excel を使ってしまった。
実際, 相関係数はもっと簡単に求まるんだろうか?
それとも, まあ負の相関は直ぐに分かるから, このくらいの分布だとこのくらいの数値だとか言ってやるのだろうか? よく分からないが,
正攻法でやると時間ばかりかかって良い問題とは言えない。
が, 予備校の問題分析を見ると 「易しい」 と書いてある。 この辺良く分からない。
(1) の問題が簡単だという人のご教示を願いたい。
200/61/28 追記:
相関係数 c は -1 ≦ c ≦ 1 の範囲しか取らないので 0 と 6 は論外ということが分かる。 証明は Cauchy-Schwarz の不等式による。 又ここによればこの不の相関はかなり強い。
が, 見る人が見れば -0.9 もないということが分かるのではないか。
MS Excel で実験的に相関係数 -0.9 のものを作ってみた。 File はこれ (Excel
2003 SP2 で作成)。 各点をドラッグして動かしてみることが出来るので, 動かすと, どう相関係数が変わるかを実験してみて欲しい。
これを見ると, 相関係数 -0.9 ではないなという気がする。
第六問 (選択 (新・旧) 20 点)
(1) INT は切り捨てるから 4. (2 点)
(2) 割り切れないときには因数の候補を段々大きくしていかなくてはならないので イウエ は 120. (3 点)
N = 1 ということは, 既に全ての素因数を見つけてしまっているので オカキ は 230. (3 点)
(3) 60 = 22・3・5 = 2・2・3・5 だから
160 行は 4 回 (2 点).
180 行は (60 に限らず) 何にせよ 1 回だけ。 (2 点)
61 は素数なので, 160 行も 1 回 (2 点), 180 行も 1 回 (1 点)。
(4) 素因数で割るので 0. (3 点),
割り切れる限り割ってしまうので スセソ は 161. (2 点)
Program としてもまあ普通で, 以前よりは良い問題になったと思う。
いつもと同じように, 自分が computer になったつもりで, 一行々々実行していけば分かるはず。
第七問 (選択 (旧) 20 点)

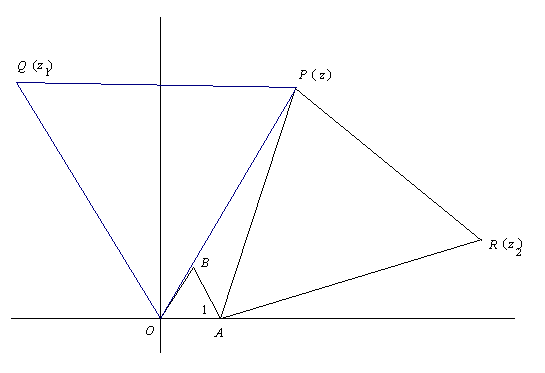
(1) β = (1 + (√3)i)/2. (2 点)
Q は P を O の周りに 60°回転した点 (2 点) なので
z1 = βz なので 0. (2 点)
R は P を O に平行移動してから A を60°回転させて, 今度は O を P 迄平行移動させると得られるから z2 = β(1 - z) + z なので 0. (2 点).
従って
w = (z1 - β)/(z2 - β) = (βz - β)/(β(1 - z) + z - β) = β(z
- 1)/(β - βz + z - β)
= (β/(1 - β))・((z - 1)/z) = ((1 + (√3)i)/2)・(2/(1 - (√3)i))・((z - 1)/z)
= ((1 + (√3)i)2/(1 + 3))・((z - 1)/z) = ((-2 + 2(√3)i)/4)・((z - 1)/z)
= ((-1 + (√3)i)/2)・((z - 1)/z). (4 点)
(2) BQ⊥BR ⇔ w ∈ iR*.
((-1 + (√3)i)/2)・((z - 1)/z) ∈ iR*.
以下 z ̄ で z の共役複素数を表す。 このとき
-[((-1 + (√3)i)/2)・((z - 1)/z)] ̄ = ((-1 + (√3)i)/2)・((z - 1)/z).
((1 + (√3)i)/2)・((`z - 1)/`z)
= ((-1 + (√3)i)/2)・((z - 1)/z).
(1 + (√3)i)・((`z - 1)/`z)
= (-1 + (√3)i)・((z - 1)/z).
(1 + (√3)i)(`z - 1)z = (-1 + (√3)i)(z - 1)`z.
(1 + (√3)i)`zz - (1 + (√3)i)z = (-1 + (√3)i)`zz
- (-1 + (√3)i)
(1 + (√3)i + (1 - (√3)i)`zz - (1 + (√3)i)z - (1 -
(√3)i)`z = 0.
2`zz - (1 - (√3)i) ̄z - (1 - (√3)i)`z
= 0.
`zz - ((1 - (√3)i)/2) ̄z - ((1 - (√3)i)/2)`z
+ ((1 - (√3)i)/2) ̄・((1 - (√3)i)/2) = 1.
|z - ((1 - (√3)i)/2)|2 = 1.
従って 中心が (1 - (√3)i)/2 (5 点), 半径が 1. (3 点)
共役複素数の処理に慣れていないと最後が一寸難しいかも。
第八問 (選択 (旧) 20 点)
(1) Y = 4 ということは, Zi のどれか一つが 4, 残りは全て 0 ということで, つまり四回共同じ数が出るのだから
6・(1/6)4 = 1/63 = 1/216. (3 点)
(2) Y = 2 ということは, 或る Zi = 2 で, 残りは Zk = 2, 3, 又は 4 でなければならないが ΣZi = 4 であるから, Zk = 2. つまり 二つの Zi = Zk = 2 で残りは 0.
(どの二回が)・(どの二つ)
4C2・6C2(1/6)4 = 5/72.
(3 点)
(3) Y = 3 ということはあり得ない。 Y = 1 はありうるので k = 1, 2, 4 の 3 個。 (2 点)
Y = 1 は Y = 2, 4 の余事象だから
1 - (1/216 + 5/72) = 1 - 16/216 = 25/27. (3 点)
平均は 25/27 + 2・5/72 + 4・1/216 = (100 + 15 + 2)/108 = 117/108 = 13/12.
(3 点)
Y2 の平均は 25/27 + 4・5/72 + 16・1/216 = (50 + 15 + 4)/54 = 69/54 = 23/18.
よって分散は 23/18 - (13/12)2 = (184 - 169)/144 = 15/144 = 5/48.
(3 点)
(4) X ≧ 2 でない場合は, X = 1 しかない。 それは全て一回ずつということだから
64 - 6P4 = 6・6・6・6 - 6・5・4・3 = 6・(6・6・6 -
5・4・3) = 6・(6・6・6 - 5・2・6)
= 6・6・(6・6 - 5・2) = 6・6・2・(3・6 - 5) = 6・6・2・(18 - 5) = 6・6・2・13.
一方 Y = 1 の場合は 「1 が四つ」 か 「1 が二つで, もう一個は 2」 か 「1 と 3」 のどれかだが, 「1 が四つ」 は X ≧ 2 ではない。
Y = 1 の確率からして, その場合は 64・25/27 = 6・23・52.
これから 6P4 を引いたのが 「X ≧ 2 で且つ Y = 1 の場合」 の数だから
6・23・52 - 6・5・4・3 = 6・5・(23・5 - 4・3) =
6・5・4・(2・5 - 3) = 6・5・4・7.
従って求める確率は
6・5・4・7/(6・6・2・13) = 35/39. (3 点)
(3), (4) は余事象に気付かないと大変。
因みに 「1 が二つで, もう一個は 2」 の場合の数は
(どの一つが 2 になるか)・(どの目が対象か)・(四回中どの二回か)・(その順序)
= 3・6C3・4C2・2!
であり, 「1 と 3」 の場合の数は
(どっちが 3 か)・(どの一回が 1 か)・(どの目か) = 2・4・6C2 となる。
センター試験の目次に戻る。