2008 年数学 II ・ B 問題

Sunday, 20th January, 2008.
13:30 -- 14:30 (1hr)
平均 51.01

注:

第一問, 第二問は必答。
第三問から第六問のうちから二問選択。
計四問を解答。

第一問 (必答 30 点)

[1] 実数 x, y は
1 = 3^1+log₁₀x - 5^y ……………… (*)
を満たしている。 このとき
K = 5^y/3 + 3^-log₁₀x
の最小値を求めよう。

真数の条件により x > [ ア ] である。 但し, 対数 log_ab に対し, a を底といい, b を真数という。 次に (*) より
5^y = [ イ ]・3^log₁₀x - 1
である。 z = 3^log₁₀x と置くと, 5^y > 0 であるから, z のとり得る値の範囲は
z > [ ウ ]/[ エ ]
となる。 更に
K = z + [ オ ]/z - 1/[ カ ]
となるから, K は z = [ キ ] のとき, 最小値 [ ク ]/[ ケ ] をとる。 このとき x = [ コ ], y = log_{[ サ ]}[ シ ] である。

[2] a を正の定数とする。 点 O を原点とする座標平面において, 中心が O で, 半径が 1 の円と半径が 2 の円をそれぞれ C₁, C₂ とする。 θ ≧ 0 を満たす実数 θ に対して, 角 aθ の動径と C₁ の交点を P とし, 角 π/2 - θ/3 の動径と C₂ との交点を Q とする。 ここで, 動径は O を中心とし, その始線は x 軸の正の部分とする。

(1) θ = π のとき, Q の座標は(√[ ス ], [ セ ]) である。

(2) 三点 O, P, Q がこの順に一直線上にあるような最小の θ の値は
([ ソ ]/([ タ ]a + [ チ ]))π
である。 θ が
0 ≦ θ ≦ ([ ソ ]/([ タ ]a + [ チ ]))π
の範囲を動くとき, 円 C₂ において点 Q の軌跡を弧とする扇 (おうぎ) 形の面積は
([ ツ ]/([ テ ]a + [ ト ]))π
である。

(3) 線分 PQ の長さの自乗 PQ² は
[ ナ ] - [ ニ ]sin(([ ヌ ]a + [ ネ ])/[ ノ ])θ)
である。

(4) x の函数 f(x) を
f(x) = [ ナ ] - [ ニ ]sin(([ ヌ ]a + [ ネ ])/[ ノ ])x)
とおき, f(x) の正の周期のうち最小のものが 4 π であるとすると,
a = [ ハ ]/[ ヒ ] である。

第二問 (必答 30 点)

a を正の実数とし, x の二次函数 f(x), g(x) を
f(x) = (1/8)x²
g(x) = -x² + 3ax - 2a²
とする。 又, 放物線 y = f(x) 及び y = g(x) をそれぞれ C₁, C₂ とする。

(1) C₁ と C₂ の共有点を P とすると, 点 P の座標は (([ ア ]/[ イ ])a, ([ ウ ]/[ エ ])a²) である。 又, 点 P における C₁ の接線の方程式は
y = ([ オ ]/[ カ ])ax - ([ キ ]/[ ク ])a²
である。

(2) C₁ と x 軸及び直線 x = 2 で囲まれた図形の面積は, [ ケ ]/[ コ ] である。 又, C₂ と x 軸の交点の x 座標は [ サ ], [ シス ] であり, C₂ と x 軸で囲まれた図形の面積は ([ セ ]/[ ソ ])a³ である。

(3) 0 ≦ x ≦ 2 の範囲で, 二つの放物線 C₁, C₂ と二直線 x = 0, x = 2 で囲まれた図形を R とする。 R の中で, y ≧ 0 を満たす全ての部分の面積 S(a) は
0 < a ≦ [ タ ] のとき S(a) = -([ セ ]/[ ソ ])a³ + [ ケ ]/[ コ ]
[ タ ] < a ≦ [ チ ] のとき S(a) = -([ ツ ]/[ テ ])a³ + [ ト ]a² - [ ナ ]a + [ ニ ]
[ チ ] < a のとき S(a) = [ ケ ]/[ コ ]
である。 従って, a が a > 0 の範囲を動くとき, S(a) は a = [ ヌ ]/[ ネ ] で最小値 [ ノ ]/[ ハヒ ] をとる。

第三問 (選択 20 点)

(1) 数列 {a_n} は初項が 7, 公差が -4 の等差数列とする。 数列 {a_n} の一般項は
a_n = [ アイ ]n + [ ウエ ]
であり, 初項から第 n 項までの和は
Σ_k=1ⁿa_k = [ オカ ]n² + [ キ ]n
である。

(2) 数列 {b_n} は, 第 n 項が
b_n = pn² - qn - r
という n の二次式で表され
b_n+1 - 2b_n = [ オカ ]n² + [ キ ]n (n = 1, 2, 3,...) …… (1)
を満たすとする。 このとき
p = [ ク ], q = [ ケ ], r = [ コ ]
であり, b₁ = [ サシ ] である。

更に, 次の条件によって定まる数列 {c_n} を考えよう。
c₁ = 1,
c_n+1 - 2c_n = [ オカ ]n² + [ キ ]n (n = 1, 2, 3,...) …… (2)
式 (1) と式 (2) より, d_n = c_n - b_n と置くと
d_n+1 - [ ス ]d_n = 0
が成り立つ。 これより, 数列 {c_n} の一般項は
c_n = [ セ ]・[ ソ ]^n-1 + [ ク ]n² - [ ケ ]n - [ コ ]
である。
数列 {c_n} の初項から第 n 項までの和 Σ_k=1ⁿc_k は
[ タ ]・[ チ ]ⁿ + ([ ツ ]/[ テ ])n³ - ([ ト ]/[ ナ ])n² - ([ ニヌ ]/[ ネ ])n - [ ノ ]
となる。

第四問 (選択 20 点)

本問では vectors はすべて太字斜体を用いる。

四面体 OABC において, OA = OB = BC = √2, OC = CA = AB = √3 である。 a = OA, b = OB, c = OC と置く。

(1) |a - b|² = [ ア ] であり, a・b = [ イ ]/[ ウ ] である。
又, b・c = [ エ ]/[ オ ], c・a = [ カ ] である。

(2) 直線 AB 上の点 P を CP・a = 0 であるようにとると
CP = ([ キ ]/[ ク ])a + ([ ケ ]/[ コ ])b - c
となり, 点 P は線分 AB を 1: ([ サ ]/[ シ ]) に内分する。 又, CP・b = [ ス ] であり, |CP| = (√[ セソ ])/[ タ ] である。

CP は三角形 [ チ ] の各辺と垂直であるから, 直線 CP は三角形 [ チ ] を含む平面に垂直である。 但し [ チ ] については, 当てはまるものを, 次の 0 〜 3 のうちから一つ選べ。

0 ABC, 1 OBC, 2 OAC, 3 OAB.

三角形 [ チ ] の面積は (√[ ツテ ])/[ ト ] であるから, 四面体 OABC の体積は [ ナ ]/[ ニヌ ] である。

第五問 (選択 20 点)

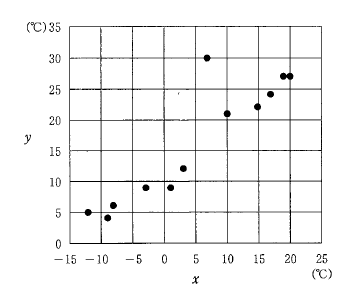
ある都市におけるある年の月毎の最低気温を変数 x, 最高気温を変数 y とする。 但し, 単位は ℃ とし, 最低気温と最高気温は, 一日の最低気温と最高気温について月毎に平均をとり, 小数第一位を四捨五入したものとする。

次の図は変数 x と変数 y の相関図 (散布図) である。

以下, 小数の形で解答する場合は, 指定された桁 (けた) 数の 一つ下の桁を四捨五入し, 解答せよ。 途中で割り切れた場合は, 指定された桁まで 0 にマークすること。

(1) 1 月から 12 月までの辺量 x は次の通りであった。
-12, -9, -3, 3, 10, 17, 20, 19, 15, 7, 1, -8 (単位は ℃)
この 12 個の値の平均値は [ ア ].[ イ ]℃, 中央値は [ ウ ].[ エ ]℃ である。

(2) 1 月から 12 月までの 12 ヶ月を, 変量 x が 0℃ 未満の四つの月からなる A グループと, 0℃ 以上の八つの月からなる B グループとに分けて分析した。 このとき, A グループにおける変量 x の平均値は [ オカ ].[ キ]℃ であり, 分散は [ クケ ].[ コ ] である。

又, A グループにおける変量 y の平均値は 6.0℃ で, B グループにおける変量 y の平均値は 21.5℃ であった。 このとき, 1 月から 12 月までの変量 y の平均値は [ サシ ].[ ス ]℃ である。

変量 x と変量 y の相関図のデータの中で, 入力ミスが見つかった。 変量 x の値が 7℃, 変量 y の値が 30℃ となっている月の変量 y の値は, 正しくは 18℃ であった。

(3) この誤りを修正すると, 変量 y の平均値は [ セ ].[ ソ ]℃ 減少する。 又, 変量 y の分散は [ タ ] する。 但し, [ タ ] については, 当てはまるものを, 次の 0 〜 2 のうちから一つ選べ。

0 修正前より増加, 1 修正前より減少, 2 修正前と一致

(4) 修正前の変量 y の中央値は [ チ ]℃ であるが, 修正後には変量 y の中央値は [ ツ ]℃ となる。 [ チ ]. [ ツ ] の数値として適当なものを, 相関図を参考にして, 次の 0 〜3 のうちから一つずつ選べ。

0 13.5, 1 15.0, 2 16.5, 3 18.0

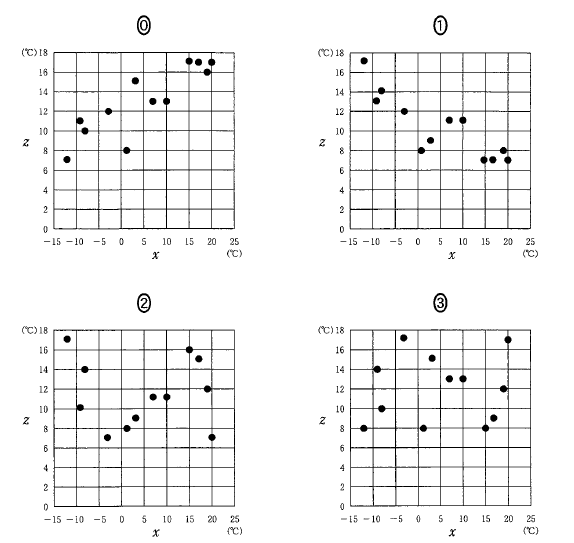
(5) 誤りを修正した後の寒暖の差 (最高気温と最低気温の差) を変量 z (= y -- x) とする。 変量 z の平均値は [ テト ].[ ナ ]℃ であり, 変量 x と変量 z の相関図として適当なものは [ ニ ] である。 但し, [ ニ ] については当てはまるものを, 次の次の 0 〜3 のうちから一つずつ選べ。

(6) この年の 1 月から 12 月までの最低気温 x と寒暖の差 z について, [ ヌ ] という傾向があると考えられる。 [ ヌ ] に当てはまるものを, 次の 0 〜 4 のうちから一つ選べ。

0 正の相関があり, 最低気温が高い月ほど寒暖の差が大きい。
1 正の相関があり, 最低気温が低い月ほど寒暖の差が大きい。
2 負の相関があり, 最低気温が高い月ほど寒暖の差が大きい。
3 負の相関があり, 最低気温が低い月ほど寒暖の差が大きい。
4 相関関係は殆どなく, 最低気温によって寒暖の差は影響を受けない。

第六問 (選択 20 点)

互除法 (ユークリッドの互除法) によって自然数 x, y の最大公約数を求める為, 次の 〔プログラム〕 を作成した。

〔プログラム〕

100 INPUT PROMPT "x=": X
110 INPUT PROMPT "y=": Y
120 IF X<Y THEN
[ ア ]
160 END IF
170 IF Y=0 THEN
180    PRINT [ イ ]
190    GOTO [ ウ ]
200 END IF
210 LET R=X
220 LET R=R-Y
230 IF R>=Y THEN GOTO 220
240 LET X=Y
250 LET Y=R
260 GOTO [ エ ]
270 END 

但し, [ ア ] は三行からなり, 変数 X と 変数 Y の値を交換する処理を表す。

(1) 〔プログラム〕 の [ ア ] に入る三行に当てはまるものを次の 0 〜 5 のうちから一つ選べ。

0 130 LET X=Y
　 140 LET Y=Z
　 150 LET Z=X

1 130 LET X=Y
　 140 LET Z=X
　 150 LET Y=Z

2 130 LET Y=Z
　 140 LET Z=X
　 150 LET X=Y

3 130 LET Y=Z
　 140 LET Z=X
　 150 LET X=Y

4 130 LET Z=X
　 140 LET X=Y
　 150 LET Y=Z

5 130 LET Z=X
　 140 LET Y=Z
　 150 LET X=Y

(2) [ イ ] に当てはまるものを, 次の 0 〜 5 のうちから一つ選べ。

0 X, 1 Y, 2 R, 3 X*Y, 4 X*R, 5 Y*R

(3) [ ウ ], [ エ ] に当てはまる行番号を, 次の 0 〜 5 のうちから一つずつ選べ。

0 100, 1 170, 2 210, 3 230, 4 260, 5 270.

(4) 〔プログラム〕 を実行して, 変数 X に 98, 又変数 Y に 54 を入力したとき, 170 行は [ オ ] 回, 220 行は [ カキ ] 回実行される。

(5) 〔プログラム〕 中の次の三行

210 LET R=X
220 LET R=R-Y
230 IF R>=Y THEN GOTO 220

で行う処理は, [ ク ] で置き換えることが出来る。 [ ク ] に当てはまるものを次の 0 〜 5 のうちから一つ選べ。 但し, INT(X) は X を超えない最大の整数を表す関数である。

0 LET R=X-INT(X/Y)*X
1 LET R=X-INT(Y/X)*X
2 LET R=X-INT(X/Y)*Y
3 LET R=Y-INT(Y/X)*Y
4 LET R=Y-INT(X/Y)*Y
5 LET R=Y-INT(Y/X)*X

〔プログラム〕 を変更して, x と y の最大公約数の代わりに x と y の最小公倍数を求めるようにしたい。
自然数 x と y の最小公倍数と最大公約数について, [ ケ ]。 このことを用いると, 新たに
LET T= [ コ ]
という行を 〔プログラム〕 の [ サ ] の部分に挿入し, 更に [ イ ] を [ シ ] に変更することで, x と y の最小公倍数を求めることが出来る。

(6) [ ケ ] に当てはまるものを, 次の 0 〜 4 のうちから一つ選べ。

0 最小公倍数が最大公約数よりも大きくなるのは, x > y の場合だけである
1 最小公倍数と最大公約数の和は, x と y の和に等しい
2 最小公倍数と最大公約数の差は, x と y の差に等しい
3 最小公倍数と最大公約数の積は, x と y の積に等しい
4 最小公倍数を最大公約数で割った商は, x を y で割った商に等しい

(7) [ コ ] に当てはまるものを, 次の 0 〜 5 のうちから一つ選べ。

0 X>Y, 1 X<Y, 2 X+Y, 3 X-Y, 4 X*Y, 5 X/Y

(8) [ サ ] に当てはまるものを, 次の 0 〜 5 のうちから一つ選べ。

0 100 行の前, 　　　　　1 100 行と 110 行の間
2 160 行と170 行の間, 3 200 行と 210 行の間
4 250 行と 260 行の間, 5 260 行と 270 行の間

(9) [ シ ] に当てはまるものを, 次の 0 〜 5 のうちから一つ選べ。

0 T/X, 1 T/Y, 2 X/T, 3 T, 4 X*T, 5 Y*T

解答へ。

センター試験の目次に戻る。