面積とは二次元の量, つまり平面上の図形に対して定められるものであった。 体積はそれに対し三次元の量, つまり立体図形に対して定められるものである。
何でもそうだが, 次元が一つ上がったものに関しては殆ど, 次元を一つ上げて考えるのが常套手段である。
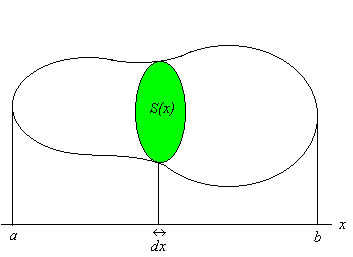
或立体図形が空間上にあり, x 軸について直交する方向の断面が x に関する函数 S(x) として与えられているとしよう。
面積が, 縦方向の長さ f(x) に, 微小な長さ dx を掛けた非常に薄い長方形の和 ∫ab f(x)dx であったように, S(x) に直角方向の微小な長さ dx を掛けると (なんとも名状しがたいが) 柱状体の体積になる。
従って, こいつを a から b 迄足し合わせると体積 V = ∫ab S(x)dx になる。 略記号 V は volume の略。

ところで S(x) はどうやって出すかというと, x 軸に直交方向に y 軸を作り, y 軸に直行する方向の S(x) を作っている図形の切断線の長さを f(y) とすれば S(x) =∫a(x)b(x) f(y)dy になる。 先程の式に代入すると V = ∫ab S(x)dx = ∫ab ∫a(x)b(x) f(y)dydx となる。 これを累次積分 repeated integral, iterated integral という。 体積は本当は二重積分 double integral で定義されるのだが, 実際問題としては累次積分に帰結できないと計算できない事が多い。 この話はもっとずっと後でちゃんとしよう。 (重積分 multiple integral という)
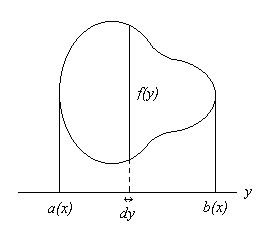
例として錐体の体積を計算してみよう。
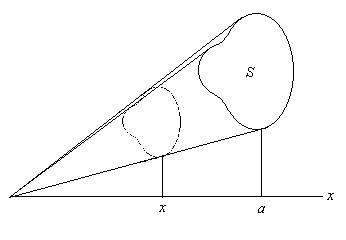
底面積が S で, 高さが a の錐体が図のように与えられていたとする。 x のところにある断面の面積は相似比が a : x だから, 面積比が a2 : x2. 従って a2 : x2 = S : (面積) だから, 面積が Sx2/a2 と求まる。よって
V = ∫0a (Sx2/a2)dx = (S/a2)∫0a x2 dx = (S/a2)[x3/3]0a =(S/a2)(a3/3) = aS/3.
即ち (傾いていようが, 底面の形がどのようであろうが) 錐体の体積は (底面積)×(高さ)÷3 である。
ユークリッドの原論では三角錐について非常に上手い方法を用いて, その体積が三角柱の 1/3 なることを求めているので紹介しておこう。
原論 第 12 巻
命題 7
任意の (斜) 三角柱 prism は三つの (体積の) 等しい (斜)
三角錐 pyramids に分割される。
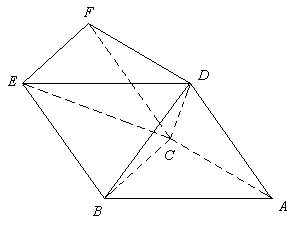
証明
三角柱の下底面を △ABC, 上底面を (順に対応して) △DEF としよう。
BD, EC, CD を結ぶ。
四角形 ABED は平行四辺形で, BD はその対角線だから,
△ABD ≡ △EBD [第 1 巻 命題 34].
故に C を頂点とし △ABD を底面とする三角錐と,
同じ C を頂点とし △EBD を底面とする三角錐は共に体積が等しい。[第 12 巻命題 5]
しかし, C を頂点とし △EBD を底面とする三角錐は D を頂点とし
△EBC を底面とする三角錐とも見ることが出来る。
故に C を頂点とし △ABD を底面とする三角錐 は D を頂点とし △EBC を底面とする三
角錐と体積が等しい。
今度は平行四辺形 FCBE とその対角線 CE に着目すると
△CEF ≡ △CBE.
故に D を頂点とし △BCE を底面とする三角錐と, 同じ D を頂点とし △ECF
を底面とする三角錐は共に体積が等しい。
そして, 三角錐 D-BCE は三角錐 C-ABD と体積が等しいことが先に示されている。
即ち三角錐 D-CEF と三角錐 C-ABD も体積が等しい。
以上によって三角柱 ABCDEF は 三角錐 C-ABD, D-EBC, D-EFC
の三つの体積の等しい三角錐に分割された。
ところで三角錐 C-ABD は三角錐 D-ABC でもある。
従って [Porism.]
三角錐は同じ底面をもち同じ高さをもつ三角柱の 1/3 の体積である。
途中で使っている命題 5 であるが:
命題 5
同じ高さの三角錐同士の体積比は, 底面積比に等しい。
ここの議論は果てしなく面倒である。所謂 Francesco Bonaventura Cavalieri (カヴァリエリ 1598--1647) の原理を使うのとは違う証明がしてある。
カヴァリエリの原理とは一次元下げて平面図形でいえば, ある, 平行線で切っていったときに, いつもその線分の長さが一定の比 a : b になっていれば, 全体の面積比もやはり, a : b になるというもので, 積分が分かっていれば, 当然の原理である。
体積に関するカヴァリエリの原理とは, ある平行な平面で切っていったときに, いつも切断面が一定の比 a : b になっていれば, 全体の体積比もやはり a : b になるというものである。
当然の原理ではあるが, 中国にはこのカヴァリエリの原理を用いて, 球の体積を求めた人がいる。 詳細はこちら。
The Thirteen Books of Euclid's Elements, Sir Thomas L. Heath, et al. vol. III, Dover.