, C
は積分定数。合成函数の微分法を思い出していただこう。 極めていいかげんではあったが
(f(g(x))' = g'(x)f'(g(x))
ということを説明した。 これを積分の言葉に翻訳すると, それが置換積分 integration by substitution となる。
先ず都合により, 変数を x の変わりに t と置くと (f(g(t))' = g'(t)f'(g(t)), 又この式で x = g(t) と置くと (f(x))' = g'(t)f'(g(t))両辺に integral をつけて
∫(f(x))'dx = ∫g'(t)f'(g(t))dt
ここで f' を改めて f と置き直すと
∫f(x)dx = ∫f(g(t))g'(t)dt.
さてここで次の定義を置こう:
微分可能な函数 f(x) に対し,
df(x) = f'(x)dx
を微分形式 differential form と呼ぶ。 この式の両辺を dx で割ると, Lagrange の記号と Leibniz の記号の橋渡しをしているだけの式
df(x)/dx = f'(x)
になりますから, たいした式ではありません --- 勿論微分形式には深い意味があるのですが (笑)。
ここで x = g(t) としますと, 両辺に (外) 微分記号 d をつけると
dx = dg(t) = g'(t)dt
となります。 従って x = g(t) と, dx = g'(t)dt とを代入することによって
∫f(x)dx = ∫f(g(t))g'(t)dt
となるので, 置換積分は只単に代入しているだけの式となるわけです。
例:
(1) a ≠ 0, F'(x) = f(x) とする時
∫f(ax + b)dx = F(ax + b)/a + C, C は積分定数。
t = ax + b と置くと, dt = d(ax + b) = adx. 故に dx = dt/a. 代入して
左辺 = ∫f(t)dt/a = F(t)/a + C = F(ax + b) + C, C は積分定数。
(2) , C
は積分定数。
t = f(x) と置くと, dt = df(x) = f'(x)dx. 従って
左辺 = ∫f'(x)dx/f(x) = ∫dt/t = log |t| + C = log |f(x)| + C, C は積分定数。
注: 以後これらの二つの積分は黙って公式として使う。
(3) 
, これは t = 1 + x
と置いても, 
と置いても出来る。
先ず最初の方法でやると
与式 = ∫(t - 1)t-1/2 dt = ∫(t1/2 - t-1/2)
dt
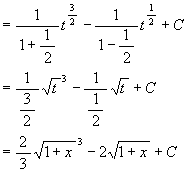
C は積分定数。
後のほうでやると t2 = 1 + x より dx = 2tdt だから
となって同じ結果を得る (当然だ)。
上記(1), (2) の二つの公式を用いた例:
(1) ∫cos2x dx = ∫((1 + cos 2x)/2)dx … 半角の公式
= (1/2)∫(1 + cos 2x)dx = (1/2)(x + (1/2)sin 2x) + C
= x/2 + (sin 2x)/4 + C, C は積分定数。
(2) ∫sin mx cos nx dx (以下しばらく mn ≠ 0)
a) m = ±n の場合: sin 2x = 2sin x cos x を用いて
与式 = ∫sin (±n)x cos nx dx = ±∫sin nx cos nx dx = ±(1/2)∫sin 2nx
dx
= ±(1/2)(1/(2n))(- cos 2nx) + C
従って 与式 = ±(1/(4n))cos 2nx + C, C は積分定数。 (複号は逆順)
b) m ≠ ±n の場合: 積を和に変える公式を用いて
与式 = (1/2)(∫sin(m+n)x dx + ∫sin(m-n)x dx)
= (1/2)(-(1/(m+n))cos(m+n)x - (1/(m-n))cos(m-n)x) + C
=-(1/2)((1/(m+n))cos(m+n)x + (1/(m-n))cos(m-n)x) + C,
C は積分定数。
(3) ∫sin mx sin nx dx
a) m = ±n の場合: 半角の公式を用いて
与式 = ±∫sin2 nx dx = ±(1/2)∫(1 - cos 2nx)dx
= ±(1/2)(x - (1/(2n))sin 2nx) + C, C は積分定数。
b) m ≠ ±n の場合: 積を和に変える公式を用いて
与式 = (1/2)∫(cos(m-n)x - cos(m+n)x)dx
= (1/2)((1/(m-n))sin(m-n)x - (1/(m+n))sin(m+n)x) + C,
C は積分定数。
(4) ∫cos mx cos nx dx
a) m = ±n の場合: 半角の公式を用いて (1) と同様にして
与式 = (1/2)(x + (1/(2n))sin 2nx) + C, C は積分定数。
b) m ≠ ±n の場合: 積を和に変える公式を用いて
与式 = (1/2)∫(cos(m+n)x + cos(m-n)x) dx
= (1/2)((1/(m+n))sin(m+n)x + (1/(m-n))sin(m-n)x) + C,
C は積分定数。
(5) a≠0, 1 の定数とき ∫axdx = ∫exlog a dx = exlog a/log a + C = ax/log a + C, C は積分定数。
(6) a≠0 の定数のとき 
… (a) だから
∫dx/(x2-a2) = (1/(2a))∫(1/(x-a) - 1/(x+a))dx
=(1/(2a))(log |x - a| - log |x + a|) + C =
,
C は積分定数。
さてここで無造作に最初の式 (a) を出してしまったが, 実はこれは結構面倒なのである。 先ず分母を因数分解して (x2-a2) = (x-a)(x+a) に関しては異論がないであろう。そこで
という式が成り立つと仮定して, 定数 A, B を求める。 右辺だけ一つの分数に纏めると
さて, この結果が元の式の左辺 1/(x2-a2) と一致しなければならない。 ということは分母が一致しているから 1 = (A + B)x - a(A - B) でなければならない。 ここの等号は x の式としての等号なのだから当然
A + B = 0 (左辺は x に関し 0 次式だから)
a(A - B) = 1
でなければならない。 この式を解くと A = 1/(2a), B = -1/(2a) となるのである。 このやり方を部分分数への分解という。
(7) ∫tan x dx = ∫(sin x/cos x) dx = -∫(-sin x/cos x)dx = -∫d(cos x)/cos
x
= -log |cos x| + C, C は積分定数。
ここでは t = cos x と置くと, dt = -sin x dx となることを用いているのだが, いちいち変数変換をしていると面倒なので, 私はこのように書いてしまうことが多い。
(8) ∫cot x dx = ∫(cos x/sin x) dx = ∫d(sin x)/sin x = log |sin x| + C,
C は積分定数。
(9) ∫sin x sec2x dx = -∫d(cos x)/cos2x = -∫(cos
x)-2 d(cos x)
= (cos x)-1 + C = sec x + C, C は積分定数。
ここで cos-2 x とかくと, 逆三角函数 cos-1 x があるので紛らわしいからやめたほうがいい。
(10) ∫cot x csc x dx = ∫(cos x/ sin2 x) dx = ∫(sin x)-2
d(sin x)
= -(sin x)-1 + C = -csc x + C, C は積分定数。
(11) ∫dx/(x log x) = ∫(dx/x)/log x = ∫d(log x)/log x = log |log x| + C,
C は積分定数。
(12) ∫dx/(1 + x2). これは x = tan t と置く。すると
1 + x2 = 1 + tan2 t = 1/cos2 t
で, dx = d(tan t) = d(sin t/cos t) = dt/cos2t であるから
与式 = ∫dt = t + C = tan-1 x + C, C は積分定数。
(13) 
. これは x = sin t
と置くと, 
であるが,
最後のところで符号の問題が生じるので, sin-1 x
の主枝である -π/2 ≦ t ≦ π/2 であるとする。 こうすると dx
= cos t dt であるから
与式 = ∫dt = t + C = sin-1 x + C, C 積分定数
他にもあるが, この辺にしておこう。