極限

1. 収束と極限値
2. ε - δ 論法
3. 収束の簡単な例
4. 定発散
5. 振動
6. 極限の纏め
7. 極限に関する定理
8. 極限の計算

収束と極限値

普通の高校の教科書には, 数列の極限についてこんなことが書いてある。

無限数列 {a_n} に於いて, n が限りなく大きくなると, a_n の値が一定の値 α に限りなく近付くとき, 数列 {a_n} は α に収束する converge (或いは 収斂 (しゅうれん) する) といい, 又は数列 {a_n} の極限値 limit value は α であるといい,

或いは,

n→∞ の時, a_n→α,
a_n→α (as n→∞),
,
,

と書く。 この site ではあまり画像を使いたくないため,

lim_n→∞ a_n = α

のように書いてあることが多い。

さて, いつも問題になるのは, 斜体で書いた 「限りなく大きくなる」, 「限りなく近付く」 というのはどういう意味なのか ? ということである。 計算上は:

数列 {a_n} の一般項 a_n を表す式に, 直接 --- 或いはある程度の technique を要することもあるが --- n = ∞ を代入したときに, その 「標準部分」 が (±∞ を含まない標準) 実数 α (即ち超実数としては α±0) になるとき

が, 「限りなく大きくなる」, 「限りなく近付く」 という意味になる。 しかし勿論これでは 「近付く」 という意味ははっきりしない。

ε - δ 論法

暫く難しい話を書く。 (飛ばしたければここ)

Archimedes (アルキメデス) は a > 0 とすると ∀n∈N(0 ≦ ε < a/n ⇒ ε = 0) ということを主張した。 これは Archimedes の公準と呼ばれている。 もしもこうでないとすると ∀n∈N(n ≦ a/ε) となって, 自然数が有限になってしまう。

現在の標準解析学では, これをお手本にして極限を次のように定義している。

∀ε > 0∃N∈N(n > N ⇒ |a_n - α| < ε).

意味は, 「任意の正の数 ε に対し, ある自然数 N が決められて, N よりも大きい全ての番号 n について |a_n - α| < ε, つまり, a_n と極限値 α との間が, 最初に決められた誤差 ε よりも小さくできる」 ということである。 これが悪名高き ε - δ 論法 (或いはこの場合は ε- N 論法ともいうらしいが) である。 私はこれが分かるのに三年くらいを要したので, 皆さんがすぐ分からなくてもがっかりしなくて良い (笑)。

つまり n が ∞ に 「近付いていく」 時に, |a_n - α| < ε 即ち -ε < a_n - α < ε, 即ち α - ε < a_n < α + ε, 即ち, a_n が α のすぐそば (ε 近傍) に凝集しているということである。

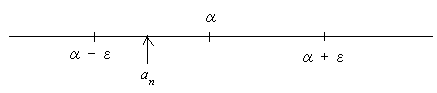
もう少し解説すると, こういうことである:

非常に疑い深い人がいたとして, a_n が α に限りなく近付くという主張に疑いを持ったとしよう。 もしも近付かないとすれば, a_n と α の差が, ある一定数よりは小さくならないこと (つまり ∃ε >0∃N∈N(n > N ⇒ |a_n - α| ≧ ε) ということ) を示さなければならない。 つまり, 彼はこういうことを言ってくるはずだ。 「そんなことはないだろう, どんなに頑張ったって, 誤差 1/10000 以下には出来ないに違いない」。 これに対して, あなたは一寸計算して (例えば) 「ほら, 100 万番以降では 1/10000 以下になっていますよ」 ということを言ってやればいい。 更に彼が 「1/10000 以下には出来たかもしれないが, 1/10⁸ 以下には出来ないに違いない」 と言ってきたら, もうちょっと計算して (例えば) 「ほら 1 億番以降では 1/10⁸ 以下になっていますよ」 といってやればいい, 更に... というわけ。

さて, この 「ε - δ 論法」 による定義が, さっきの Archimedes の公準とどういう関係にあるかというと, 特に ν を自然数として ε = 1/ν とすると, 定義は

∀ν, ∃N∈N(n > N ⇒ |a_n - α| < 1/ν)

だが, 極限にいくと Archimedes の公準から

|lim_n→∞a_n - α| < 1/ν ⇒ |lim_n→∞a_n - α| = 0

となるからである。

簡単な例

(1) lim_n→∞ (1/n) = 1/∞ = +0 ≡ 0 (mod ±0).

これを lim_n→∞ (1/n) = 0 と書く (超実数を導入した部分の, 途中経過を書かない)。 又は 1/n → 0 as n → ∞ 等。

1 > 1/2 > 1/3 > 1/4 > 1/5 > …… > 1/n > …… > 0

というのが 「0 に近付く」 という雰囲気である。

(2) lim_n→∞ (1 - 1/(2n)) = 1 - 1/(2×∞) = 1 - 1/∞ = 1 - 0 ≡ 0 (mod ±0).

答案では lim_n→∞ (1 - 1/(2n)) = 1 - 0 = 0. 又は 1 - 1/(2n) → 1 - 0 = 0 as n → ∞ 等。

(3) (-1)ⁿ/n.

(-1)ⁿ はとにかく +1 か -1 に決まっている。 どっちにしても ±1/∞ = ±0 ≡ 0 (mod ±0) だから, lim_n→∞ ((-1)ⁿ/n) = 0.

(4) c を (普通の) 実数とすると

lim_n→∞ c = c (代入するところがないから).

定発散

n が限りなく大きくなるとき, a_n の値が限りなく大きくなるとき, a_n は正の無限大に発散する diverge といい, a_n < 0 で |a_n| の値が限りなく大きくなるとき, a_n は負の無限大に発散するという。 このとき ±∞ は {a_n} の極限と呼ばれる (極限値ではない)。 ここで 「限りなく大きくなる」 といい, 「±∞ に近付く」 と言わなかったのは伝統に従ったまでで, その方が分かり易ければそれでも良い。 因みに L. Schwartz は Théorie des Distributions 3/e, Chapter 3, §1 で 「+∞ に収束する」 という表現をしているので, 定発散の時, 「発散する」 というのも単に伝統に従ったまでとも言える。

超準解析的には, a_n の式に n = ∞ を代入したときに +∞, -∞ の値になることが定発散である。

ε - δ 論法で述べると次の通り。 a_n が正の無限大に定発散するとは ∀R >0∃N∈N(n > N ⇒ a_n > R). つまり任意の正の数 R に関し, ある番号以上, a_n > R と出来る。

記号では lim_n→∞a_n = +∞, lim_n→∞a_n = -∞ などと書く。

簡単な例)

lim_n→∞ n = ∞, lim_n→∞ n² = ∞,
lim_n→∞ (-n) = -∞, lim_n→∞ (-2n) = -∞.

振動

収束もしないし定発散 (即ち正又は負の無限大に発散) しもしない数列は振動する oscillate 又は (不定) 発散するという。 この場合極限は存在しない。

簡単な例)

(1) {(-1)ⁿ}, これは -1, 1, -1, 1, -1, ... のようになっていて, 「最後」 が +1 か -1 か分からない。 このような場合, , 等と書いたりする。 lim inf を下極限 inferior limit, lim sup を上極限 superior limit という。

(2) {(-2)ⁿ}, これは -2, 4, -8, 16, -32, ...... の様になっていて, 絶対値は段々大きくなっていくが, +, - は交互に現れるので, 定まらない。 この場合 lim inf_n→∞ (-2)ⁿ = -∞, lim sup_n→∞ (-2)ⁿ = +∞ である。

(3) {sin n} これはもう全然無茶苦茶で傾向がない。 しかし -1 ≦ sin n ≦ 1 であり, π が無理数であることから im inf_n→∞ sin n = -1, lim sup_n→∞ sin n = 1 である。

極限の纏め

数列の極限

収束する …………………………………………… 極限値が存在する

発散する

定発散する (正の無限大, 負の無限大) …… 極限が存在する

振動する (不定発散する)

定理

これから使う定理を二つ掲げるが, 最初は証明は読まなくても良い。 証明は ε - δ 論法を用いて行われる。

定理

lim_n→∞ a_n = α ⇒ (∃M (|a_n| < M ) & |α| ≦ M).

| α| ≦ M に等号が入っているのは誤りではない。 例えば, a_n = 1 - 1/n < 1 であるが, lim_n→∞ a_n = lim_n→∞ (1 - 1/n) ≦ 1 であるから。 勿論 |a_n| < M の方に等号を入れても良い。

特に

lim_n→∞ a_n = α, lim_n→∞ b_n = β, a_n < b_n ⇒ α ≦ β.

勿論 a_n ≦ b_n としても良い。

定理

数列 {a_n}, {b_n} の両方ともが収束するとき, c を定数として

(1) lim_n→∞ ca_n = c・lim_n→∞ a_n.
(2) lim_n→∞ (a_n ± b_n) = lim_n→∞ a_n ± lim_n→∞ b_n, resp.
(3) lim_n→∞ (a_n・b_n) = (lim_n→∞ a_n)・(lim_n→∞ b_n).
(4) 更に ∀n(b_n ≠ 0) & lim_n→∞ b_n ≠ 0 の時
　　

最後の (4) では実は極限を考えているのだから, ∀n(b_n ≠ 0) という仮定は過大で, ∃N∈N(n > N ⇒ b_n ≠ 0) で充分なのだった。

証明はここ。

極限の計算

1. (分母の) 最高次で割る。
2. 無理式 (特に差形) は有理化。
3. 係数比較 (n → ∞ の時)
4. rⁿ の形は r による場合分け (r = ±1 が分かれ目)。
5. 不等式を作り, 挟み撃ち。
6. de l'Hospital (ド・ロピタル) の定理。 (或いは Taylor 展開)。
7. 分数式の極限値が存在する場合
   　　分母 → 0 ⇒ 分子 → 0,
   　　分子 → 0 ⇒ 分母 → 0.

例はこちら。

次へ
数列の極限の目次へ