定義と例

[定義]

数列 a₁, a₂, a₃, ..., a_n, ... の各項を + の記号で結んで出来る式

a₁ + a₂ + a₃ + … + a_n + … (1)

を無限級数 infinite series といい, 記号 Σ_n=1^∞ a_n で表す。

無限級数 (1) の初項から第 n 項までの和

S_n = a₁ + a₂ + a₃ + … + a_n = Σ_k=1ⁿ a_k

を, (1) の無限級数の第 n 部分和 partial sum といい, 数列 {S_n} が収束して, その極限が S であるとき, 即ち lim_n→∞ S_n = S の時, (1) は収束する converge といい, S を (1) の和 sum という。 又収束しないときは (1) は発散する diverge といい, 和は考えない。

無限級数の計算が最も簡単にでき, しかも簡単なのが次の page で扱う無限等比級数である。 従って無限等比級数である場合とそうでない場合とは別に考えた方が良い。

一般には部分和を考えて, その極限を取る。 というのは無限級数とは定義に見えるように, 部分和の極限に他ならないからである。 勿論幾つか良く知られた級数の収束判定法というのがあるが, ここでは余り深く立ち入らない。

例:

[1] 次の無限級数の収束・発散を調べ, 収束するものは, その和を求めよ。

(1) 1 + 2 + 3 + … + n + ….

(2) 1² + 3² + 5² + … + (2n - 1)² + ….
(3) .

(4) .

(5)

解) 以下で第 n 部分和を S_n と置く。

(1) S_n = n(n + 1)/2 = n²(1 + 1/n)/2 → +∞ (as n → ∞).

∴ lim_n→∞ S_n = +∞. よって発散する。

(2) S_n = Σ_k=1ⁿ (2k - 1)² = Σ_k=1ⁿ (4k² - 4k + 1)
= 4×n(n + 1)(2n + 1)/6 - 4×n(n + 1)/2 + n
= (2/3)n(n + 1)(2n + 1) - 2n(n + 1) + n
= (2/3)n(2n² + 3n + 1) - 2n(n + 1) + n
= (1/3)n(4n² + 6n + 2 - 6n - 6 + 3)
= n(4n² - 1)/3 = n³(4 - 1/n²)/3 → +∞ (as n → ∞).

従って発散する。

(3)

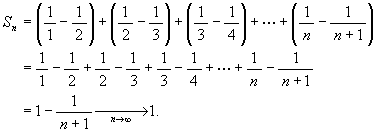
従って収束して, 和は 1.

[注意] 有限和 (部分和) だったから一行目から二行目のように括弧をはずして順番を勝手に変えたり出来るのであって, 無限和でこれをやってはいけない。 有名な例は

1 - 1 + 1 - 1 + 1 - 1 + …  は発散,
(1 - 1) + (1 - 1) + (1 - 1) + … = 0,
1 + (- 1 + 1) + (- 1 + 1) + (- 1 + 1) + … = 1.

(4) であるから
 

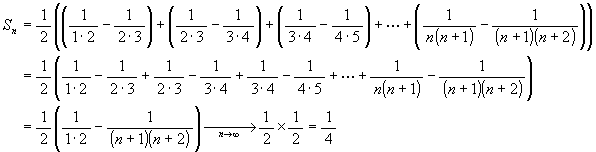
だから収束して和は 1/4.

(5) 各項を a_n と置くと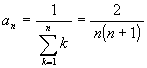 であるから, (3) と同様にして, 収束して和は 2.

[2] 次の各問に答えよ。

(1) 初項から第 n 項までの和が n(n + 7)/2 で与えられる数列 {a_n} に関して, 次の無限級数の収束・発散を調べ, 収束するときはその和を求めよ。

(2) 初項から第 n 項までの和が n(n + 4) で与えられている数列 {a_n} に関して, 次の無限級数の収束・発散を調べ, 収束するときはその和を求めよ。

解) 以下では数列 {a_n} の初項から第 n 項までの和を T_n とし, 与えられた無限級数の第 n 部分和を S_n と置く。

(1) T_n = (n² + 7n)/2. 従って

a₁ = T₁ = 8/2 = 4,
n ≧ 2 ⇒ a_n = T_n - T_n-1 = (n² + 7n)/2 - ((n -1)² + 7(n - 1))/2
= (n² + 7n)/2 - (n² - 2n + 1 + 7n - 7)/2
= (n² + 7n - n² - 5n + 6)/2
= (2n + 6)/2 = n + 3. (これは n = 1 も含んでいる)。

∴a_n = n + 3.

従って

S_n = 1/(4・5) + 1/(5・6) + 1/(6・7) + … + 1/((n + 3)(n + 4))
= (1/4 - 1/5) + (1/5 - 1/6) + (1/6 - 1/7) + … + (1/(n + 3) - 1/(n + 4))
= 1/4 - 1/(n + 4) → 1/4 as n → ∞.

従って収束してその和は 1/4.

(2) T_n = n² + 4n. 従って

a₁ = T₁ = 5,
n ≧ 2 ⇒ a_n = T_n - T_n-1 = (n² + 4n) - ((n - 1)² + 4(n - 1))
= n² + 4n - (n² - 2n + 1 + 4n - 4)
= n² + 4n - n² - 2n + 3 = 2n + 3. (これは n = 1 も含んでいる)

∴a_n = 2n + 3.

ここで

1/(a_na_n+2) = 1/((2n + 3)(2n + 7)) = (1/4)(1/(2n + 3) - 1/(2n + 7))

であるから (項の打ち消し合い方に注意)

S_n = 1/(5・9) + 1/(7・11) + … + 1/((2n + 3)(2n + 7))
= (1/4)((1/5 - 1/9) + (1/7 - 1/11) + (1/9 - 1/13) + (1/11 - 1/15) + … + (1/(2n - 1) - 1/(2n + 1)) + (1/(2n + 3) - 1/(2n + 7)))
= (1/4)(1/5 + 1/7 - 1/(2n + 1) - 1/(2n + 7))
→ (1/4)×(1/5 + 1/7) = (1/4)×(12/35) = 3/35 (as n → ∞).

従って収束してその和は 3/35.

次へ
無限級数の目次へ