[定義]
長さが 1 の vector を単位ベクトル unit vector という。
そのわけは, 長さが単位長 unit length だからである。
a ≠ 0 とするとき
e+ = a/|a| は a と同じ向きの単位ベクトル,
e- = -a/|a| は a と逆向きの単位ベクトル。
従って, a ≠ 0 と平行は単位ベクトルは ±a/|a|.
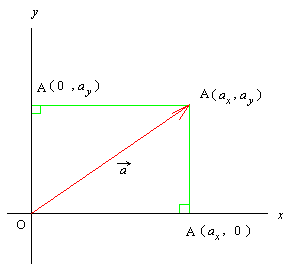
さて, お馴染みの xy 平面を考える。 いつものように原点 O を置く。
座標軸上に単位点 Ex(1, 0), Ey(0, 1) を採り, ex = OEx, ey = OEy と置く。 明らかに |ex| = |ey| = 1 であり, これらは一次独立である。 この時 ex, ey を平面の基本ベクトル fundamental vectors といい, {ex, ey} を平面の標準基底 canonical base, canonical basis という。
今, 平面上に A(ax, ay) という点を採り, a = OA と置く。 この時 a ∈ RexÅ Rey だから ∃x∃y(a = xex + yey) であるが, 図から分かるように a = axex + ayey である。

しかも, 別にもしも a = xex + yey と書けていたとすると, 辺々引いて 0 = (x - ax)ex + (y - ay)ey となるが, ex, ey は一次独立だから x = ax, y = ay. 即ち, a = axex + ayey という表示は一意的である。
この場合の ax, ay を各々vector a の x 成分 (x component), y 成分 (y component) といい, 合わせて vector a の成分 components という。 又今後簡単の為に a = (ax, ay) と書き, vector a の (標準基底による) 成分表示 representation by components という。
簡単に言えば, vector a の成分とは a の始点を原点に持ってきたときの終点の座標のことである。
さて, a = (ax, ay), b = (bx, by) とするとき
は明らかであろう (言葉で言えば対応する成分同士が等しいときに限って vectors として等しい)。 何故なら成分表示の定義 (及び一次独立の定義) から
a = b ⇔ axex + ayey = bxex + byey ⇔ (ax - bx)ex + (ay - by)ey = 0 ⇔ ax = bx∧ ay = by
だからである。
以下大体成分表示の定義に戻って, 次のような公式を得る:
a + b = (ax + bx,
ay + by),
a - b = (ax - bx, ay
- by),
ka = (kax, kay).
標語的に言うと, 成分表示の和と差は成分毎の和と差, scalar 倍は成分毎に分配, ということである。
さて, ここで 「平行と一次独立」 の最後に書いた二つの定理をもう少し厳密に証明しておく。
先ず 「平面上の vectors について a1 と a2 が一次独立 ⇔ ¬(a1 || a2)」 はこれを証明する代わりに, その対偶を取ると 「平面上の vectors について a1 || a2 ⇔ a1 と a2 が一次従属」 であって, これは明らかである。
∃a,b(V2 = RaÅ Rb) については, a = (ax, ay), b = (bx, by) が ¬(a || b) とするとき ∀c = (x, y) に対し c = ka + mb となる k, m が求まればよい。 これを成分で書くと
x = kax + mbx, … (1)
y = kay + mby … (2)
である。 k を求めよう: by(1) - bx(2): byx - bxy = (axby - aybx)k. 従って axby - aybx ≠ 0 であるならば k の値は求まる。 m の方も同様である。 さてもしも axby - aybx = 0 とすると, axby = aybx であるから, 今仮に bxby ≠ 0 として両辺をこれで割り ax/bx = ay/by = t と置くと, ax = tbx, ay = tby となる。 bx = 0 の時は, axby = 0 であるから ¬(a || b) より by ≠ 0, 従って ax = 0 だから, 「ax = tbx, ay = tby」 は成立している。 by = 0 の時も同様である。 従って一般に ax = tbx, ay = tby. それはつまり a ∈ Rb であるから, 一次独立の仮定に反する。 従って, 上記 (1), (2) の連立方程式は解ける。 従って証明された。
尚, 集合論では (x, y) = {{x}, {x, y}} と書き順序対 ordered pair という。 これに関しては (x, y) = (x', y') ⇔ x = x' ∧ y = y' ということが分かればよい。 この順序対を使って直積集合 direct product
A×B = {(x, y)| x ∈ A ∧ y ∈ B}
というものが定義される。
Vectors の成分を直積集合の言葉で書くと V2 = R×R というように書き習わしているが, この R 2 に和, 差, 実数倍というものを上記の成分表示の公式のように定義したものが平面の vectors だということが出来る。
記号 V2 はこの R 2 を反映している。
専門家向けには, 写像 R 2 → V2: (x, y)→xex + yey が普遍性 universality を持つ, というように表現される。 詳しくは代数学の専門書を見ると良い (最初に索引を見て普遍性という言葉が出ていないような本には多分出ていない)。