△ABC の三頂点を通らない直線 l と三直線 B∪C, C∪A, A∪B との交点を各々 P, Q, R とするならば
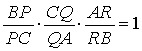
(線分の長さに符号をつけて考える場合は = -1 である)
Ceva の定理の証明中, α と β の値を求めたところで事実上次の式が証明されている。
(BP/BC)(CQ/QA)(AD/DP) = ((1 - t)/1)(s/(1 - s))(α/(1 - α))
= (1 - t)(s/(1 - s))((1 - s)/(s(1 - t))) = 1.
これが Menelaus (メネラウス) の定理と呼ばれるものである。 通常使われる形でこれを述べておこう。
定理 [Menelaus]
△ABC の三頂点を通らない直線 l と三直線 B∪C, C∪A, A∪B との交点を各々 P, Q, R とするならば
(線分の長さに符号をつけて考える場合は = -1 である)
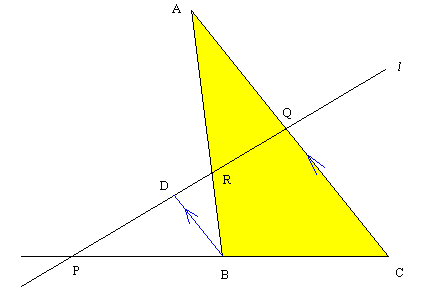
Vector に拠る証明は既に与えてあるので, 初等的な証明を書いておく:
図のように BD || CQ となる点 D を l 上に採る。
△PBD ∽ △PCQ より BD = CQ・PB/PC.
次に △RBD ∽ △RAQ より BD = QA・RB/AR.
これらから CQ・PB/PC = QA・RB/AR.
従って (PB/PC)(CQ/QA)(AR/RB) = 1□
私はこの定理を良く覚えていないので, この初等的な証明の方法を繰り返し用いている。