次に加法を手がかりにして実数倍というのを考えていく。 (通常の text books よりは細かいと思う)
最初に a + a という vector を考えよう。 中学で文字式を学んだ人は, これを 2a と書きたい衝動に駆られるのではないだろうか。 そこで
2a = a + a
となるように 2 倍, 更に一般に n 倍というのを決めてしまおうというわけである。 先ず次のように定める (帰納的定義):
1a = a.
n が正の整数, 即ち n = 1, 2, 3, 4, ... の時
(n + 1)a = na + a.
2 倍というのはすぐ上の式で特に n = 1 としたものであり
3a = (2 + 1)a = 2a + a
= a + a + a,
4a = (3 + 1)a = 3a + a =
a + a + a + a,
等々。 つまり na とは a を n 個足したものだということになっている。
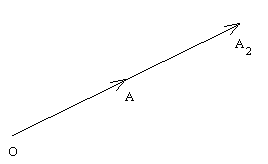
では (矢印として) 2a はどういう vector になっているだろうか。 それを調べるために a = OA と置こう。 この時上記に従って 2a = a + a とするのだが, 平行四辺形則で足算をすることは不可能に近いので, 繋ぎ合わせの法則に拠ることにしよう。
先ず, (二倍に関する点ということで) a = AA2 となる点 A2 を描く。 この時
2a = a + a = OA + AA2 = OA2
となる。 つまり 2a は vector a と向きが同じで長さが二倍の vector ということである。

同様に a = A2A3 となるような A3 を置けば, 3a = 2a + a = OA2 + A2A3 = OA3 であるから, 3a は a と向きが同じで, 長さが 3 の vector ということになる。
以下同様であるから, 一般に n を正の整数とするとき, na は vector a と向きが同じで, 長さが n 倍の vector を表していることになる。 特に
|na| = n|a|.
さて, このように決めると vectors a, b と正の整数 n, m に対して次のことが成立していることが分かる (図を描いてみればよい)。
n(a + b) = na + nb,
[scalar 分配法則]
m(na) = (mn)a, [scalar 乗法の結合法則]
(m + n)a = ma + na. [vector 分配法則]
例えば vector 分配法則で, n = 3 の時は, 次のようになる。
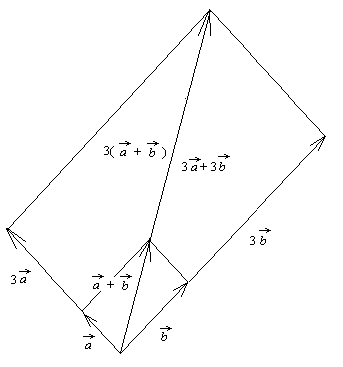
Scalar 乗法の結合法則は又, 「a の長さを n 倍したもの」 の m 倍が, 「a の長さを (nm) 倍したもの」 と同じであることからも分かる。
さて, 本当はここで -1 倍とか 0 倍とかの方を考えた方が論理的なのだが, 定義の気分があまりよく伝わらないといけないので, 先に正の有理数倍を考えてみることにする。 論理的なものを望む人, 気になる人は先に負の数倍の方を読むと良い。
正の有理数倍を考えるために, 正の有理数 r に対し, r を規約分数 (もうこれ以上約分できない分数) として, 正の整数 m, n を用いて n/m と表すことにしよう。 これから ra = (n/m)a について考えていく ((n/m)a = (na)/m と書いても同じ)。
今 x = ra = (n/m)a と置くと, 当然 mx = mra = m((n/m)a) = (m×n/m)a = na となって欲しい。 最初の等号以外は r が正の整数ならば上記で述べたように成立する性質である。 そこで r = n/m を前のようにして
x = ra = (n/m)a ⇔ mx = na
と定義する (A ⇔ B は 「A と B とが論理的に同じ意味」 という意味)。 この mx = na の左辺の解釈は 「x と向きが同じで長さが m 倍」 であり, 右辺の解釈は 「a と向きが同じで長さが n 倍」 である。 このことから先ず 「a と x とは向きが同じ」 であり, 長さに関する性質から |mx| = m|x|, |na| = n|a| であるから, m|x| = n|a|, 即ち |x| = (n/m)|a| = r|a|. よって次のことが分かる。
r, s が正の有理数の時
ra と a とは向きが等しい。
|ra| = r|a|.
r(a + b) = ra + rb,
[scalar 分配法則]
r(sa) = (rs)a, [scalar 乗法の結合法則]
(r + s)a = ra + sa. [vector 分配法則]
例えば scalar 分配法則は r = n/m を規約分数として
m×左辺 = mr(a + b) = n(a + b)
= na + nb,
m×右辺 = m(ra + rb) = mra + mrb
= na + nb
となって, 確かに成り立つ。 その他も同様。 尚, r = n/m = n'/m' が規約分数でないとき (つまり n ≠ n', m ≠ m' の時) でもちゃんと ra = (n/m)a = (n'/m')a になっていることもちゃんと確認した方がいい (つまり所謂 well-definedness の検証) のだが省略する。
このようにして, 更に連続的に定義して, 正の実数 α, β に対しても
αa と a は向きが等しい,
|αa| = α|a|,
α(a + b) = αa + αb,
[scalar 分配法則]
α(βa) = (αβ)a, [scalar 乗法の結合法則]
(α + β)a = αa + βa. [vector 分配法則]
が成り立つ。 (大分ごまかしたので厳密性には欠けているがご容赦願いたい。)
さて, 前にやったように a = OA として, k > 0 とするとき ka = OAk となるように点 Ak を定める。 すると 1 倍に関する定義より OA = a = 1a = OA1 で あるから, A1 = A であるべきことが分かる。 このようにして次の図を得る。
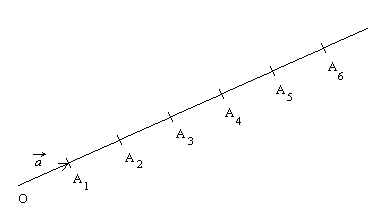
この図は数直線 (の半分) と良く似ている。 違うのは点が左側にあるからマイナスとはいえないのと, OA1 の長さは 1 とは限らないということくらいである。 図には描いていないが, 勿論この中には A1/2 とか, A2/3 とか A√2 とかいう点も含まれているのである。
そこで, これを完全に数直線の類似物として, OA1 の反対側に延長し, Ak の k < 0 の部分も考えたものが下の図である。
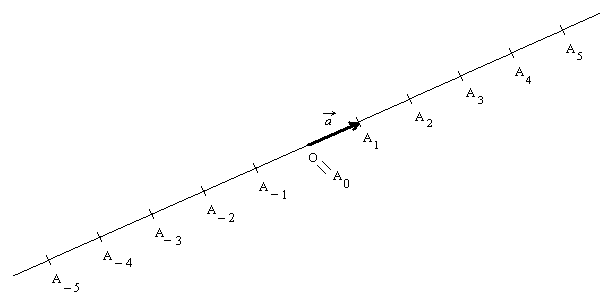
これを vector a の作る数直線と呼ぶことにしよう (ここの site の他では通用しない用語である)。 この直線は vector a の生成する直線 (line generated by a) とも呼ばれる (こちらは多分どこでも通用する)。
この図で点 O のところが A と対応がついていないと不自然であるから, 自然と O = A0 となるべきことが分かるであろう。 以下暫くこの vector a の作る数直線について考えていくことにする。
今や全ての実数 k に関し ka = OAk が成り立つように vector a の作る数直線を作ったのであるから, 0a = OA0 = A0A0 となっている。 この vector には
の二つの意味がある。 そこで
[定義]
始点と終点の一致した vector のことを零ベクトル zero vector といい, 0 と書く。 即ち 0 = 0a = AA (= BB = CC = …). 但し, 今後紛れのない限りにおいては只 0 と書いて zero vector を意味することにする。
さて, 0 も vector であるから, 向きと長さがあると考えられる。 長さについては上記の定義から |0| = |AA| = 0 であることには異論がないであろう。 ところが向きについては, かってな向きを持つ二つの vectors a, b に対して 0 = 0a = 0b であるから, どっちを向いているとも決め難い。
そこで, 0 は (その時必要な) 任意の方向を向いていると定める (zero vector の向きについては考えない, とする立場もある)。
Zero vector の持つ最も重要な性質は
a + 0 = 0 + a = a
である。 証明するために a = AB と置くと,
a + 0 = AB + BB = AB
= a,
0 + a = AA + AB = AB =
a.
このことを 0 は 「vectors の作る加法的可換半群の単位元 unit, idntity である」 といい, それ故 vectors は加法によって 「単位元を持つ可換半群を作る」 といわれる。
さて再び ka = OAk に戻ってもらおう。 今, この式は全ての実数 k で成立していると考えているので, 特に k = -1 の時を考えると
-1a = OA-1 = A0A-1
である。 この (右辺の) vector は A0A-1 = A1A0 であるから, a と大きさが等しく, 向きが正反対である。 そして, -1a は普通 -a と書きたくなるであろう。 そこで次のように定義する。
[定義]
Vector a と大きさが等しく, 向きが正反対の vector を a の逆ベクトルといい, -a と書く。
よって, -1a = -a であるが, -(-a) = a であることも分かるだろう (向きが逆のその又逆だから)。
逆 vector に関する最も重要な性質は
a + (-a) = (-a) + a = 0
である。 証明は a = OA と置くと, 定義から -a = -OA = AO であるから,
a + (-a) = OA + AO =
OO = 0,
(-a) + a = AO + OA =
AA = 0.
実は逆 vector というのは上記の性質を満たす唯一の vector である。 というのも, もし a + a' = a' + a = 0 とすると a' = a' + 0 = a' + a + (-a) = -a となるからである。 この性質から, -a は a の加法の逆元 inverse element, inverse であると言われる。 逆元と単位元を持つ半群のことを群 group というので, vectors は加法について可換群 commutative group, abelian group を作るという。
さて, 逆 vector を用いて, 負の数倍を定義しよう。 k > 0 とするとき
(-k)a = -(ka) = k(-a)
と定義する。 勿論, この式自体は k ≦ 0 でも成立している。 又これは (-k)a = A0A-k とも一致している。 この定義から k > 0 に対し
(-k)a は a と向きが正反対,
|(-k)a| = k|a|
であることが分かる。
この page の最後に実数倍について纏めておこう。
ここに表れ, 又 vector a の作る数直線にも示されているように, 実数倍は scale (スケール) を定めていると考えられるので, vector に対し, 実数を scalar (スカラー) という。 スカラー倍 (scalar multiplication) に対し, 次のことが成立している。
尚, 余り当面使わないが, scalar が実数の時には
aα = αa
としておく。