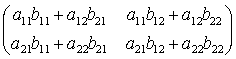 =
(aj1b1k + aj2b2k)
=
(aj1b1k + aj2b2k)集合 A, B, C と, 写像 f: A→B, g: B→C が与えられているとき x ∈ A に対し
(g°f)(x) = g(f(x))
で定まる写像 g°f: A→C を f と g の合成写像 composition という。
合成写像の表記の仕方は著者によって著しく違う。 上記のものが一番一般的だが gf と書いてしまう場合, (fg)(x) = g(f(x)) と逆順になっているもの, xfg = g(f(x)) という形に表記するものなどまちまちである。
もしも f も g も共に一次変換ならば, g°f も一次変換となり, これを f と g の合成変換と呼ぶ。 実際
(g°f)(kx + my)
= g(f(kx + my))
= g(kf(x) +
mf(y))
= kg(f(x)) + mg(f(y))
= k(g°f)(x) + m(g°f)(y).
以下同様にして次のことが確かめられる。 但し I は恒等変換である。
I°f = f°I
= f,
0°f = f°0
= 0,
(f°g)°h
= f°(g°h),
(f + g)°h = f°h
+ g°h,
f°(αg) = (αf)°g
= α(f°g).
さて次に, f を表す行列を A = (ajk), g を表す行列を B = (bjk) として f°g を表す行列を考えよう。
(x', y') = g(x, y), (x'', y'') = f(x', y') (= (f°g)(x, y))
とすると, A, B の決め方から
x' = b11x + b12y,
y' = b21x + b22y;
x'' = a11x' + a12y',
y'' = a21x' + a22y'
となる。 上の二組を下の二組に代入すると
x'' = a11(b11x + b12y) + a12(b21x + b22y)
= (a11b11 + a12b21)x + (a11b12
+ a12b22)y,
y'' = a21(b11x + b12y) + a22(b21x + b22y)
= (a21b11 + a22b21)x + (a21b12
+ a22b22)y
であるから, f°g を表す行列は
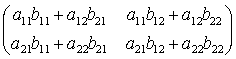 =
(aj1b1k + aj2b2k)
=
(aj1b1k + aj2b2k)
で定まる。 この行列を A と B の積 product といい AB と書く。 即ち
(ajk)(bjk) = (ajd)(bdk) = (aj1b1k + aj2b2k).
つまり, 前の方の行列の行が, 積の行を決めて, 後ろの方の行列の列が, 積の列を決定している (標語的に言えば行列の積だから 「行」 掛ける 「列」 だというわけである)。 真ん中の所を見ると d のところを 1, 2 と変えて和をとったものになっている。 この d は和をとるための添字だと考えられ, これを dummy index (無効添字) と呼ぶ。
この定義から, この page の上半分に対応して, 次の各々が対応する。 但し I2 は二次単位行列である。
I2A = AI2 = A,
0A = A0 = 0,
(AB)C = A(BC),
A(B + C) = AB + AC,
(A + B)C = AC + BC,
A(αB) = (αA)B = α(AB).
この中で一番大事なのは上から三番目の結合法則である。 これだけを確認しておこう。 今 A = (ajk), B = (bjk), C = (cjk) とするとき, 定義によって
(AB)C = (aj1b1k + aj2b2k)(cjk)
= (aj1b1d + aj2b2d)(cdk)
= ((aj1b11 + aj2b21)c1k +
(aj1b12 + aj2b22)c2k)
= (aj1b11c1k + aj2b21c1k
+ aj1b12c2k + aj2b22c2k),
A(BC) = (ajk)(bj1c1k + bj2c2k)
= (ajd)(bd1c1k + bd2c2k)
= (aj1(b11c1k + b12c2k) + aj2(b21c1k + b22c2k))
= (aj1b11c1k + aj1b12c2k
+ aj2b21c1k + aj2b22c2k).
従って証明された。
もしかすると, 分配法則 A(B + C) = AB + AC, (A + B)C = AC + BC はどちらか一方で良いと思った人がいるかもしれない。 しかし実は f°g と g°f は一般には等しくない (等しくないことが多い, 等しいことは稀である)。 従って一般には AB と BA は等しくない (可換でない, 非可換である)。 実際
(ajk)(bjk) = (ajd)(bdk) = (aj1b1k + aj2b2k)
と
(bjk)(ajk) = (bjd)(adk) = (bj1a1k + bj2a2k) = (a1kbj1 + a2kbj2)
は式の上で違っている (具体的な行列で確かめてみよ)。
更に AB = 0 であっても A ≠ 0, B ≠ 0 である場合がある。 もしも
A ≠ 0, B ≠ 0, AB = 0
が同時に成り立つとき, このような A と B を零因子 zero divisor であるという (つまり 0 の約数という意味である)。
例:
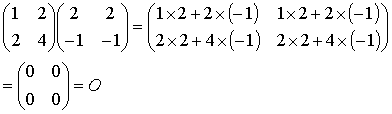
行列の定義は良くみてみると分かるが
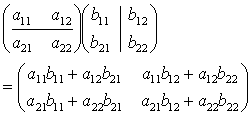
というように, 前の行列を行に, 後ろの行列を列に分割して考えると
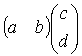 = ac + bd
= ac + bd
が成立するように, (第 j 行)×(第 k 行) = 第 (j, k) 成分 となっていることが分かる。 この最後の式を hint にして
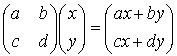
と定める。 即ち一次変換 f を表す行列を A とするとき, f は
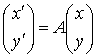
と書ける。 これを一次変換 f の行列表現という。