Sunday, 17th January, 2010.
13:30 -- 14:30 (1hr)
平均 57.12
注:
第一問, 第二問は必答。
第三問から第六問のうちから二問選択。
計四問を解答。
第一問 (必答 30 点)
[1] 連立方程式
(*) xy = 128 …………………………… (1)
1/log2x + 1/log2y = 7/12 ………… (2)
を満たす正の実数 x, y を求めよう。 但し, x ≠ 1, y ≠ 1 とする。 (1) の両辺で 2 を底とする対数を採ると
log2x + log2y = [ ア ]
が成り立つ。 これと (2) より
(log2x)(log2y) = [ イウ ]
である。
従って, log2x, log2y は二次方程式
t2 - [ エ ]t + [ オカ ] = 0 ………… (3)
の解である。 (3) の解は t = [ キ ], [ ク ] である。 但し, [ キ ], [ ク ] は解答の順序を問わない。 よって, 連立方程式 (*) の解は[2] 0 < θ < π/2 の範囲で
sin 4θ = cosθ ……………………(1)
を満たす θ と sinθ の値を求めよう。
一般に, すべての x について
cos x = sin([ シ ] - x)
である。 [ シ ] に当てはまるものを, 次の 0 から 2 の内から一つ選べ。
0 π
1 π/2
2 -π/2
となる。 従って, sin 4θ = sin([ シ ] - θ) となり, 0 < θ < π/2
の範囲で 4θ, [ シ ] - θ の採り得る値の範囲を考えれば,
4θ = [ シ ] - θ 又は 4θ = π - ([ シ ] - θ) となる。
よって (1) を満たす θ は θ = π/[ ス ] 又は θ = π/[ セソ ] である。
sin(π/[ ス ]) = [ タ ]/[ チ ] である。 sin(π/[ セソ ]) の値を求めよう。 (1) より
[ ツ ]sin 2θ cos 2θ = cosθ
となり, この式の左辺を二倍角の公式を用いて変形すれば
([ テ ]sin θ - [ ト ]sin3θ)cosθ = cosθ
となる。 ここで cosθ > 0 であるから
[ ト ]sin3θ - [ テ ]sin θ + 1 = 0 ……………………(2)
が成り立つ。 sinθ = [ タ ]/[ チ ] は (2) を満たしている。 θ = π/[ セソ ] とすると sinθ≠ [ タ ]/[ チ ] であるから
[ ナ ]sin2θ + [ ニ ]sinθ - 1 = 0
となる。 ここで, sin(π/[ セソ ]) > 0 より
sin(π/[ セソ ]) = ([ ヌネ ] + √[ ノ ])/[ ハ ]
である。
第二問 (必答 30 点)
k を実数とし, 座標平面上に点 P(1, 0) を採る。 曲線
y = -x3 + 9x2 + kx
を C とする。
(1) 点 Q(t, -t3 + 9t2 + kt) に於ける曲線 C の接線が P を通るとすると
-[ ア ]t3 + [ イウ ]t2 - [ エオ ]t = k
が成り立つ。
p(t) = -[ ア ]t3 + [ イウ ]t2 - [ エオ ]t
と置くと, 函数 p(t) は t = [ カ ] で極小値 [ キク ] を採り, t = [ ケ ] で極大値 [ コ ] を採る。
従って, 点 P を通る曲線 C の接線の本数が丁度二本となるのは, k の値が [ サ ] 又は [ シス ] の時である。 又, 点 P を通る曲線 C の接線の本数は k = 5 の時 [ セ ]本, k = -2 の時 [ ソ ] 本, k = -12 の時 [ タ ] 本となる。
(2) k = 0 とする。 曲線
y = -x3 + 6x2 + 7x
を D とする。 曲線 C と D の交点の x 座標は [ チ ] と[ ツ ]/[ テ ] である。
-1 ≦ x ≦ 2 の範囲に於いて, 二曲線 C, D 及び二直線 x = -1, x = 2 で囲まれた二つの図形の面積の和は [ トナ ]/[ ニ ] である。
第三問 (選択 20 点)
自然数の列 1, 2, 3, 4, ... を, 次のように分ける。
1 | 2, 3, 4, 5 | 6, 7, 8, 9, 10, 11, 12 | …
第一群 第二群 第三群
ここで, 一般に第 n 群は (3n - 2) 個の項からなるものとする。 第 n 群最後の項を anで表す。
(1) a1 = 1, a2 = 5, a3 = 12, a4 = [ アイ ] である。
an - an - 1 = [ ウ ]n - [ エ ] (n = 2, 3, 4, ...)
が成り立ち
an = ([ オ ]/[ カ ])n[ キ ] - ([ ク ]/[ ケ ])n (n = 1, 2, 3, ...)
である。
よって, 600 は, 第 [ コサ ] 群の小さい方から [ シス ] 番目の項である。
(2) n = 1, 2, 3, ... に対し, 第 (n + 1) 群の小さい方から 2n 番目の項を bn であらわすと
bn = ([ セ ]/[ ソ ])n[ タ ] + ([ チ ]/[ ツ ])n
であり
1/bn = ([ テ ]/[ ト ])(1/n - 1/(n + [ ナ ])) (n = 1, 2, 3, ,,,)
が成り立つ。 これより
Σk = 1n (1/bk) = [ ニ ]n/([ ヌ ]n + [ ネ ])
となる。
第四問 (選択 20 点)
本問では vectors はすべて太字斜体を用いる。
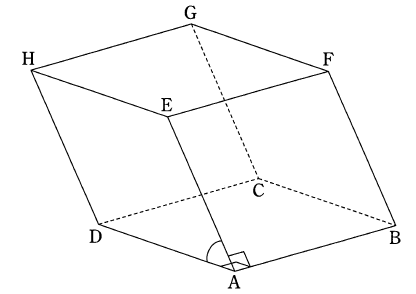
二つずつ平行な三組の平面で囲まれた立体を平行六面体という。 辺の長さが全て 1 の平行六面体 ABCD-EFGH があり, ∠EAB = ∠DAB = π/2, ∠EAD = π/3 である。 AB = p, AD = q, AE = r と置く。

0 < a < 1, 0 < b < 1 とする。 辺 AB を a : (1 - a) の比に内分する点を X, 辺 BF を b : (1 - b) の比に内分する点を Y とする。 点 X を通り直線 AH に平行な直線と辺 GH との交点を Z とする。 三角形 XYZ を含む平面を α とする。
(1) p・q = p・r = [ ア ], q・r = [ イ ]/[ ウ ] である。 ベクトル XY は, a, b, p, r を用いて XY = (1 - [ エ ])p + [ オ ]r と表される。
EC・XZ = [ カ ] である。
(2) 直線 EC と平面 α が垂直に交わるとし, 交点を K とする。 EC が三角形 XYZ の二辺と垂直であることから, [ キ ]a + b = [ ク ] が成り立つ。
以下では b = 1/2 とする。 この時 α = [ ケ ]/[ コ ] である。 EK を実数 c を用いて EK = cEC と表すと, AK = AE + cEC である。 一方, 点 K は平面 α 上にあるから, AK は実数 s, t を用いて
AK = AX + sXY + tXZ
= ((1/[ サ ])s + [ ケ ]/[ コ ])p + tq +
((1/[ シ ])s + t)r
と表される。 これらより, c = [ ス ]/[ セ ] である。 よって, 点 E と平面 α との距離 |EK| は [ ソ ](√[ タ ])/[ チ ] となる。
第五問 (選択 20 点)
次の表は, 高等学校のある部に入部した二十人の生徒について, 右手と左手の握力 (単位 kg) を測定した結果である。 測定は十人ずつの二つのグループについて行われた。 但し, 表中の数値は全て正確な値であり, 四捨五入されていないものとする。
|
第一グループ |
第二グループ |
|||||||
| 番号 | 右手の 握力 |
左手の 握力 |
左右の 握力の 平均値 |
番号 | 右手の 握力 |
左手の 握力 |
左右の 握力の 平均値 |
|
|
1 |
50 |
49 |
49.5 |
11 |
31 |
34 |
32.5 |
|
| 平均値 |
A |
44.5 |
44.75 |
平均値 |
43.0 |
D |
41.25 |
|
| 中央値 |
46.5 |
46.0 |
中央値 |
45.0 |
40.5 |
|||
|
分散 |
29.00 |
27.65 |
分散 |
41.00 |
26.25 |
|||
以下, 小数の形で解答する場合は, 指定された
(1) 第一グループに属する 10 人の右手の握力について,
平均値 A は [ アイ ].[ ウ ] kg である。
又, 20 人全員の右手の握力について平均値 M は [ エオ ].[ カ ] kg,
中央値は [ キク ].[ ケ ] kg である。
(2) 右手の握力について, 20 人全員の平均値 M からの偏差の 2 乗の和を, 二つのグループそれぞれについて求めると, 第一グループでは [ コサシ ] であり, 第二グループでは 420 である。 従って, 20 人全員の右手の握力について, 標準偏差 S の値は [ ス ].[ セ ] kg である。
(3) t を正の実数とする。 20 人全員の右手の握力の平均値 M と標準偏差 S を用いて,
M - tS より大きく M + tS より小さい範囲を考える。
20 全員の中で, 右手の握力の値がこの範囲に入っている生徒の人数を N(t) とする時,
N(1) = [ ソタ ] であり,
N(2) = [ チツ ] である。
(4) 第二グループに属する 10 人の左手の握力について, 平均値 D は [ テト ].[ ナ ] kg であり, 中央値が 40.5kg であるから, B の値は [ ニヌ ] kg, C の値は [ ネノ ] kg である。 但し, B の値は C の値より大きいものとする。 これより, E と F の値も定まる。
(5) 20 人の各生徒について,
右手と左手の握力の平均値と, 右手と左手の握力の差の絶対値を求めた。
握力の平均値については,
最初にあげた表の 「左右の握力の平均値」 の列に示している。
握力の平均値を横軸に,
握力の差の絶対値を縦軸に採った相関図 (散布図) として適切なものは [ ハ ] であり,
相関係数の値は [ ヒ ] に最も近い。
従って, この 20 人については, [ フ ]。
[ ハ ] に当てはまるものを,
次の 0 〜 3 のうちから一つ選べ。

[ ヒ ] に当てはまるものを, 次の 0 〜 4 のうちから一つ選べ。
0 -0.9
1 -0.5
2 0.0
3 0.5
4 0.9
[ フ ] に当てはまるものを, 次の 0 〜2 のうちから一つずつ選べ。
0 握力の平均値が増加する時, 握力の差の絶対値が増加する傾向が認められる
1 握力の平均値が増加する時, 握力の差の絶対値が増加する傾向も減少する傾向も認められない。
2 握力の平均値が増加する時, 握力の差の絶対値が減少する傾向が認められる
第六問 (選択 20 点)
自然数 N を三つの自然数 a, b, c の和として表す方法の総数を求める。
但し, a, b, c は a ≦ b ≦ c を満たすとする。
次のように考えよう。
先ず, a の採り得る値の範囲を求め, 次に, その範囲にある a の各値について,
a + b + c = N
となる自然数 b, c (a ≦ b ≦ c) の組を考える。
(1) a ≦ b ≦ c より, A のとり得る値は N/[ ア ] 以下の全ての自然数である。
(2) N = 20 とする。 この時, a のとり得る最大の数は [ イ ] であり, 更に, a = 3 の時, b, c (3 ≦ b ≦ c) の組は全部で [ ウ ] 個である。
(3) 自然数 N を三つの自然数 a, b, c の和として表す方法の総数を求める為, 以下のような〔プログラム〕を作成した。 但し INT (X) は X を超えない最大の整数を表す函数である。
〔プログラム〕
100 INPUT N
110 LET X = 0
120 FOR A = 1 TO INT(N/[ ア ])
130 LET [ エ ]
140 NEXT A
150 PRINT "N = "; N; "の時, 総数は "; X; " 通りである"
160 END[ エ ] に当てはまるものを, 次の 0 から 5 の中から一つ選べ。
0 X = X + 1
1 X = X + INT(A/2) - 1
2 X = X + A + 3
3 X = X + 2*INT(A/2) + 3
4 X = X + INT((N - A)/2) - 2
5 X = X + INT((N - A)/2) - A + 1
〔プログラム〕を実行して N に 13 を入力した時, 130 行は [ オ ] 回実行され, 150 行で出力される X の値は [ カキ ] である。
(4) 一般に, 三つの正の数について, どの二つの数の和も残りの数より大きければ, それらを三辺の長さとする三角形が存在する。 逆に, 全ての三角形に於いて, どの二辺の長さの和も残りの一辺の長さより大きい。
この事実を用いて, 自然数 N を三角形の三辺の長さとなり得る三つの自然数 a, b, c (a ≦ b ≦ c) の和として表す方法をすべて列挙し, その総数を求める。 その為には, (3) の〔プログラム〕の 130 行を削除して, 次の 131 行から 137 行を追加すれば良い。
131 FOR B = [ ク ]
132 LET C = [ ケ ]
133 IF [ コ ] THEN
134 PRINT "("; A; ", "; B; ", "; C; ")"
135 LET [ サ ]
136 END IF
137 NEXT B[ ク ] に当てはまるものを, 次の 0 から 5 の中から一つ選べ。
0 1 TO INT(N/2)
1 1 TO INT((N - A)/2)
2 A TO N
3 A TO N - 1
4 A TO INT((N - A)/2)
5 A TO INT((N - A)/2) + 1
[ ケ ] に当てはまるものを, 次の 0 から 5 のうちから一つ選べ。
0 B
1 B + A
2 B - A
3 N - B
4 N - A - B
5 N + A - B
[ コ ] に当てはまるものを, 次の 0 から 5 のうちから一つ選べ。
0 A < B + C
1 B < A + C
2 C < A + B
3 A < B + C + 1
4 B < A + C + 1
5 C < A + B + 1
[ サ ] に当てはまるものを, 次の 0 から 5 のうちから一つ選べ。
0 X = X + INT(N/2)
1 X = X + INT(N/3)
2 X = X + INT(A/2) + 1
3 X = X + A - 1
4 X = X + A
5 X = X + 1
変更後のプログラムを実行して, N に 13 を入力した時, 150 行で出力される X の値は [ シ ] である。
解答へ。
センター試験の目次に戻る。