第一問 (20 点)
[1] AB = 1/(((1 + √6) + √3)((1 + √6) -
√3))
= 1/((1 + √6)2 - 3) (2 点)
= 1/(7 +
2(√6) - 3) = 1/(4 + 2√6)
= 1/(2(2 + √6)) = ((√6 - 2)/(2(6 - 4)))
= ((√6) - 2)/4. (3 点)
1/A + 1/B = 1 + (√3) + (√6) + 1 - (√3) + √6
= 2
+ 2√6. (2 点)
1/A + 1/B = (A + B)/(AB) なので
A + B = AB(1/A + 1/B) = ((√6 - 2)/4)・2(1 +
√6) = (6 - 2 - √6)/2
= (4 - √6)/2. (3 点)
教科書 level 驚くべき簡単さ。 これが出来ないようではもうお終い。
[2] 以下では否定の記号として`p の代わりに ¬p と書くことにする。
(1) ¬(p or q) ⇒ ¬r 即ち (¬p & ¬q) ⇒ ¬r だから 1. (3 点)
(2) p or q ⇒ r とは
「三つの内角がすべて異なっているか直角三角形ではない三角形 ⇒ 45°の内角は一つもない」
の反例は,
三つの内角がすべて異なっていて 45°の内角が少なくとも一つあるものと, 直角三角形ではないが 45°の内角があるものなので 1
と 4. (各 2 点)
(3) (2) より 「p or q ⇒ r」 は偽である。
一方 「r ⇒ p or q」 とは 「45°の内角が一つもない ⇒
三つの内角がすべて異なる か 直角ではない三角形」
これの対偶は 「直角二等辺三角形 ⇒ 45°の内角がある」 だから真。
従って, 2. (3 点)
(3) が少しややこしくて難しいか。
(1) は基本問題。
第二問 (25 点)
P(-8 + 2t, 8 - 2t), Q(t, 10t) である。
P = O だから -8 + 2t = 8 - 2t = 0. 即ち t =
4. (3 点)
(1) P'(-8 + 2t, 0), Q'(t, 0).
△OPP' も △OQQ' も共に直角三角形なので
S = (8 - 2t)2/2 + t・10t/2
= 2(t - 4)2 + 5t2
= 7t2 - 16t + 32.
(3 点)
= 7(t2 - (16/7)t) + 32
= 7(t - 8/7)2 - 64/7 + 32
= 7(t
- 8/7)2 - 32・2/7 + 32・7/7
= 7(t - 8/7)2 + 32・5/7
= 7(t - 8/7)2 + 160/7.
より S は t = 8/7 で最小値 160/7 を採る。 (各 3 点)
区間 I: a ≦ t ≦ a + 1 とする。
(i) S が t = 8/7 で最小となるということは a ≦ 8/7 ≦ a + 1 であるから
1/7
≦ a ≦ 8/7. (3 点)
(ii) S が t = a (区間 I の左端) で最大ということは, t = 8/7 が区間 I の中央より右ということだから
a + 1/2
≦ 8/7 即ち a ≦ 8/7 - 1/2 = (16 - 7)/14 = 9/14.
(3 点)
(2) O を通る二次函数が y = 2x2 を平行移動したものだとすれば, それは
y = -2x2 + bx
という形をしている。 二点 P, Q を通るので
8 - 2t = 2(-8 + 2t)2 + b(-8 + 2t)
10t = 2t2 + bt.
下の方の式から 2t2 - 10t + bt = 0.
t > 0 だから 2t = 10 - b 即ち t = (10 - b)/2 で
0 < t < 4 より 0 < 10 - b < 8. つまり
-10 < -b < -2 即ち 2 < b < 10.
2t = 10 - b を上の方の式 (P を通る条件の式) に代入して
8 - (10 - b) = 2(-8 + 10 - b)2
+ b(-8 + 10 - b)
-2 + b = 2(2 - b)2 + b(2 - b).
b > 2 なので
1 = 2(2 - b) - b
= 2b - 4 - b
= b - 4
従って b = 5. (適)
故に t = (10 - b)/2 = 5/2 (3 点) の時で, この時
y = 2x2 + 5x = 2(x2 + (5/2)x) = 2((x + 5/4)2
- 25/16) = 2(x + 5/4)2 - 25/8
だから
x 軸方向に -5/4, y 軸方向に -25/8 平行移動する。 (各 2 点, 計 4 点)
定番だが (1) (ii) とか (2) の置き方とかに慣れてないと大変かもしれない。
(2)
は効率良い計算を普段から心がけておくことが必要であろう。
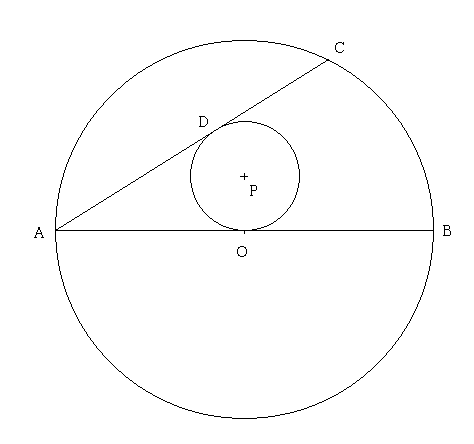
第三問 (30 点) 図を描きながらやること。
△APO で三平方の定理より
AP =√(32 + 12) = √10. (3 点)
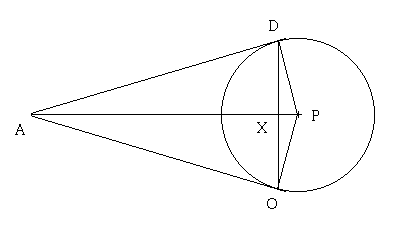
AD = AO = 3 で,
AP と OD の交点を X とすると
△AOP ∽ △OXP なので
OX : AO = OP : AP
OX = AO・OP/AP
OD = 2AO・OP/AP
= 2・3・1/√10
= 2・3(√10)/10
= 3(√10)/5. (3 点).
更に (第二) 余弦定理より
cos∠OAD = (2OA2 - OD2)/(2OA2)
= 1 - OD2/(2OA2) = 1 - 36/(10・2・9)
= 1 - 1/5 =
4/5. (2 点).
Thales の定理より ∠ACB = ∠R だから
AC = AB cos∠OAD = 6・4/5 = 24/5. (2 点)
sin A = √(1 - cos2A) = 3/5 なので,
△ABC = (1/2)・6・(24/5)・(3/5) = 216/25. (3 点)
BC = AB sin A = 6・3/5 = 18/5.
S = (a + b + c)r/2 より
r = 2S/(a + b + c)
= 2・216/25/(6 + 24/5 + 18/9) = (216/5)/(15 + 12 + 9) = 72/(5・(5 + 4 + 9)) =
72/(5・12)
= 6/5. (3 点)
(1) RQ = AC - 2r = 24/5 - 2・6/5 = 12/5. (3 点)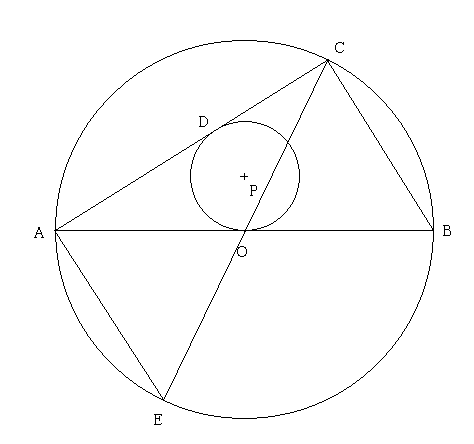
で RQ = 2r だから, この二つの円は外接。 即ち 2. (4 点)
(2) AQ = √((6/5)2 + (18/5)2)
= (6/5)√(1 + 32)
= 6(√10)/5. (2 点)
円 P, Q が共に線分 AB, AC に接していることから, 三点 A, P, Q は共線だから
PQ = AQ - AP
= 6(√10)/5 - √10
= (√10)/5. (3 点)
12/5 - 1 = 7/5 > (√10)/5 つまり
(円 P の半径) - (円 Q の半径) > 中心間の距離
だから円 P は円Q
の内部に含まれるので 2. (3 点)
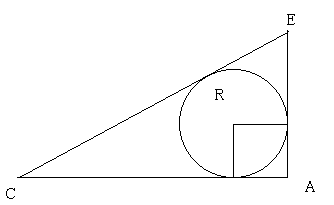
図を描きながらやらないと難しい。
円の半径と中心間距離の関係が出たのは初めてなので, 今後は要注意かも。
第四問 (25 点)
(1) 44 = 28 = 210 - 2 = 1024/4 = 256 (3 点)
(2) 4P4 = 4・3・2・1 = 24. (3 点)
(3) (i) 4C2 = 4・3/(2・1) = 6. (2 点)
(ii) 4C2 = 6. (2 点)
(iii) 6・6 = 36. (2 点)
(4) (i) 9 点は 4/256 = 1/64. (2 点)
3 点は
(3) より 36/256 = 9/64. (2 点)
(ii) 2 点は, (三回になるものの個数)・(一回になるものの個数)・(一回になる位の個数) で決まるので
4・3・4/256 = 3/16. (3 点)
1 点は
(二回になるものの個数)・(二回になる位の選び方)・(残り二つの決め方) で決まるので
4・4C2・3P2/256
= 4・6・3・2/256 = 9/16. (4 点)
(iii) 9・1/64 + 3・9/64 + 2・3/16 + 9/16 (9 + 27)/64 + (6 + 9)/16
=
36/64 + 15/16 = (9 + 15)/16 = 24/16 = 3/2 [点].
(2 点)
昨年に引き続き簡単だった。 ケアレスミスに気を付けて計算することが重要である。
今年の数学 I ・ A は簡単だった去年よりも更に簡単になった。
難しいとすれば図形の第三問だけ。 図形問題に慣れておくことが必要か。
ケアレスミスが致命的だったのではないかと思われる。
センター試験の目次に戻る。