
Sunday, 18th January, 2015.
11:20 -- 12:20 (1hr)
平均 61.27
第一問 (必答 20 点)
二次関数
y = -x2 + 2x + 2 ……… (1)
のグラフの頂点の座標は ([ ア ] , [ イ ]) である。 又
y = f(x)
は x の二次関数で, そのグラフは, (1) のグラフを x 軸方向に p, y 軸方向に q だけ平行移動したものであるとする。
(1) 下の [ ウ ], [ オ ] には, 次の 0 から 4 の内から当てはまるものを一つずつ選べ。 但し, 同じものを繰り返し選んでも良い。
0 >
1 <
2 ≧
3
≦
4 ≠
2 ≦ x ≦ 4 における f(x) の最大値が f(s) になるような p の値の範囲は
p [ ウ ] [ エ ]
であり, 最小値が f(2) になるような p の値の範囲は
p [ オ ] [ カ ]
である。
(2) 二次不等式 f(x) > 0 の解が -2 < x < 3 になるのは
p = [ キク ]/[ ケ ], q = [ コサ ]/[ シ ]
の時である。
(1) 次の に当てはまるものを, 下の 0 から 3 の内から一つ選べ。
p の否定`p は [ ク ] である。
0 m > k 又は n > k
1 m > k 且つ n > k
2 m ≦ k 且つ n ≦ k
3 m ≦ k 又は n ≦ k
(2) 次の から [ サ ] に当てはまるものを下の 0 から 3 の内から一つずつ選べ。
但し, 同じものを繰り返し選んでも良い。
(i) k = 1 とする。
p は q である為の [ ケ ]。
(ii) k = 2 とする。
p は r である為の。
p は q である為の [ ]。
0 必要十分条件である
1 必要条件であるが, 十分条件でない
2 十分条件であるが, 必要条件でない
3 必要条件でも十分条件でもない
第二問 (必答 15 点)
[1] 条件 p1, p2, q1, q2 の否定をそれぞれ ¬p1, ¬p2, ¬q1, ¬q2 と書く。 (ここは原文と変えてある)
(1) 次の [ ア ] に当てはまるものを, 下の 0 から 3 の内から一つ選べ。
命題 「(p1 且つ p2) ⇒ (q1 且つ q2)」 の対偶は [ ア ] である。
0 (¬p1 又は ¬p2) ⇒ (¬q1 又は ¬q2)
1 (¬q1 又は ¬q2) ⇒ (¬p1 又は ¬p2)
2 (¬q1
且つ ¬q2) ⇒ (¬p1 且つ ¬p2)
3
(¬p1 且つ
¬p2) ⇒ (¬q1 且つ ¬q2)
(2) 自然数 n に対する条件 p1, p2, q1, q2 を次のように定める。
p1: n は素数である。
p2: n + 2 は素数である。
q1: n
+ 1 は 5 の倍数である。
q2: n + 1 は 6 の倍数である。
30 以下の自然数 n の中で, [ イ ] と [ ウエ ] は
命題 「(p1 且つ p2) ⇒ (q1 且つ q2)」
の反例となる。
[2] △ABC に於いて, AB =3. BC = 5. ∠ABC = 120°とする。
この時, AC = [ オ ], sin∠ABC = (√[ カ ])/[ キ ] であり, sin∠BCA = [ ク ](√[ ケ ])/[ コサ ] である。
直線 BC 上に点 D を, AD = 3√3 且つ ∠ADC が鋭角, となるように取る。 点 P を線分 BD 上の点とし, △APC の外接円の繁ケ尾を R とすると, R の取り得る値の範囲は [ シ ]/[ ス ] ≦ R ≦ [ セ ] である。
第三問 (必答 30 点)
[1] ある高校三年生一クラスの生徒四十人について, ハンドボール投げの飛距離のデータを取った。 次の図 1 は, このクラスで最初に取ったデータのヒストグラムである。

(1) 次の [ ア ] に当てはまるものを, 下の 0 から 8 の内から一つ選べ,。
この四十人のデータの第 3 四分位数が含まれる階級は [ ア ] である。
0 5 m 以上 10 m 未満
1 10 m 以上 15 m 未満
2 15 m 以上 20 m 未満
3 20 m 以上 25 m 未満
4 25 m 以上 30 m 未満
5 30 m 以上 35 m 未満
6
35 m 以上 40 m 未満
7 40 m 以上 45 m 未満
8 45 m
以上 10 m 未満
(2) 次の [ イ ] から [ オ ] に当てはまるものを, 下の 0 から 5 の内から一つずつ選べ。 但し, [ イ ] から [ オ ] の解答の順序は問わない。
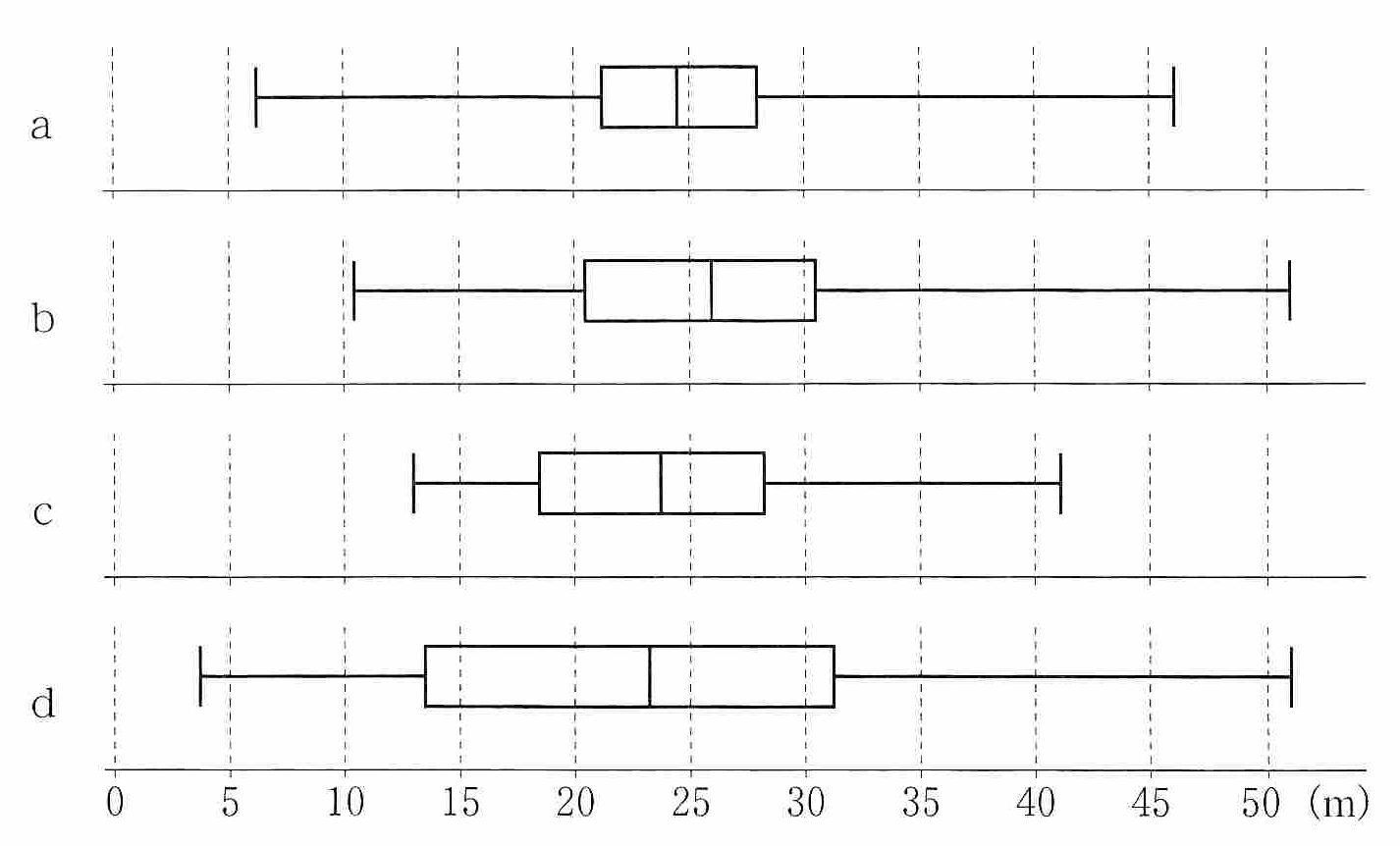
このデータを箱ひげ図にまとめた時, 図 1 のヒストグラムと矛盾するものは [ イ ], [ ウ ], [ エ ], [ オ ] である。

(3) 次の文章中の [ カ ], [ キ ] に入れるものとして最も適当なものを, 下の 0 から 3 の内から一つずつ選べ。 但し, [ カ ], [ キ ] の解答の順序は問わない。
後日, このクラスでハンドボール投げの記録を取り直した。 次に示した A から D は最初にとった記録から今回の記録への変化の分析結果を記述したものである。 a から d の各々が今回取り直したデータの箱ひげ図と異なる場合に 0 から 3 の組み合わせの内分析結果と箱ひげ図が矛盾するものは [ カ ], [ キ ] である。
0 A - a
1 B - b
2 C
- c
3 D - d
A: どの生徒の記録も下がった。
B: どの生徒の記録も伸びた。
C: 最初に取ったデータで上位 1/3 に入るすべての生徒の記録が伸びた。
D: 最初に取ったデータで上位 1/3 に入るすべての生徒の記録は伸び, 下位 1/3 に入るすべての生徒の記録は下がった。
[2] 或る高校二年生四十人のクラスで一人二回ずつハンドボール投げの飛距離のデータを取ることにした。 次の図 2 は, 一回目のデータを横軸に, 二回目のデータを縦軸にとった散布図である。 尚, 一人の生徒が欠席した為, 39 人のデータとなっている。

| 平均値 | 中央値 | 分散 | 標準偏差 | |
| 一回目のデータ | 24.70 | 24.30 | 67.40 | 8.21 |
| 二回目のデータ | 26.90 | 48.72 | 48.72 | 6.98 |
一回目のデータと二回目のデータの共分散: 54.30
(共分散とは一回目のデータの偏差と二回目のデータの偏差の積の平均である。)
次の [ ク ] に当てはまるものを下の 0 から 9 の内から一つ選べ。
一回目のデータと二回目のデータの相関係数に最も近い値は, [ ク ] である。
0 0.67
1 0.71
2 0.75
3 0.79
4 0.83
5 0.87
6 0.91
7 0.95
8 0.99
9 1.03
第四問から第六問は何れか二問を選択し, 解答しなさい。
第四問 (選択 20 点)
同じ大きさの五枚の正方形の板を一列に並べて, 図のような掲示板を作り, 壁に固定する。 赤色, 緑色, 青色のペンキを用いて, 隣り合う正方形同士が異なる色となるように, この掲示板を塗り分ける。 但し, 塗り分ける際には, 三色のペンキをすべて使わなければならないわけではなく, 二色のペンキだけで塗り分けることがあっても良いものとする。
(1) このような塗り方は [ アイ ] 通りある。
(2) 塗り方が左右対称となるのは, [ ウエ ] 通りある。
(3) 青色と緑色の二色だけで塗り分けるのは, [ オ ] 通りある。
(4) 赤色に塗られる正方形が三枚であるのは, [ カ ] 通りある。
(5) 赤色に塗られる正方形が一枚である場合について考える。
よって, 赤色に塗られる正方形が一枚であるのは, [ コサ ] 通りある。
(6) 赤色に塗られる正方形が二枚であるのは, [ シス ] 通りある。
第五問 (選択 20 点)
以下では, a = 756 とし, m は自然数とする。
(1) a を素因数分解すると
a = 2[ ア ]3[ イ ][ ウ ]
である。
a の所為の約数の個数は [ エオ ] 個である。
(2) √(am) が自然数となる最小の自然数 m は [ カキ ] である。 √(am) が自然数となる時, m はある自然数 k により, m = [ カキ ]k2 と表される数であり, その時の √(am) の値は [ クケコ ]k である。
(3) 次に, 自然数 k により [ クケコ ]k と表される数で, 11 で割った余りが 1 となる最小の k を求める。 一次不定方程式
[ クケコ ]k - 11l = 1
を解くと, k > 0 となる整数解 (k, l) の内, k が最小のものは, k = [ サ ], l = [ シスセ ] である。
(4) √(am) が 11 で割ると 1 余る自然数となる時, そのような自然数 m の中で最小のものは [ ソタチツ ] である。
第六問 (選択 20 点)
△ABC に於いて, AB = AC = 5, BC = √5 とする。 辺 AC 上に点 D を AD = 3 となるようにとり, 辺 BC の B の側の延長と △ABD の外接円との交点で B と異なるものを E とする。
CE・CB = [ アイ ] であるから, BE = √[ ウ ] である。
△ACE の重心を G とすると, AG = [ エオ ]/[ カ ] である。
AB と DE の交点を P とすると
DP/EP = [ キ ]/[ ク ] ……… (1)
である。
△ABC と △EDC に於いて, 点 A, B, D, E は同一円周上にあるので ∠CAB = ∠CDE で, ∠C は共通であるから
DE = [ ケ ]√[ コ ] ……… (2)
(1), (2) から, EP = ([ サ ]√[ シ ])/[ ス ] である。
解答へ。
センター試験の目次に戻る。