
[7π/6 rad]
7π/6 = 180 度× 7/6 = 210 度。 210 度 = 180 度 + 30 度。

前の時と同様に符号を考えると, 動径はいつも +, 横の線は x 軸と同じなので -, 楯の線は y 軸と同じなので, これも -. というわけで
sin 7π/6 = -1/2, cos 7π/6 = (-√3)/2 = -(√3)/2, tan 7π/6 = (-1)/(-√3) = 1/√3.
[5π/4 rad]
5π/4 = 180 度×5/4 = 225 度。 225 度 - 180 度 = 45 度。 図から

sin 5π/4 = -1/√2, cos 5π/4 = -1/√2, tan 5π/4 = -1/(-1) = 1.
[4π/3 rad]
4π/3 rad = 180度×4/3 = 240 度。240 度 - 180 度 = 60 度。 図から

sin 4π/3 = (-√3)/2 = -(√3)/2, cos 4π/3 = -1/2, tan 4π/3 = (-√3)/(-1) = √3.
[3π/2 rad]
3π/2 rad = 180度×3/2 = 270 度。 270 度 = 90度×3.

又 y 軸と重なってしまうので, π/2 の時のように, もうちょっとずらしたいい加減な図を描くと,

sin 3π/2 = -1/1 = 1, cos 3π/2 = 0/1 = 0. tan に関しては, π/2 に関して述べたように, 定義されない。
[5π/3 rad]
5π/3 rad = 180 度× 5/3 = 300 度。 360 度 - 300 度 = 60 度。

図のようにして
sin 5π/3 = (-√3)/2 = -(√3)/2, cos 5π/3 = 1/2, tan 5π/3 = (-√3)/1 = -√3.
[7π/4 rad]
7π/4 rad = 180 度× 7/4 = 315 度。 360 度 - 315 度 = 45 度。

図のようにして
sin 7π/4 = -1/√2, cos 7π/4 = 1/√2, tan = -1/1 = -1.
11π/6 rad = 180 度 × 11/6 = 330 度。 360 度 - 330 度 = 30 度。

というわけで図から
sin 11π/6 = -1/2, cos 11π/6 = (√3)/2, tan 11π/6 = -1/√3.
[2π rad]
2π rad = 360 度。 これで一周戻ってきたので 0 の時と同様に
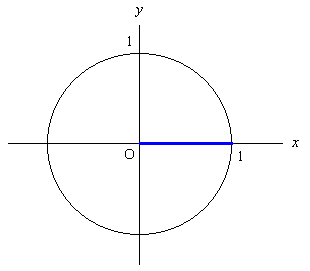
sin 2π = sin 0 = 0, cos 2π = cos 0 = 1, tan 2π = tan 0 = 0.
これで一周終わり。 お疲れさまでした (笑)