
先ず, 時刻 0 で原点を出発し, 一定の速度 v で運動する物体が, 時刻 x のときにいる位置 y を調べてみよう。 こういう運動を等速直線運動 --- 又は等速度運動 uniform motion --- というのであった。
これは --- 文字を使うところは除いて --- 小学生の知識で出来て y = vx になる。 単位を考えれば km/h に h を掛ければ距離になる --- 例の 「はじきの図」 でもいい。
じゃぁ, v が一定じゃなかったら ? っていうのが問題。 いちばん簡単な場合は v = ax (a は 0 でない定数)。 この場合は答えを知っているかもしれない。 でもどうしてそうなるか知ってる ? しかも, v = ax2 とかになったらどうなるか想像できる ?
そこで, y = vx について少し反省する。
時間に対する, 速度 v の変化のグラフを描く。 --- 変化のって言ったって, 変化しないから凄く単純なグラフになるんだけど (笑)。

時刻 x における位置 y が vx ということは, y は上の図でどこに現れているだろう ? わざとらしく色がついてるから分かるかな ? (笑) そう, 図の四角の面積になるんだよね。 この面積は丁度縦が v, 横が x だからその面積 y = vx. いいよね。
同様に考えると v = ax というように, v が時間変化を起こすときも, 時刻 x における位置 y はグラフが作る面積になるはずだ。
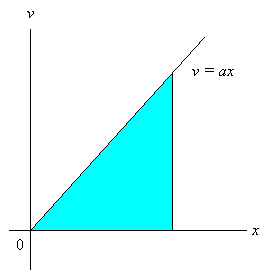
ということは, v = ax の場合には, 三角形の面積だから, 底辺 x 掛ける高さ v = ax を 2 で割るのだから, y = ax2/2 ということになる。
ついでだから言っておくと v = ax + b の場合は, 台形の面積になる。 次の教育課程で習ってくる高校生達は, 台形の面積の公式を知らないのだな...。 台形の面積の公式は (上底 + 下底) × 高さ ÷ 2 だってことを黙って使っちゃうと (笑), y = (b + (ax + b))x/2 = (ax + 2b)x/2 = ax2/2 + bx となる (名前に反して, 図では左が上底, 右が下底だよ)。 いいかな, これを物理 --- 理科の第一分野かな ? --- で習っているんだよ --- 但し a じゃなくて重力加速度 g で習っているはずだけど。
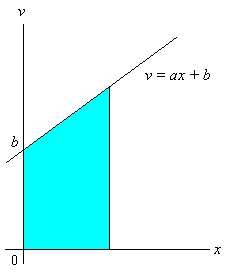
ここまではいいけど, じゃぁ v = ax2 だったりしたらどうなるの ? 今までの話の続きだと, 放物線と直線で囲まれる部分の面積を求めないといけないよね。

歴史的な話をすると, これの面積を求めるのは大変だった。 アルキメデスという大天才が紀元前にやっているけれど, ものすごく難しい。 今では誰でも簡単に求められるんだけどね (笑)。
ものの本に拠れば, 次のような表を書いて, しばらく考えさせると, クラスの中で一人くらいは分かるって言うんだけど, どうかね ? 分かる ? 僕はそれを読んだとき, 正直 「馬鹿言っちゃいけない, そんなに出来る奴がいたら苦労はしない」 っていったんだけどね ? 君は 「出来る」 人かな ? (笑)
| 速さ | 位置 (面積) |
| v | vx |
| ax | ax2/2 |
| ax2 | ? |
どう ? 分かった ? 分からなくてもいいよ。 とにかくここまでで分かってほしいのは, 速さから位置を求めるって問題は, グラフを描いて面積を求める問題と同じだってことさ。 次の問題はどうやったら面積が求まるのかってことね。