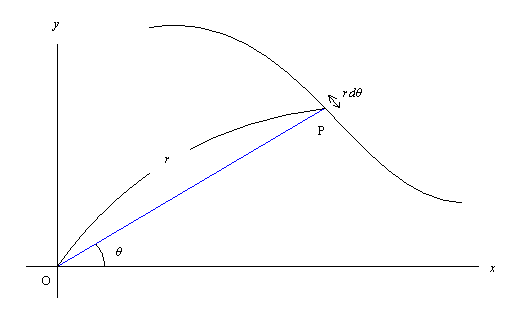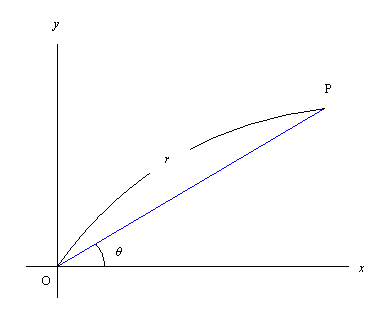
点の座標を表すのに, 直交座標系ではなくて, 極座標 polar coordinates と呼ばれる形式で表示をすることがある。 それは原点からの距離と, x 軸正の部分から計った角度 (それを通常偏角という) によって位置を表すものである。 原点からの距離を r, 偏角を θ とすると, 直交座標との関係は
x = r cos θ,
y = r sin θ
で表される。

さて, 或る図形がその偏角 θ (但し偏角は弧度法で計る) と原点からの距離 r との函数 r = g(θ) と表されているとき, その方程式を極方程式という。 この場合, 図のように薄い扇形を足し合わせていくことになる。 その面積は g(θ)2dθ/2 なので, 偏角が α から β 迄 (α < β) の間で与えられる部分の面積は
(1/2)∫αβ g(θ)2 dθ
で与えられることになる。