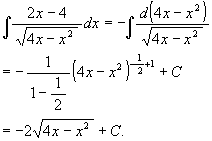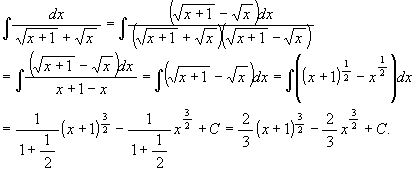
例: 積分定数 C に関してはいちいち断らない。

(1)

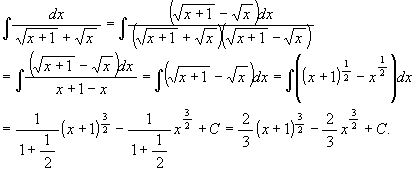
(2) .

これは t² = 2x + 1 と変数変換すると 2tdt = 2dx 即ち dx = tdt だから

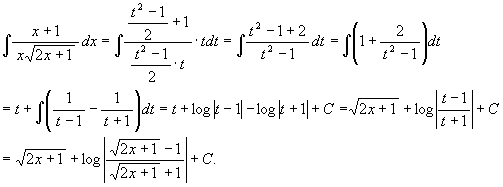
(3)

t² = 1 - x と置くと, 2tdt = -dx 即ち dx = -2tdt. よって

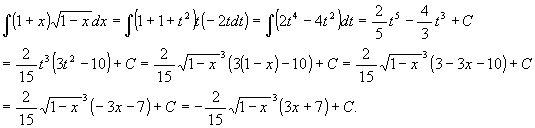
(4)

これは x の 1/2 乗と x の 1/3 乗が出てくるので, 2 と 3 の最小公倍数をとって

t⁶ = x と置くと, 6t⁵dt = dx だから

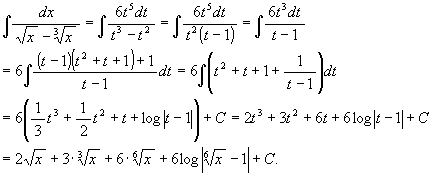
(5)

t² = 2x + 1 と置くと, 2tdt = 2dx, 即ち dx = tdt なので

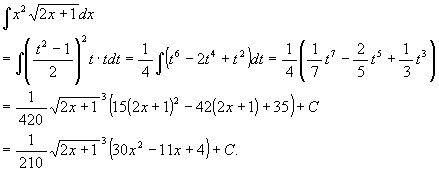
(6) a > 0 として .

x = a sin t, t ∈ [-π/2, π/2] と置くと, dx = a cos t dt, cos t ≧ 0 であるから

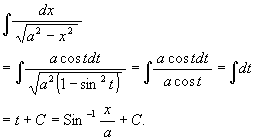
(7) a > 0 として .

x = a sin t, t ∈ [-π/2, π/2] と置くと, dx = a cos t dt, cos t ≧ 0 であるから (二倍角の公式を用いて)

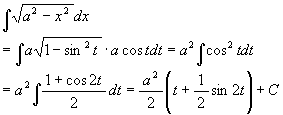
ここで a²sin 2t = 2a sin t×a cos t, より . 従って

やってみると分かるが はやっても無駄である。

(8)

[解 1] 上記のように x = sin t と置いてみると

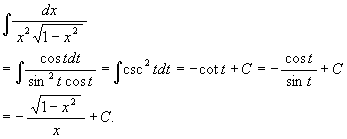
[解 2] 今度は と置いてみると 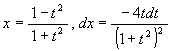だから

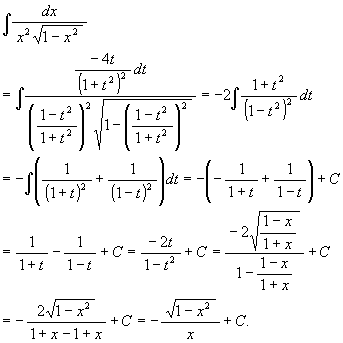
(9).

[1] (2) で述べたように, と置くと

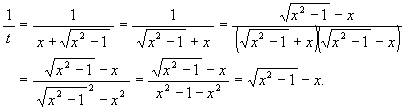
従って

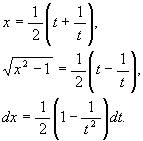
従って

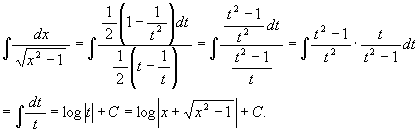
(10) 同様に と置くと を得る。

(11)

戻る