, a ≠ 0[1] F(x, y) は x, y に関する有理式とする。 これから考えるのは
, a ≠ 0
である。
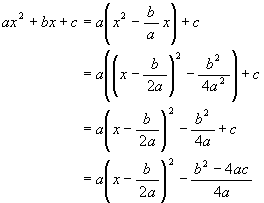
と変形できるから,
a > 0 の場合は 
と置くと, 
と変形できて, これは + のとき t = p tan θ と, - のとき t
= p sec θ と置くと上手くいく。
a < 0 の場合は, 同様に 
と置くと, 
と変形できて, これは t = p sin θ (或いは p cos θ)
と置くと上手くいく。
しかし, わざわざ三角函数を経由しなくても上手くいくことが分かっている。 以下その方法を解説する。
と置くと, y2
= ax2 + bx + c であるが, この二次曲線上にある (x0,
y0) 上を通る傾き t の直線 y = t(x - x0) + y0
は, (x0, y0) 以外の一点 P(x, y)
でこの同じ曲線と交わる。 従って, この点 P と傾き t
とが一対一に対応する。 代入して計算し x = φ(t), y = ψ(t)
と表されるとすれば, それは有理式で, 置換積分法によって
で積分できる。
(1) 特に y2 = ax2 + bx + c = a(x - α)(x - β) というように, 二つの相異なる実数 α, β によって因数分解されたとする。 このときは, 上記の (x0, y0) として特に (α, 0) を採用すると, これを通る傾き t の直線は y = t(x - α) と出来る。 即ち
t2(x - α)2 = a(x - α)(x - β)
t2(x - α) = a(x - β)
だから
という変換をすると上手くいく。
(2) ax2 + bx + c = 0 が実数解を持たない時は, 判別式 D = b2 -4ac < 0 であるから, 上記の変形を見ると積分の平方根の中が + であるためには a > 0 でなければならない。 平方根の中の二次式 ax2 + bx + c が実数解を持つか持たないかにかかわらず, a > 0 の場合は
言い換えると
という変形をすると上手くいく。
この場合は曲線 y2 = ax2 + bx + c
は双曲線と呼ばれる曲線で, 直線
はこの双曲線の漸近線に平行なので,
双曲線と直線の交点が只一つに定まり, 媒介変数 t
で表されるのである。
[2] 積分 
(ac ≠ 0) は,
t2 = ax + b と置けば, [1] の場合に帰結する。
更に一般に 
で α, β,
... は有理指数とする時, 積分
∫F(x, yα, yβ, ...)dx
は, 有理指数 α, β, ... の公分母
(つまり通分した時の分母) n を用いて 
で有理化できる。
[3] [二項微分の積分]
これは∫xm(axn+b)q dx という形の積分で, Newoton が研究したもの。 先ず t = xn と置くと, 定数倍を除いて
∫tp(at + b)q dt, p = (m + 1)/n - 1.
従って, p, q が有理数でしかも p, q 又は p + q が整数の場合には上手く行く。
先ず q が正の整数の場合は (at + b)q を展開するのが手っ取り早い --- 変換前でもそうだ。 q = 0 ならば何の問題もない。 従って q が負の整数の場合を考えると, この場合は p = h/k と既約分数で書くと, t = sk と変換すれば
k∫sh+k-1(ask + b)q ds
となる。 p が整数の場合は at + b の方を別の変数で変換すれば, 上記の場合に帰結する。 最後に p + q が整数の場合は 1/t = t-1 を変数にすればよい。
これらの場合の他は所謂初等函数にはできないということが Tschebyscheff (チェビシェフ) が Journal de Liouville (18), 1853 で証明している。
一寸ごたごたしたが, 二項微分の積分は最初の形で q 又は (m+1)/n 又は (m+1)/n + q の何れかが整数である場合に限って (初等函数への) 不定積分が出来る。
さて上記では積分計算が実行できる場合のみを扱ってきたが,
実は何でもかんでも出来るというのではない。 式 
で P(x) が平方因子を持たない三次又は四次の多項式の場合,
その積分は今まで我々の知るような簡単な函数にならない。
この場合の積分は楕円積分と呼ばれる。 又 deg P(x) > 4
の場合は超楕円積分と呼ばれる。 又,
互いに他の実数倍にはならないような一次式の平方根が,
三つ以上含まれる場合も同様の難しい積分になってしまう。
些か例が長くなったのでこちらへ。